Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 1 trang 32, 33 SGK Toán 12 tập 2 chương trình Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập hiệu quả, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Bài tập trong mục này tập trung vào các kiến thức quan trọng của chương trình, đòi hỏi các em phải có sự hiểu biết sâu sắc về lý thuyết và khả năng vận dụng linh hoạt vào thực tế.
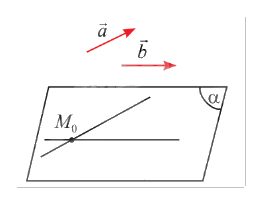
a) Cho vectơ (vec n) khác (vec 0). Qua một điểm ({M_0}) cố định trong không gian, có bao nhiêu mặt phẳng (left( alpha right)) vuông góc với giá của vectơ (vec n)?
Trả lời câu hỏi Vận dụng 1 trang 33 SGK Toán 12 Chân trời sáng tạo
Trong không gian \(Oxyz\), cho ba điểm \(A\left( {3;0;0} \right)\), \(B\left( {0;4;0} \right)\), \(C\left( {0;0;5} \right)\).
a) Tìm toạ độ của một cặp vectơ chỉ phương của mặt phẳng \(\left( {ABC} \right)\).
b) Tìm toạ độ của một vectơ pháp tuyến của mặt phẳng \(\left( {OAB} \right)\).
Phương pháp giải:
a) Chỉ ra 2 vectơ không cùng phương và có giá song song hoặc nằm trên mặt phẳng \(\left( {ABC} \right)\).
b) Chỉ ra 1 đường thẳng vuông góc với mặt phẳng \(\left( {OAB} \right)\), sau đó chọn 1 vectơ nằm trên mặt phẳng đó làm vectơ pháp tuyến của mặt phẳng \(\left( {OAB} \right)\).
Lời giải chi tiết:
a) Ta có \(\overrightarrow {AB} \left( { - 3;4;0} \right)\) và \(\overrightarrow {AC} \left( { - 3;0;5} \right)\) là hai vectơ không cùng phương và có giá nằm trong mặt phẳng \(\left( {ABC} \right)\). Vậy \(\overrightarrow {AB} \left( { - 3;4;0} \right)\) và \(\overrightarrow {AC} \left( { - 3;0;5} \right)\) là một cặp vectơ chỉ phương của mặt phẳng \(\left( {ABC} \right)\).
b) Ta thấy rằng \(A\left( {3;0;0} \right) \in Ox\), \(B\left( {0;4;0} \right) \in Oy\), \(C\left( {0;0;5} \right) \in Oz\).
Dễ dàng suy ra rằng \(OC \bot OA\) và \(OC \bot OB\), từ đó \(OC \bot \left( {OAB} \right)\).
Hơn nữa, vectơ \(\overrightarrow {OC} \left( {0;0;5} \right)\) có giá là đường thẳng \(OC\). Do đó \(\overrightarrow {OC} \left( {0;0;5} \right)\) là một vectơ pháp tuyến của mặt phẳng \(\left( {OAB} \right)\).
Trả lời câu hỏi Hoạt động 1 trang 32 SGK Toán 12 Chân trời sáng tạo
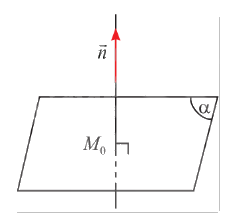
a) Cho vectơ \(\vec n\) khác \(\vec 0\). Qua một điểm \({M_0}\) cố định trong không gian, có bao nhiêu mặt phẳng \(\left( \alpha \right)\) vuông góc với giá của vectơ \(\vec n\)?
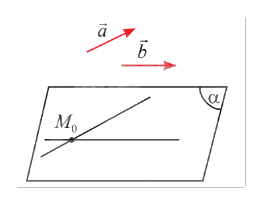
b) Cho hai vectơ \(\vec a\) và \(\vec b\) không cùng phương. Qua một điểm \({M_0}\) cố định trong không gian, có bao nhiêu mặt phẳng \(\left( \alpha \right)\) song song hoặc chứa giá của hai vectơ \(\vec a\) và \(\vec b\)?
Phương pháp giải:
Sử dụng các kiến thức về đường thẳng vuông góc mặt phẳng, đường thẳng song song với mặt phẳng đã được học ở các lớp dưới.
Lời giải chi tiết:
a) Với một điểm và một đường thẳng trong không gian, có duy nhất một mặt phẳng đi qua điểm và vuông góc với đường thẳng đó. Vậy có duy nhất một mặt phẳng \(\left( \alpha \right)\) đi qua điểm \({M_0}\) và vuông góc với giá của vectơ \(\vec n\).
b) Do hai vectơ \(\vec a\) và \(\vec b\) không cùng phương, giá của hai vectơ (lần lượt là \(a\) và \(b\)) không song song hay trùng nhau. Chọn đường thẳng \(a'\) sao cho \(a'\) song song hoặc trùng với \(a\) và \(a'\) cắt \(b\). Khi đó, có duy nhất một mặt phẳng \(\left( \beta \right)\) chứa \(a'\) và \(b\).
Nếu \({M_0} \in \left( \beta \right)\) thì mặt phẳng \(\left( \beta \right)\) là mặt phẳng duy nhất đi qua \({M_0}\) và song song hoặc chứa giá của hai vectơ \(\vec a\) và \(\vec b\).
Nếu \({M_0} \notin \left( \beta \right)\), thì trong không gian, tồn tại duy nhất mặt phẳng \(\left( \alpha \right)\) đi qua \({M_0}\) và song song với \(\left( \beta \right)\). Khi đó, \(\left( \alpha \right)\) song song hoặc chứa giá của hai vectơ \(\vec a\) và \(\vec b\).
Trả lời câu hỏi Thực hành 1 trang 33 SGK Toán 12 Chân trời sáng tạo
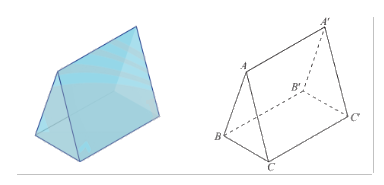
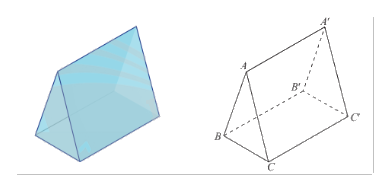
Một lăng kính có dạng hình trụ đứng có đáy là tam giác đều ở hình a được vẽ lại như hình b. Tìm một cặp vectơ chỉ phương và một vectơ pháp tuyến của mặt phẳng \(\left( {A'B'C'} \right)\).
Phương pháp giải:
Để xác định một cặp vectơ chỉ phương của mặt phẳng \(\left( {A'B'C'} \right)\), chỉ ra hai vectơ không cùng phương và có giá song song hoặc nằm trong mặt phẳng \(\left( {A'B'C'} \right)\).
Để xác định một vectơ pháp tuyến của mặt phẳng \(\left( {A'B'C'} \right)\), chỉ ra một đường thẳng vuông góc với \(\left( {A'B'C'} \right)\), sau đó chọn một vectơ có giá song song hoặc trùng với đường thẳng đó.
Lời giải chi tiết:
Ta thấy rằng \(\overrightarrow {A'B'} \) và \(\overrightarrow {A'C'} \) là hai vectơ không cùng phương và có giá nằm trong mặt phẳng \(\left( {A'B'C'} \right)\). Suy ra \(\overrightarrow {A'B'} \) và \(\overrightarrow {A'C'} \) là một cặp vectơ chỉ phương của mặt phẳng \(\left( {A'B'C'} \right)\).
Do \(ABC.A'B'C'\) là lăng trụ đứng, nên ta có \(BB' \bot \left( {A'B'C'} \right)\).
Mặt khác, vectơ \(\overrightarrow {BB'} \) có giá là đường thẳng \(BB'\), do đó \(\overrightarrow {BB'} \) là một vectơ pháp tuyến của mặt phẳng \(\left( {A'B'C'} \right)\).
Trả lời câu hỏi Hoạt động 1 trang 32 SGK Toán 12 Chân trời sáng tạo
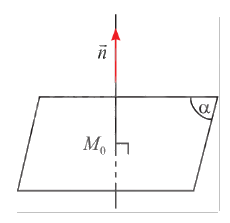
a) Cho vectơ \(\vec n\) khác \(\vec 0\). Qua một điểm \({M_0}\) cố định trong không gian, có bao nhiêu mặt phẳng \(\left( \alpha \right)\) vuông góc với giá của vectơ \(\vec n\)?
b) Cho hai vectơ \(\vec a\) và \(\vec b\) không cùng phương. Qua một điểm \({M_0}\) cố định trong không gian, có bao nhiêu mặt phẳng \(\left( \alpha \right)\) song song hoặc chứa giá của hai vectơ \(\vec a\) và \(\vec b\)?
Phương pháp giải:
Sử dụng các kiến thức về đường thẳng vuông góc mặt phẳng, đường thẳng song song với mặt phẳng đã được học ở các lớp dưới.
Lời giải chi tiết:
a) Với một điểm và một đường thẳng trong không gian, có duy nhất một mặt phẳng đi qua điểm và vuông góc với đường thẳng đó. Vậy có duy nhất một mặt phẳng \(\left( \alpha \right)\) đi qua điểm \({M_0}\) và vuông góc với giá của vectơ \(\vec n\).
b) Do hai vectơ \(\vec a\) và \(\vec b\) không cùng phương, giá của hai vectơ (lần lượt là \(a\) và \(b\)) không song song hay trùng nhau. Chọn đường thẳng \(a'\) sao cho \(a'\) song song hoặc trùng với \(a\) và \(a'\) cắt \(b\). Khi đó, có duy nhất một mặt phẳng \(\left( \beta \right)\) chứa \(a'\) và \(b\).
Nếu \({M_0} \in \left( \beta \right)\) thì mặt phẳng \(\left( \beta \right)\) là mặt phẳng duy nhất đi qua \({M_0}\) và song song hoặc chứa giá của hai vectơ \(\vec a\) và \(\vec b\).
Nếu \({M_0} \notin \left( \beta \right)\), thì trong không gian, tồn tại duy nhất mặt phẳng \(\left( \alpha \right)\) đi qua \({M_0}\) và song song với \(\left( \beta \right)\). Khi đó, \(\left( \alpha \right)\) song song hoặc chứa giá của hai vectơ \(\vec a\) và \(\vec b\).
Trả lời câu hỏi Vận dụng 1 trang 33 SGK Toán 12 Chân trời sáng tạo
Trong không gian \(Oxyz\), cho ba điểm \(A\left( {3;0;0} \right)\), \(B\left( {0;4;0} \right)\), \(C\left( {0;0;5} \right)\).
a) Tìm toạ độ của một cặp vectơ chỉ phương của mặt phẳng \(\left( {ABC} \right)\).
b) Tìm toạ độ của một vectơ pháp tuyến của mặt phẳng \(\left( {OAB} \right)\).
Phương pháp giải:
a) Chỉ ra 2 vectơ không cùng phương và có giá song song hoặc nằm trên mặt phẳng \(\left( {ABC} \right)\).
b) Chỉ ra 1 đường thẳng vuông góc với mặt phẳng \(\left( {OAB} \right)\), sau đó chọn 1 vectơ nằm trên mặt phẳng đó làm vectơ pháp tuyến của mặt phẳng \(\left( {OAB} \right)\).
Lời giải chi tiết:
a) Ta có \(\overrightarrow {AB} \left( { - 3;4;0} \right)\) và \(\overrightarrow {AC} \left( { - 3;0;5} \right)\) là hai vectơ không cùng phương và có giá nằm trong mặt phẳng \(\left( {ABC} \right)\). Vậy \(\overrightarrow {AB} \left( { - 3;4;0} \right)\) và \(\overrightarrow {AC} \left( { - 3;0;5} \right)\) là một cặp vectơ chỉ phương của mặt phẳng \(\left( {ABC} \right)\).
b) Ta thấy rằng \(A\left( {3;0;0} \right) \in Ox\), \(B\left( {0;4;0} \right) \in Oy\), \(C\left( {0;0;5} \right) \in Oz\).
Dễ dàng suy ra rằng \(OC \bot OA\) và \(OC \bot OB\), từ đó \(OC \bot \left( {OAB} \right)\).
Hơn nữa, vectơ \(\overrightarrow {OC} \left( {0;0;5} \right)\) có giá là đường thẳng \(OC\). Do đó \(\overrightarrow {OC} \left( {0;0;5} \right)\) là một vectơ pháp tuyến của mặt phẳng \(\left( {OAB} \right)\).
Trả lời câu hỏi Thực hành 1 trang 33 SGK Toán 12 Chân trời sáng tạo
Một lăng kính có dạng hình trụ đứng có đáy là tam giác đều ở hình a được vẽ lại như hình b. Tìm một cặp vectơ chỉ phương và một vectơ pháp tuyến của mặt phẳng \(\left( {A'B'C'} \right)\).
Phương pháp giải:
Để xác định một cặp vectơ chỉ phương của mặt phẳng \(\left( {A'B'C'} \right)\), chỉ ra hai vectơ không cùng phương và có giá song song hoặc nằm trong mặt phẳng \(\left( {A'B'C'} \right)\).
Để xác định một vectơ pháp tuyến của mặt phẳng \(\left( {A'B'C'} \right)\), chỉ ra một đường thẳng vuông góc với \(\left( {A'B'C'} \right)\), sau đó chọn một vectơ có giá song song hoặc trùng với đường thẳng đó.
Lời giải chi tiết:
Ta thấy rằng \(\overrightarrow {A'B'} \) và \(\overrightarrow {A'C'} \) là hai vectơ không cùng phương và có giá nằm trong mặt phẳng \(\left( {A'B'C'} \right)\). Suy ra \(\overrightarrow {A'B'} \) và \(\overrightarrow {A'C'} \) là một cặp vectơ chỉ phương của mặt phẳng \(\left( {A'B'C'} \right)\).
Do \(ABC.A'B'C'\) là lăng trụ đứng, nên ta có \(BB' \bot \left( {A'B'C'} \right)\).
Mặt khác, vectơ \(\overrightarrow {BB'} \) có giá là đường thẳng \(BB'\), do đó \(\overrightarrow {BB'} \) là một vectơ pháp tuyến của mặt phẳng \(\left( {A'B'C'} \right)\).
Mục 1 trang 32, 33 SGK Toán 12 tập 2 Chân trời sáng tạo thường xoay quanh các chủ đề về đạo hàm, ứng dụng của đạo hàm trong việc khảo sát hàm số, và các bài toán liên quan đến cực trị, giá trị lớn nhất, giá trị nhỏ nhất của hàm số. Để giải quyết hiệu quả các bài tập trong mục này, học sinh cần nắm vững các kiến thức cơ bản sau:
Để tìm đạo hàm của một hàm số, ta cần áp dụng các quy tắc tính đạo hàm đã học. Ví dụ, nếu hàm số có dạng f(x) = u(x) + v(x), thì f'(x) = u'(x) + v'(x). Tương tự, nếu hàm số có dạng f(x) = u(x) * v(x), thì f'(x) = u'(x) * v(x) + u(x) * v'(x).
Khi gặp các hàm số phức tạp, ta có thể sử dụng phương pháp biến đổi để đưa về các hàm số đơn giản hơn, sau đó áp dụng các quy tắc tính đạo hàm.
Để khảo sát hàm số bằng đạo hàm, ta thực hiện các bước sau:
Để tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng, ta thực hiện các bước sau:
Ví dụ 1: Tìm đạo hàm của hàm số f(x) = x3 + 2x2 - 5x + 1.
Giải: f'(x) = 3x2 + 4x - 5.
Ví dụ 2: Tìm cực trị của hàm số f(x) = x3 - 3x2 + 2.
Giải: f'(x) = 3x2 - 6x = 3x(x - 2). Các điểm tới hạn là x = 0 và x = 2. Lập bảng biến thiên, ta thấy hàm số đạt cực đại tại x = 0 và cực tiểu tại x = 2.
Việc giải các bài tập trong mục 1 trang 32, 33 SGK Toán 12 tập 2 Chân trời sáng tạo đòi hỏi sự nắm vững kiến thức về đạo hàm và các ứng dụng của đạo hàm. Hy vọng với hướng dẫn chi tiết và các ví dụ minh họa trên, các em học sinh sẽ tự tin hơn trong việc giải quyết các bài toán và đạt kết quả tốt trong môn Toán.