Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12 tập 1 - Chân trời sáng tạo. Bài viết này sẽ hướng dẫn bạn giải bài tập 9 trang 65 một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và đạt kết quả cao trong môn Toán.
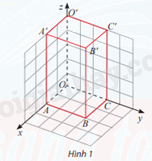
Trong không gian Oxyz, cho hình hộp chữ nhật OABC.O′A′B′C′ như Hình 1, biết B′(2; 3; 5). a) Tìm toạ độ các đỉnh còn lại của hình hộp. b) Tính độ dài đường chéo OB′ của hình hộp chữ nhật đó.
Đề bài
Trong không gian Oxyz, cho hình hộp chữ nhật OABC.O′A′B′C′ như Hình 1, biết B′(2; 3; 5).
a) Tìm toạ độ các đỉnh còn lại của hình hộp.
b) Tính độ dài đường chéo OB′ của hình hộp chữ nhật đó.
Phương pháp giải - Xem chi tiết
a) Quan sát hình vẽ, mỗi cạnh của ô vuông sẽ tương ứng với 1 đơn vị
b) Công thức tính độ lớn vecto: \(|\overrightarrow a | = \sqrt {{a_1}^2 + {a_2}^2 + {a_3}^2} \)
Lời giải chi tiết
a) O(0;0;0), A(2;0;0), B(2;3;0), C(0;3;0), O’(0;0;5), A’(2;0;5), C’(0;3;5)
b) \(\overrightarrow {OB'} = (2;3;5) \Rightarrow OB = \sqrt {{2^2} + {3^2} + {5^2}} = \sqrt {38} \)
Bài tập 9 trang 65 SGK Toán 12 tập 1 - Chân trời sáng tạo thuộc chương trình học về giới hạn của hàm số. Bài tập này yêu cầu học sinh vận dụng kiến thức về giới hạn một bên, giới hạn tại một điểm và các tính chất của giới hạn để giải quyết các bài toán cụ thể. Việc nắm vững kiến thức nền tảng và kỹ năng giải bài tập là rất quan trọng để đạt kết quả tốt trong môn Toán.
Bài tập 9 thường bao gồm các dạng bài sau:
Để giải bài tập 9 trang 65 SGK Toán 12 tập 1 - Chân trời sáng tạo một cách hiệu quả, bạn có thể áp dụng các phương pháp sau:
Ví dụ: Tính giới hạn lim (x^2 - 1)/(x - 1) khi x -> 1.
Giải:
Ta có: lim (x^2 - 1)/(x - 1) = lim (x - 1)(x + 1)/(x - 1) = lim (x + 1) = 1 + 1 = 2.
Khi giải bài tập về giới hạn, bạn cần lưu ý những điều sau:
Để củng cố kiến thức và kỹ năng giải bài tập về giới hạn, bạn có thể luyện tập thêm các bài tập sau:
Bài tập 9 trang 65 SGK Toán 12 tập 1 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh hiểu sâu hơn về khái niệm giới hạn và các ứng dụng của nó. Bằng cách nắm vững kiến thức nền tảng, áp dụng các phương pháp giải phù hợp và luyện tập thường xuyên, bạn có thể giải quyết bài tập này một cách hiệu quả và đạt kết quả tốt trong môn Toán.