Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập Toán 12 tập 1 - Chân trời sáng tạo. Bài tập 4 trang 36 là một phần quan trọng trong chương trình học, đòi hỏi học sinh nắm vững kiến thức và kỹ năng giải quyết vấn đề.
Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải chi tiết, dễ hiểu, giúp bạn hiểu rõ bản chất của bài toán và áp dụng vào các bài tập tương tự.
Khảo sát và vẽ đồ thị của các hàm số sau: a) (y = frac{{{x^2} - 2x + 2}}{{x - 1}}) b) (y = 2x - frac{1}{{1 - 2x}})
Đề bài
Khảo sát và vẽ đồ thị của các hàm số sau:
a) \(y = \frac{{{x^2} - 2x + 2}}{{x - 1}}\)
b) \(y = 2x - \frac{1}{{1 - 2x}}\)
Phương pháp giải - Xem chi tiết
Bước 1. Tìm tập xác định của hàm số
Bước 2. Xét sự biến thiên của hàm số
− Tìm đạo hàm y', xét dấu y', xác định khoảng đơn điệu của hàm số.
− Tìm giới hạn tại vô cực, giới hạn vô cực và các tiệm cận của đồ thị hàm số (nếu có)
− Lập bảng biến thiên của hàm số.
Bước 3. Vẽ đồ thị của hàm số
− Xác định các giao điểm của đồ thị với các trục toạ độ
− Vẽ các đường tiệm cận của đồ thị hàm số (nếu có).
− Vẽ đồ thị hàm số.
Lời giải chi tiết
a) \(y = \frac{{{x^2} - 2x + 2}}{{x - 1}}\)
Tập xác định: \(D = \mathbb{R}\backslash \{ 1\} \)
\(y' = \frac{{{x^2} - 2x}}{{{{(x - 1)}^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.\)
Trên các khoảng (\( - \infty \); 0), (2; \( + \infty \)) thì y' < 0 nên hàm số nghịch biến trên mỗi khoảng đó. Trên khoảng (0; 2) thì y' > 0 nên hàm số đồng biến trên khoảng đó.
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \frac{{{x^2} - 2x + 2}}{{x - 1}} = + \infty ;\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \frac{{{x^2} - 2x + 2}}{{x - 1}} = - \infty \)
\(a = \mathop {\lim }\limits_{x \to + \infty } \frac{{{x^2} - 2x + 2}}{{{x^2} - x}} = 1;b = \mathop {\lim }\limits_{x \to + \infty } (\frac{{{x^2} - 2x + 2}}{{x - 1}} - x) = - 1\) nên y = x - 1 là tiệm cận xiên của đồ thị hàm số
\(\mathop {\lim }\limits_{x \to {1^ + }} y = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{{x^2} - 2x + 2}}{{x - 1}} = + \infty ;\mathop {\lim }\limits_{x \to {1^ - }} y = \mathop {\lim }\limits_{x \to {1^ - }} \frac{{{x^2} - 2x + 2}}{{x - 1}} = - \infty \) nên x = 1 là tiệm cận đứng của đồ thị hàm số
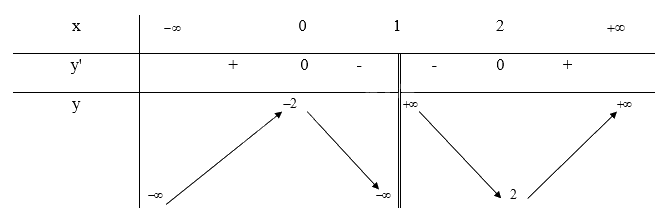
Khi x = 0 thì y = -2 nên (0;-2) là giao điểm của y với trục Oy
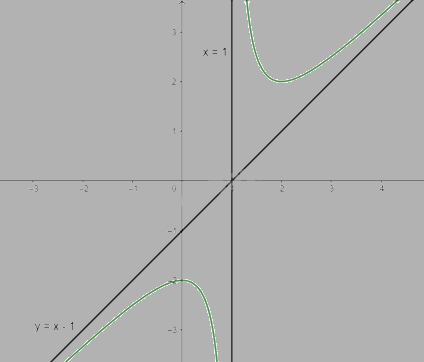
b) \(y = 2x - \frac{1}{{1 - 2x}}\)
Tập xác định: \(D = \mathbb{R}\backslash \{ \frac{1}{2}\} \)
\(y' = 2 - \frac{2}{{{{(1 - 2x)}^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1\end{array} \right.\)
Trên các khoảng (\( - \infty \); 0), (1; \( + \infty \)) thì y' > 0 nên hàm số nghịch biến trên mỗi khoảng đó. Trên khoảng (0; \(\frac{1}{2}\)) và (\(\frac{1}{2}\); 1) thì y' < 0 nên hàm số đồng biến trên khoảng đó.
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } (2x - \frac{1}{{1 - 2x}}) = + \infty ;\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } (2x - \frac{1}{{1 - 2x}}) = - \infty \)
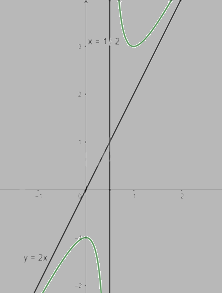
\(a = \mathop {\lim }\limits_{x \to + \infty } (2 - \frac{1}{{x - 2{x^2}}}) = 2;b = \mathop {\lim }\limits_{x \to + \infty } (2x - \frac{1}{{1 - 2x}} - 2x) = 0\) nên y = 2x là tiệm cận xiên của đồ thị hàm số
\(\mathop {\lim }\limits_{x \to {{\frac{1}{2}}^ + }} y = \mathop {\lim }\limits_{x \to {{\frac{1}{2}}^ + }} (2x - \frac{1}{{1 - 2x}}) = + \infty ;\mathop {\lim }\limits_{x \to {{\frac{1}{2}}^ - }} y = \mathop {\lim }\limits_{x \to {{\frac{1}{2}}^ - }} (2x - \frac{1}{{1 - 2x}}) = - \infty \) nên x = \(\frac{1}{2}\) là tiệm cận đứng của đồ thị hàm số
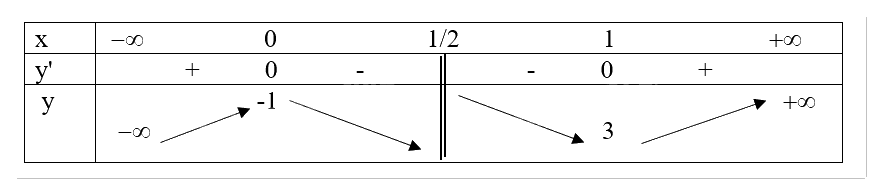
Khi x = 0 thì y = -1 nên (0;-1) là giao điểm của y với trục Oy
Bài tập 4 trang 36 SGK Toán 12 tập 1 - Chân trời sáng tạo thuộc chương trình học về giới hạn của hàm số. Để giải quyết bài tập này, học sinh cần nắm vững các khái niệm cơ bản về giới hạn, các tính chất của giới hạn và các phương pháp tính giới hạn thường gặp.
Bài tập 4 yêu cầu học sinh tính giới hạn của các hàm số khi x tiến tới một giá trị cụ thể. Các hàm số có thể là hàm đa thức, hàm hữu tỉ, hoặc các hàm số phức tạp hơn. Việc xác định đúng dạng hàm số và áp dụng phương pháp tính giới hạn phù hợp là chìa khóa để giải quyết bài tập này.
Có nhiều phương pháp để tính giới hạn của hàm số, tùy thuộc vào dạng hàm số cụ thể. Một số phương pháp thường được sử dụng bao gồm:
Dưới đây là lời giải chi tiết cho từng câu của bài tập 4 trang 36 SGK Toán 12 tập 1 - Chân trời sáng tạo:
Giới hạn của hàm số f(x) = (x^2 - 1) / (x - 1) khi x tiến tới 1.
Lời giải: Ta có thể phân tích tử số thành nhân tử: x^2 - 1 = (x - 1)(x + 1). Do đó, f(x) = (x - 1)(x + 1) / (x - 1) = x + 1 (với x ≠ 1). Vậy, lim (x→1) f(x) = lim (x→1) (x + 1) = 1 + 1 = 2.
Giới hạn của hàm số g(x) = (x^3 + 8) / (x + 2) khi x tiến tới -2.
Lời giải: Ta có thể phân tích tử số thành nhân tử: x^3 + 8 = (x + 2)(x^2 - 2x + 4). Do đó, g(x) = (x + 2)(x^2 - 2x + 4) / (x + 2) = x^2 - 2x + 4 (với x ≠ -2). Vậy, lim (x→-2) g(x) = lim (x→-2) (x^2 - 2x + 4) = (-2)^2 - 2(-2) + 4 = 4 + 4 + 4 = 12.
Khi giải bài tập về giới hạn, học sinh cần lưu ý một số điểm sau:
Kiến thức về giới hạn có ứng dụng rộng rãi trong nhiều lĩnh vực của toán học và khoa học kỹ thuật, bao gồm:
Hy vọng rằng lời giải chi tiết và hướng dẫn giải bài tập 4 trang 36 SGK Toán 12 tập 1 - Chân trời sáng tạo trên đây sẽ giúp bạn hiểu rõ hơn về kiến thức về giới hạn và áp dụng vào các bài tập tương tự. Chúc bạn học tập tốt!