Giải bài tập 1 trang 50 SGK Toán 12 tập 1 - Chân trời sáng tạo

Chào mừng các em học sinh đến với lời giải chi tiết bài tập 1 trang 50 SGK Toán 12 tập 1 - Chân trời sáng tạo. Bài viết này được giaitoan.edu.vn biên soạn nhằm hỗ trợ các em học sinh ôn tập và nắm vững kiến thức Toán 12.

Chúng tôi cung cấp lời giải đầy đủ, dễ hiểu, cùng với các phân tích chuyên sâu, giúp các em hiểu rõ bản chất của bài toán và áp dụng vào các bài tập tương tự.

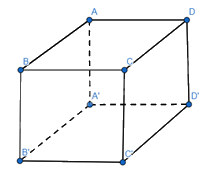
Cho hình hộp ABCD.A′B′C′D′. Chứng minh rằng: a) \(\overrightarrow {AB} + \overrightarrow {B'C'} + \overrightarrow {DD'} = \overrightarrow {AC'} \) b) \(\overrightarrow {DB'} + \overrightarrow {D'D} + \overrightarrow {BD'} = \overrightarrow {BB'} \) c) \(\overrightarrow {AC} + \overrightarrow {BA'} + \overrightarrow {DB} + \overrightarrow {C'D} = \overrightarrow 0 \)

Đề bài

Cho hình hộp ABCD.A′B′C′D′. Chứng minh rằng:

a) \(\overrightarrow {AB} + \overrightarrow {B'C'} + \overrightarrow {DD'} = \overrightarrow {AC'} \)

b) \(\overrightarrow {DB'} + \overrightarrow {D'D} + \overrightarrow {BD'} = \overrightarrow {BB'} \)

c) \(\overrightarrow {AC} + \overrightarrow {BA'} + \overrightarrow {DB} + \overrightarrow {C'D} = \overrightarrow 0 \)

Phương pháp giải - Xem chi tiết Giải bài tập 1 trang 50 SGK Toán 12 tập 1 - Chân trời sáng tạo 1

Áp dụng tính chất 2 vecto bằng nhau, quy tắc hình bình hành và quy tắc 3 điểm

Lời giải chi tiết

Giải bài tập 1 trang 50 SGK Toán 12 tập 1 - Chân trời sáng tạo 2

a) \(\overrightarrow {AB} + \overrightarrow {B'C'} + \overrightarrow {DD'} = \overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {AA'} = \overrightarrow {AC} + \overrightarrow {AA'} = \overrightarrow {AC'} \)

b) \(\overrightarrow {DB'} + \overrightarrow {D'D} + \overrightarrow {BD'} = \overrightarrow {D'B'} + \overrightarrow {BD'} = \overrightarrow {BB'} \)

c) \(\overrightarrow {AC} + \overrightarrow {BA'} + \overrightarrow {DB} + \overrightarrow {C'D} = \overrightarrow {A'C'} + \overrightarrow {DA'} + \overrightarrow {C'D} = \overrightarrow {A'D} + \overrightarrow {DA'} = \overrightarrow 0 \)

Tự tin bứt phá Kỳ thi THPT Quốc gia môn Toán! Đừng bỏ lỡ Giải bài tập 1 trang 50 SGK Toán 12 tập 1 - Chân trời sáng tạo đặc sắc thuộc chuyên mục giải sgk toán 12 trên nền tảng toán math. Với bộ bài tập toán thpt được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình Toán 12, đây chính là "chiến lược vàng" giúp các em tối ưu hóa ôn luyện. Học sinh sẽ không chỉ làm chủ mọi dạng bài thi mà còn nắm vững chiến thuật làm bài hiệu quả, sẵn sàng tự tin chinh phục điểm cao, vững bước vào đại học mơ ước nhờ phương pháp học trực quan, khoa học và hiệu quả học tập vượt trội!

Giải bài tập 1 trang 50 SGK Toán 12 tập 1 - Chân trời sáng tạo: Tổng quan

Bài tập 1 trang 50 SGK Toán 12 tập 1 - Chân trời sáng tạo thuộc chương trình học Toán 12, tập trung vào việc ôn tập các kiến thức về hàm số và đồ thị hàm số. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.

Nội dung bài tập 1 trang 50 SGK Toán 12 tập 1 - Chân trời sáng tạo

Bài tập 1 bao gồm các câu hỏi trắc nghiệm và tự luận, yêu cầu học sinh:

Xác định tập xác định của hàm số.
Tìm tập giá trị của hàm số.
Xác định tính đơn điệu của hàm số.
Vẽ đồ thị hàm số.
Giải các phương trình và bất phương trình liên quan đến hàm số.

Lời giải chi tiết bài tập 1 trang 50 SGK Toán 12 tập 1 - Chân trời sáng tạo

Câu 1: (Trắc nghiệm)

Đề bài: Hàm số y = f(x) = 2x + 1 có tập xác định là?

Lời giải: Hàm số y = f(x) = 2x + 1 là hàm số bậc nhất, xác định với mọi giá trị của x. Do đó, tập xác định của hàm số là R.

Câu 2: (Tự luận)

Đề bài: Tìm tập giá trị của hàm số y = x² - 4x + 3.

Lời giải: Hàm số y = x² - 4x + 3 là hàm số bậc hai. Để tìm tập giá trị, ta hoàn thiện bình phương:

y = x² - 4x + 4 - 1 = (x - 2)² - 1

Vì (x - 2)² ≥ 0 với mọi x, nên y ≥ -1. Vậy tập giá trị của hàm số là [-1, +∞).

Câu 3: (Trắc nghiệm)

Đề bài: Hàm số y = 1/x có tính đơn điệu trên khoảng nào?

Lời giải: Hàm số y = 1/x nghịch biến trên các khoảng (-∞, 0) và (0, +∞).

Các dạng bài tập thường gặp và phương pháp giải

Trong quá trình giải các bài tập về hàm số và đồ thị hàm số, học sinh thường gặp các dạng bài sau:

Xác định tập xác định: Cần chú ý đến các điều kiện để hàm số có nghĩa, ví dụ: mẫu số khác 0, căn thức không âm, logarit có cơ số lớn hơn 0 và khác 1.
Tìm tập giá trị: Sử dụng các phương pháp như hoàn thiện bình phương, tìm giá trị lớn nhất và nhỏ nhất của hàm số, hoặc xét giới hạn của hàm số khi x tiến tới vô cùng.
Xác định tính đơn điệu: Sử dụng đạo hàm của hàm số để xét dấu và kết luận về tính đơn điệu.
Vẽ đồ thị hàm số: Xác định các điểm đặc biệt của đồ thị như điểm cắt trục, điểm cực trị, điểm uốn, và vẽ đồ thị dựa trên các thông tin đó.

Mẹo học tập hiệu quả

Để học tốt môn Toán 12, đặc biệt là các bài tập về hàm số và đồ thị hàm số, học sinh cần:

Nắm vững các kiến thức cơ bản về hàm số, đạo hàm, và tích phân.
Luyện tập thường xuyên các bài tập từ dễ đến khó.
Sử dụng các công cụ hỗ trợ học tập như máy tính bỏ túi, phần mềm vẽ đồ thị.
Tìm kiếm sự giúp đỡ từ giáo viên và bạn bè khi gặp khó khăn.

Kết luận

Bài tập 1 trang 50 SGK Toán 12 tập 1 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số và đồ thị hàm số. Hy vọng với lời giải chi tiết và các hướng dẫn trên, các em học sinh sẽ tự tin hơn trong việc giải quyết các bài tập tương tự.