Giải bài tập 7 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo

Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12 tập 1 - Chân trời sáng tạo. Bài viết này sẽ giúp bạn nắm vững kiến thức và kỹ năng giải toán một cách hiệu quả.

Chúng tôi hiểu rằng việc tự học Toán đôi khi gặp nhiều khó khăn. Vì vậy, đội ngũ giaitoan.edu.vn đã biên soạn lời giải bài tập 7 trang 18 SGK Toán 12 tập 1 một cách cẩn thận, đảm bảo tính chính xác và dễ tiếp thu.

Hộp sữa \(1l\) được thiết kế dạng hình hộp chữ nhật với đáy là hình vuông cạnh x cm. Tìm x để diện tích toàn phần của hộp nhỏ nhất.

Đề bài

Hộp sữa \(1l\) được thiết kế dạng hình hộp chữ nhật với đáy là hình vuông cạnh x cm. Tìm x để diện tích toàn phần của hộp nhỏ nhất.

Phương pháp giải - Xem chi tiết Giải bài tập 7 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo 1

Tìm mối liên hệ giữa chiều cao và cạnh đáy, từ đó lập hàm số biểu diễn diện tích toàn phần của hộp theo x. Sau đó tìm đạo hàm, lập bảng biến thiên và xác định giá trị nhỏ nhất

Lời giải chi tiết

Gọi chiều cao của hộp là h (cm)

Thể tích của hộp là: \(V = h.{x^2} = 1 \Leftrightarrow h = \frac{1}{{{x^2}}}\)

Diện tích toàn phần của hộp là: \(y = {S_{tp}} = {S_{xq}} + {S_{day}} = 4hx + 2{x^2} = 4.\frac{1}{{{x^2}}}.x + 2{x^2} = 2{x^2} + \frac{4}{x}\)

Tập xác định: \(D = (0; + \infty )\)

\(y' = 4x - \frac{4}{{{x^2}}} = 0 \Leftrightarrow x = 1\)

Bảng biến thiên:

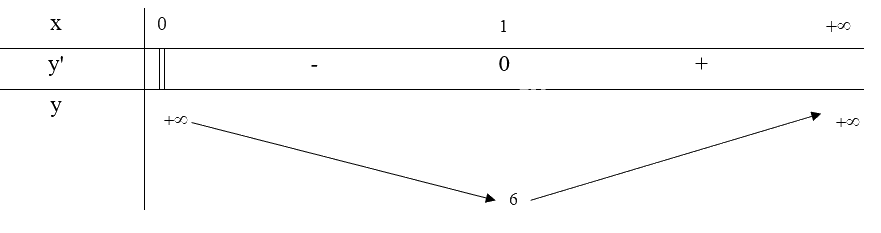
Giải bài tập 7 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo 2

Từ bảng biến thiên, ta thấy \(\mathop {\min }\limits_D y = y(1) = 6\)

Vậy x = 1cm thì diện tích toàn phần của hộp nhỏ nhất và bằng 6 \(c{m^2}\)

Tự tin bứt phá Kỳ thi THPT Quốc gia môn Toán! Đừng bỏ lỡ Giải bài tập 7 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo đặc sắc thuộc chuyên mục toán 12 trên nền tảng tài liệu toán. Với bộ bài tập lý thuyết toán thpt được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình Toán 12, đây chính là "chiến lược vàng" giúp các em tối ưu hóa ôn luyện. Học sinh sẽ không chỉ làm chủ mọi dạng bài thi mà còn nắm vững chiến thuật làm bài hiệu quả, sẵn sàng tự tin chinh phục điểm cao, vững bước vào đại học mơ ước nhờ phương pháp học trực quan, khoa học và hiệu quả học tập vượt trội!

Giải bài tập 7 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo: Tổng quan và Phương pháp giải

Bài tập 7 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo thuộc chương trình học về giới hạn của hàm số. Đây là một phần kiến thức nền tảng quan trọng trong chương trình Toán 12, giúp học sinh hiểu rõ hơn về khái niệm giới hạn và ứng dụng của nó trong việc giải các bài toán thực tế.

Nội dung bài tập 7 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo

Bài tập 7 yêu cầu học sinh tính giới hạn của hàm số tại một điểm cho trước. Để giải bài tập này, học sinh cần nắm vững các định nghĩa và tính chất của giới hạn, cũng như các phương pháp tính giới hạn thường gặp như phương pháp chia, phương pháp nhân liên hợp, và phương pháp sử dụng định lý giới hạn.

Phương pháp giải bài tập 7 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo

Xác định dạng của hàm số: Xác định xem hàm số là hàm đa thức, hàm hữu tỉ, hay hàm khác.
Áp dụng định nghĩa giới hạn: Nếu hàm số liên tục tại điểm cần tính giới hạn, ta có thể thay trực tiếp giá trị của điểm đó vào hàm số để tính giới hạn.
Sử dụng các tính chất của giới hạn: Áp dụng các tính chất của giới hạn như giới hạn của tổng, hiệu, tích, thương, và lũy thừa.
Sử dụng các phương pháp tính giới hạn: Nếu hàm số không liên tục tại điểm cần tính giới hạn, ta cần sử dụng các phương pháp tính giới hạn như phương pháp chia, phương pháp nhân liên hợp, và phương pháp sử dụng định lý giới hạn.

Lời giải chi tiết bài tập 7 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo

Bài tập: Tính các giới hạn sau: a) lim_x→2 (x² + 3x - 1) b) lim_x→-1 (2x³ - 5x + 3) c) lim_x→0 (x² + 1) / (x - 2)

Lời giải:

a) lim_x→2 (x² + 3x - 1)Vì hàm số f(x) = x² + 3x - 1 là hàm đa thức, nên nó liên tục tại x = 2. Do đó, ta có thể thay trực tiếp x = 2 vào hàm số để tính giới hạn:lim_x→2 (x² + 3x - 1) = 2² + 3*2 - 1 = 4 + 6 - 1 = 9
b) lim_x→-1 (2x³ - 5x + 3)Tương tự như câu a, hàm số f(x) = 2x³ - 5x + 3 là hàm đa thức, nên nó liên tục tại x = -1. Do đó:lim_x→-1 (2x³ - 5x + 3) = 2*(-1)³ - 5*(-1) + 3 = -2 + 5 + 3 = 6
c) lim_x→0 (x² + 1) / (x - 2)Hàm số f(x) = (x² + 1) / (x - 2) là hàm hữu tỉ, và nó liên tục tại x = 0. Do đó:lim_x→0 (x² + 1) / (x - 2) = (0² + 1) / (0 - 2) = 1 / -2 = -1/2

Ví dụ minh họa và bài tập tương tự

Để hiểu rõ hơn về cách tính giới hạn, chúng ta hãy xem xét một số ví dụ minh họa và bài tập tương tự:

Ví dụ 1: Tính lim_x→1 (x³ - 1) / (x - 1)
Bài tập 1: Tính lim_x→3 (x² - 9) / (x - 3)
Bài tập 2: Tính lim_x→-2 (x² + 4x + 4) / (x + 2)

Lưu ý quan trọng khi giải bài tập về giới hạn

Khi giải bài tập về giới hạn, cần lưu ý một số điểm sau:

Kiểm tra xem hàm số có liên tục tại điểm cần tính giới hạn hay không.
Nếu hàm số không liên tục, cần sử dụng các phương pháp tính giới hạn phù hợp.
Chú ý đến các dạng giới hạn đặc biệt như giới hạn vô cùng.

Kết luận

Bài tập 7 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về giới hạn của hàm số. Hy vọng rằng với lời giải chi tiết và phương pháp giải được trình bày trong bài viết này, các bạn học sinh sẽ tự tin hơn khi giải các bài tập tương tự.