Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập Toán 12 tập 2 theo chương trình Chân trời sáng tạo. Bài viết này sẽ giúp bạn hiểu rõ cách giải bài tập 7 trang 81, từ đó nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng trình bày lời giải một cách dễ hiểu, logic, kèm theo các ví dụ minh họa cụ thể để bạn có thể áp dụng vào các bài tập tương tự.
Có hai cái hộp giống nhau, hộp thứ nhất chứa 5 quả bóng bàn màu trắng và 3 quả bóng bàn màu vàng, hộp thứ hai chứa 4 quả bóng bàn màu trắng và 6 quả bóng bàn màu vàng. Các quả bóng có cùng kích thước và khối lượng. Minh lấy ra ngẫu nhiên 1 quả bóng từ hộp thứ nhất. Nếu quả bóng đó là bóng vàng thì Minh lấy ra ngẫu nhiên đồng thời 2 quả bóng từ hộp thứ hai; nếu quả bóng đó màu trắng thì Minh lấy ra ngẫu nhiên 3 quả bóng từ hộp thứ hai. a) Sử dụng sơ đồ hình cây, tính xác suất để có đúng 1 quả bó
Đề bài
Có hai cái hộp giống nhau, hộp thứ nhất chứa 5 quả bóng bàn màu trắng và 3 quả bóng bàn màu vàng, hộp thứ hai chứa 4 quả bóng bàn màu trắng và 6 quả bóng bàn màu vàng. Các quả bóng có cùng kích thước và khối lượng. Minh lấy ra ngẫu nhiên 1 quả bóng từ hộp thứ nhất. Nếu quả bóng đó là bóng vàng thì Minh lấy ra ngẫu nhiên đồng thời 2 quả bóng từ hộp thứ hai; nếu quả bóng đó màu trắng thì Minh lấy ra ngẫu nhiên 3 quả bóng từ hộp thứ hai.
a) Sử dụng sơ đồ hình cây, tính xác suất để có đúng 1 quả bóng màu vàng trong các quả bóng lấy ra từ hộp thứ hai.
b) Biết rằng các quả bóng lấy ra từ hộp thứ hai đều có màu trắng. Tính xác suất để quả bóng lấy ra từ hộp thứ nhất có màu vàng.
Phương pháp giải - Xem chi tiết
a) Gọi \(A\) là biến cố “Lấy được quả bóng vàng ở hộp thứ nhất”, \(B\) là biến cố “Chọn được đúng 1 quả bóng vàng ở hộp thứ hai”.
Sử dụng sơ đồ hình cây và công thức tính xác suất toàn phần để tính \(P\left( B \right)\).
b) Gọi \(C\) là biến cố “Tất cả quả bóng lấy ra ở hộp thứ hai đều có màu trắng”. Xác suất cần tính là \(P\left( {A|C} \right)\). Sử dụng công thức Bayes để tính xác suất này.
Lời giải chi tiết
Gọi \(A\) là biến cố “Lấy được quả bóng vàng ở hộp thứ nhất”, \(B\) là biến cố “Chọn được đúng 1 quả bóng vàng ở hộp thứ hai”.
Ta có \(P\left( A \right) = \frac{3}{{3 + 5}} = \frac{3}{8}\) và \(P\left( {\bar A} \right) = 1 - \frac{3}{8} = \frac{5}{8}\).
Khi lấy được quả bóng vàng ở hộp thứ nhất, Minh sẽ lấy ngẫu nhiên đồng thời 2 quả bóng ở hộp thứ hai. Do đó \(P\left( {B|A} \right) = \frac{{4.6}}{{C_{10}^2}} = \frac{8}{{15}}\).
Khi lấy được quả bóng trắng ở hộp thứ nhất, Minh sẽ lấy ngẫu nhiên đồng thời 3 quả bóng ở hộp thứ hai. Do đó \(P\left( {B|\bar A} \right) = \frac{{6.C_4^2}}{{C_{10}^3}} = \frac{3}{{10}}\).
Vậy ta có sơ đồ hình cây sau:
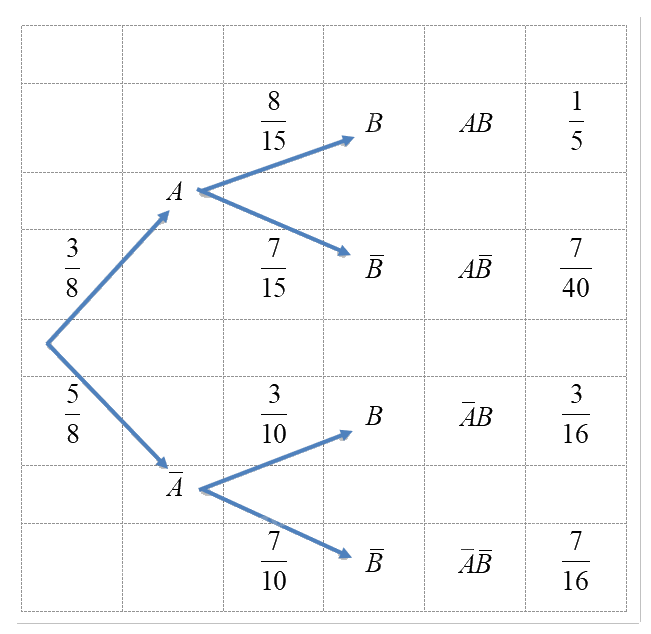Dựa vào sơ đồ hình cây, ta có \(P\left( B \right) = \frac{1}{5} + \frac{3}{{16}} = \frac{{31}}{{80}}\).
b) Gọi \(C\) là biến cố “Tất cả quả bóng lấy ra ở hộp thứ hai đều có màu trắng”. Xác suất cần tính là \(P\left( {A|C} \right)\).
Ta có \(P\left( C \right) = P\left( A \right).P\left( {C|A} \right) + P\left( {\bar A} \right).P\left( {C|\bar A} \right)\).
Nếu lấy được quả bóng màu vàng ở hộp thứ nhất, Minh sẽ lấy đồng thời ngẫu nhiên 2 quả ở hộp thứ hai. Do đó \(P\left( {C|A} \right) = \frac{{C_4^2}}{{C_{10}^2}} = \frac{2}{{15}}\).
Nếu lấy được quả bóng màu trắng ở hộp thứ nhất, Minh sẽ lấy đồng thời ngẫu nhiên 3 quả ở hộp thứ hai. Do đó \(P\left( {C|\bar A} \right) = \frac{{C_4^3}}{{C_{10}^3}} = \frac{1}{{30}}\).
Như vậy \(P\left( C \right) = \frac{3}{8}.\frac{2}{{15}} + \frac{5}{8}.\frac{1}{{30}} = \frac{{17}}{{240}}\).
Vậy theo công thức Bayes, xác suất để xác suất để quả bóng lấy ra từ hộp thứ nhất có màu vàng là \(P\left( {A|C} \right) = \frac{{P\left( A \right).P\left( {C|A} \right)}}{{P\left( C \right)}} = \frac{{\frac{3}{8}.\frac{2}{{15}}}}{{\frac{{17}}{{240}}}} = \frac{{12}}{{17}}\).
Bài tập 7 trang 81 SGK Toán 12 tập 2 thuộc chương trình Chân trời sáng tạo tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế liên quan đến tốc độ thay đổi của một đại lượng. Bài tập này thường yêu cầu học sinh phải hiểu rõ các khái niệm như đạo hàm, quy tắc tính đạo hàm, và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.
Bài tập 7 thường có dạng như sau: Một vật thể chuyển động theo một quỹ đạo được mô tả bởi một hàm số. Yêu cầu là tìm vận tốc và gia tốc của vật thể tại một thời điểm nhất định, hoặc xác định thời điểm vật thể đạt vận tốc cực đại hoặc cực tiểu.
Ví dụ: Một vật thể chuyển động theo hàm vị trí s(t) = t3 - 6t2 + 9t + 2 (trong đó s tính bằng mét và t tính bằng giây). Tìm vận tốc và gia tốc của vật thể tại thời điểm t = 2 giây.
Giải:
Để củng cố kiến thức và kỹ năng giải bài tập về đạo hàm và ứng dụng của đạo hàm, bạn có thể tham khảo thêm các bài tập tương tự trong SGK Toán 12 tập 2 Chân trời sáng tạo, hoặc tìm kiếm trên các trang web học toán online uy tín. Việc luyện tập thường xuyên sẽ giúp bạn tự tin hơn khi đối mặt với các bài toán khó.
Bài tập 7 trang 81 SGK Toán 12 tập 2 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh hiểu rõ hơn về ứng dụng của đạo hàm trong việc giải quyết các bài toán thực tế. Hy vọng với hướng dẫn chi tiết và ví dụ minh họa trên, bạn đã có thể tự tin giải quyết bài tập này và đạt kết quả tốt trong môn Toán.
