Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập Toán 12 tập 2. Bài viết này sẽ hướng dẫn bạn giải bài tập 5 trang 20 SGK Toán 12 tập 2 theo chương trình Chân trời sáng tạo.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi luôn cố gắng trình bày lời giải một cách dễ hiểu nhất, giúp bạn nắm vững kiến thức và tự tin hơn trong học tập.
Mặt cắt ngang của một ống dẫn khí nóng là một hình vành khuyên như hình dưới đây. Khí bên trong ống được duy trì ở \({150^o}{\rm{C}}\). Biết rằng nhiệt độ \(T\left( {^oC} \right)\) tại điểm A trên thành ống là hàm số của khoảng cách \(x{\rm{ }}\left( {{\rm{cm}}} \right)\) từ A đến tâm của mặt cắt và \(T'\left( x \right) = - \frac{{30}}{x}\) \(\left( {6 \le x \le 8} \right)\). Tìm nhiệt độ mặt ngoài của ống.
Đề bài
Mặt cắt ngang của một ống dẫn khí nóng là một hình vành khuyên như hình dưới đây. Khí bên trong ống được duy trì ở \({150^o}{\rm{C}}\). Biết rằng nhiệt độ \(T\left( {^oC} \right)\) tại điểm A trên thành ống là hàm số của khoảng cách \(x{\rm{ }}\left( {{\rm{cm}}} \right)\) từ A đến tâm của mặt cắt và \(T'\left( x \right) = - \frac{{30}}{x}\) \(\left( {6 \le x \le 8} \right)\). Tìm nhiệt độ mặt ngoài của ống.
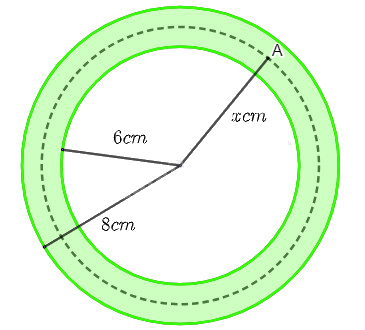
Phương pháp giải - Xem chi tiết
Do nhiệt độ của khí bên trong ống luôn được duy trì ở \({150^o}{\rm{C}}\), nên \(T\left( 6 \right) = 150\).
Nhiệt độ mặt ngoài của ống là \(T\left( 8 \right) = \left[ {T\left( 8 \right) - T\left( 6 \right)} \right] + T\left( 6 \right) = \int\limits_6^8 {T'\left( x \right)dx} + T\left( 6 \right)\).
Lời giải chi tiết
Do nhiệt độ của khí bên trong ống luôn được duy trì ở \({150^o}{\rm{C}}\), nên \(T\left( 6 \right) = 150\).
Nhiệt độ mặt ngoài của ống là \(T\left( 8 \right) = \left[ {T\left( 8 \right) - T\left( 6 \right)} \right] + T\left( 6 \right) = \int\limits_6^8 {T'\left( x \right)dx} + T\left( 6 \right)\).
Ta có \(\int\limits_6^8 {T'\left( x \right)dx} = \int\limits_6^8 { - \frac{{30}}{x}dx} = - 30\int\limits_6^8 {\frac{1}{x}dx = - 30.\left. {\left( {\ln \left| x \right|} \right)} \right|_6^8 = - 30\ln 8 + 30\ln 6} \).
Vậy nhiệt độ bên ngoài mặt ống là \(T\left( 8 \right) = - 30\ln 8 + 30\ln 6 + 150 \approx 141,{37^o}C\)
Bài tập 5 trang 20 SGK Toán 12 tập 2 chương trình Chân trời sáng tạo thuộc chủ đề về đạo hàm của hàm số. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế, cụ thể là tìm đạo hàm của hàm số và phân tích các tính chất của đạo hàm.
Bài tập 5 bao gồm các câu hỏi nhỏ, yêu cầu học sinh:
Cho hàm số f(x) = x3 - 3x2 + 2. Tính f'(x).
Lời giải:
Áp dụng quy tắc đạo hàm của tổng và lũy thừa, ta có:
f'(x) = 3x2 - 6x
Cho hàm số g(x) = sin(2x). Tính g'(x).
Lời giải:
Áp dụng quy tắc đạo hàm của hàm hợp, ta có:
g'(x) = 2cos(2x)
Cho hàm số h(x) = ex + ln(x). Tính h'(x).
Lời giải:
Áp dụng quy tắc đạo hàm của hàm mũ và logarit, ta có:
h'(x) = ex + 1/x
Đạo hàm đóng vai trò quan trọng trong việc giải bài tập 5 trang 20 SGK Toán 12 tập 2. Cụ thể:
Để giải bài tập về đạo hàm hiệu quả, bạn có thể áp dụng một số mẹo sau:
Để củng cố kiến thức về đạo hàm, bạn có thể làm thêm các bài tập tương tự sau:
Bài tập 5 trang 20 SGK Toán 12 tập 2 chương trình Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng vận dụng kiến thức về đạo hàm. Hy vọng với lời giải chi tiết và các mẹo giải bài tập trên, bạn sẽ tự tin hơn trong việc giải quyết các bài toán tương tự.