Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập Toán 12 tập 1 - Chân trời sáng tạo. Bài tập 5 trang 36 thuộc chương trình học quan trọng, đòi hỏi sự hiểu biết sâu sắc về kiến thức đã học.
Chúng tôi cam kết mang đến cho bạn trải nghiệm học toán online tốt nhất, giúp bạn nắm vững kiến thức và tự tin giải quyết các bài toán khó.
Cho hàm số: (y = frac{{ - {x^2} + 3x + 1}}{{x + 2}}) a) Khảo sát và vẽ đồ thị của hàm số đã cho. b) Tìm toạ độ trung điểm đoạn nối hai điểm cực trị của đồ thị hàm số. Có nhận xét gì về điểm này?
Đề bài
Cho hàm số: \(y = \frac{{ - {x^2} + 3x + 1}}{{x + 2}}\)
a) Khảo sát và vẽ đồ thị của hàm số đã cho.
b) Tìm toạ độ trung điểm đoạn nối hai điểm cực trị của đồ thị hàm số. Có nhận xét gì về điểm này?
Phương pháp giải - Xem chi tiết
a) Bước 1. Tìm tập xác định của hàm số
Bước 2. Xét sự biến thiên của hàm số
− Tìm đạo hàm y', xét dấu y', xác định khoảng đơn điệu của hàm số.
− Tìm giới hạn tại vô cực, giới hạn vô cực và các tiệm cận của đồ thị hàm số (nếu có)
− Lập bảng biến thiên của hàm số.
Bước 3. Vẽ đồ thị của hàm số
− Xác định các giao điểm của đồ thị với các trục toạ độ
− Vẽ các đường tiệm cận của đồ thị hàm số (nếu có).
− Vẽ đồ thị hàm số.
b) Tọa độ của trung điểm của đoạn thẳng nối 2 điểm có hoành độ bằng trung bình cộng hoành độ 2 điểm, tung độ bằng trung bình cộng trung bình 2 điểm
Lời giải chi tiết
a) Tập xác định: \(D = \mathbb{R}\backslash \{ - 2\} \)
\(y' = \frac{{ - {x^2} - 4x + 5}}{{{{(x + 2)}^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 5\\x = 1\end{array} \right.\)
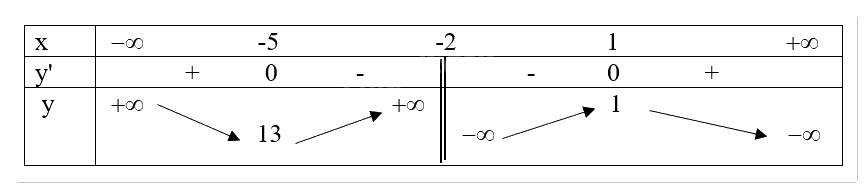
Trên các khoảng (\( - \infty \); -5), (1; \( + \infty \)) thì y' > 0 nên hàm số nghịch biến trên mỗi khoảng đó. Trên khoảng (-5; -2) và (-2;1) thì y' < 0 nên hàm số đồng biến trên khoảng đó.
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - {x^2} + 3x + 1}}{{x + 2}} = - \infty ;\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \frac{{ - {x^2} + 3x + 1}}{{x + 2}} = + \infty \)
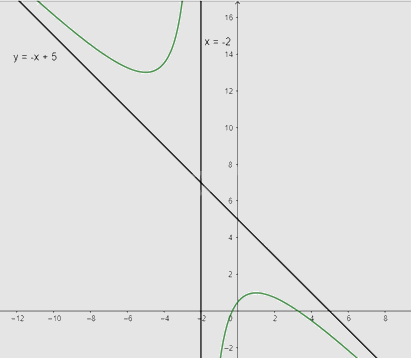
\(a = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - {x^2} + 3x + 1}}{{{x^2} + 2x}} = - 1;b = \mathop {\lim }\limits_{x \to + \infty } (\frac{{{x^2} - 2x + 2}}{{x - 1}} + x) = 5\) nên y = -x + 5 là tiệm cận xiên của đồ thị hàm số
\(\mathop {\lim }\limits_{x \to - {2^ + }} y = \mathop {\lim }\limits_{x \to - {2^ + }} \frac{{ - {x^2} + 3x + 1}}{{x + 2}} = - \infty ;\mathop {\lim }\limits_{x \to - {2^ - }} y = \mathop {\lim }\limits_{x \to - {2^ - }} \frac{{{x^2} - 2x + 2}}{{x - 1}} = + \infty \) nên x = -2 là tiệm cận đứng của đồ thị hàm số
Khi x = 0 thì y = \(\frac{1}{2}\) nên (0; \(\frac{1}{2}\)) là giao điểm của y với trục Oy
b) Hàm số đạt cực tiểu tại x = -5 và \({y_{ct}} = 13\)
Hàm số đạt cực đại tại x = 1 và \({y_{cd}} = 1\)
Trung điểm đoạn nối hai điểm cực trị của đồ thị hàm số có tọa độ là \((\frac{{ - 5 + 1}}{2};\frac{{13 + 1}}{2}) = ( - 2;7)\). Điểm này là giao điểm của tiệm cận đứng và tiệm cận xiên của đồ thị hàm số
Bài tập 5 trang 36 SGK Toán 12 tập 1 - Chân trời sáng tạo là một phần quan trọng trong chương trình học về giới hạn của hàm số. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về giới hạn, các định lý liên quan và các phương pháp tính giới hạn thường gặp.
Bài tập 5 thường xoay quanh việc tính giới hạn của hàm số tại một điểm, sử dụng các định lý về giới hạn của tổng, hiệu, tích, thương và hàm hợp. Đôi khi, bài tập có thể yêu cầu học sinh chứng minh sự tồn tại của giới hạn hoặc tìm giới hạn của hàm số khi x tiến tới vô cùng.
Để giải bài tập 5 trang 36 SGK Toán 12 tập 1 - Chân trời sáng tạo, học sinh có thể áp dụng các phương pháp sau:
Ví dụ: Tính giới hạn lim (x^2 - 1) / (x - 1) khi x -> 1.
Giải:
Ta có thể phân tích tử thức thành (x - 1)(x + 1). Do đó:
lim (x^2 - 1) / (x - 1) = lim (x - 1)(x + 1) / (x - 1) = lim (x + 1) = 1 + 1 = 2.
Để nắm vững kiến thức và kỹ năng giải bài tập 5 trang 36 SGK Toán 12 tập 1 - Chân trời sáng tạo, học sinh nên:
Ngoài bài tập 5 trang 36, học sinh cũng nên luyện tập các bài tập khác trong SGK Toán 12 tập 1 - Chân trời sáng tạo để hiểu sâu hơn về chương trình học. Các bài tập liên quan bao gồm:
Giải bài tập 5 trang 36 SGK Toán 12 tập 1 - Chân trời sáng tạo đòi hỏi sự nắm vững kiến thức cơ bản và kỹ năng giải bài tập. Bằng cách áp dụng các phương pháp giải phù hợp và luyện tập thường xuyên, học sinh có thể tự tin giải quyết bài tập này và đạt kết quả tốt trong môn Toán.