Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 12 và 13 sách giáo khoa Toán 12 tập 2, chương trình Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong môn học Toán.
Diện tích hình thang cong
Trả lời câu hỏi Thực hành 1 trang 13 SGK Toán 12 Chân trời sáng tạo
Tính diện tích hình thang cong giới hạn bởi đồ thị hàm số \(y = f\left( x \right) = {e^x}\), trục hoành, trục tung và đường thẳng \(x = 1\).
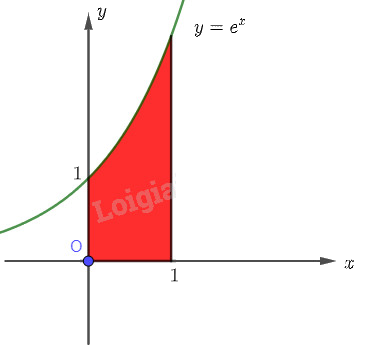
Phương pháp giải:
Tìm một nguyên hàm \(F\left( x \right)\) của hàm số \(f\left( x \right)\), sau đó sử dụng công thức để tính diện tích hình thang cong \(S = F\left( b \right) - F\left( a \right)\).
Lời giải chi tiết:
Ta có hàm số \(y = f\left( x \right) = {e^x}\) liên tục và dương trên đoạn \(\left[ {0;1} \right]\).
Ta có \(\int {f\left( x \right)dx} = \int {{e^x}dx} = {e^x} + C\), từ đó suy ra \(F\left( x \right) = {e^x}\) là một nguyên hàm của \(f\left( x \right) = {e^x}\).
Diện tích hình thang cong cần tính là: \(S = F\left( 1 \right) - F\left( 0 \right) = {e^1} - {e^0} = e - 1\).
Trả lời câu hỏi Khám phá 1 trang 12 SGK Toán 12 Chân trời sáng tạo
Cho hàm số \(y = f\left( x \right) = x + 1\). Với mỗi \(x \ge 1\), kí hiệu \(S\left( x \right)\) là diện tích của hình thang giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành và hai đường thẳng vuông góc với \(Ox\) tại các điểm có hoành độ 1 và \(x\).
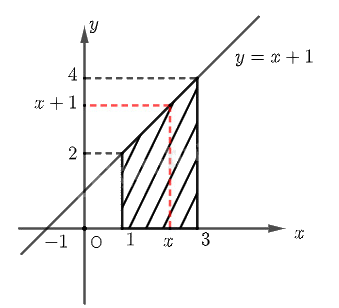
a) Tính \(S\left( 3 \right)\).
b) Tính \(S\left( x \right)\) với mỗi \(x \ge 1\).
c) Tính \(S'\left( x \right)\). Từ đó suy ra \(S\left( x \right)\) là một nguyên hàm của \(f\left( x \right)\) trên \(\left[ {1; + \infty } \right)\).
d) Cho \(F\left( x \right)\) là một nguyên hàm của hàm số \(f\left( x \right)\). Chứng tỏ rằng \(F\left( 3 \right) - F\left( 1 \right) = S\left( 3 \right)\). Từ đó nhận xét về cách tính \(S\left( 3 \right)\) khi biết một nguyên hàm của \(f\left( x \right)\).
Phương pháp giải:
a, b) Gọi các điểm \(A\), \(B\), \(C\), \(D\) là các đỉnh của hình thang như hình vẽ. Tính độ dài các cạnh \(AD\), \(BC\) và \(AB\), rồi sử dụng công thức tính diện tích hình thang \({S_{ABCD}} = \frac{{\left( {AD + BC} \right).AB}}{2}\) để tính \(S\left( 3 \right)\) ở câu a và \(S\left( x \right)\) ở câu b.
c) Sử dụng công thức đạo hàm để tính \(S'\left( x \right)\) và kết luận.
d) Tính nguyên hàm của \(f\left( x \right)\), sau đó tính \(F\left( 3 \right) - F\left( 1 \right)\), so sánh với \(S\left( 3 \right)\)
Lời giải chi tiết:
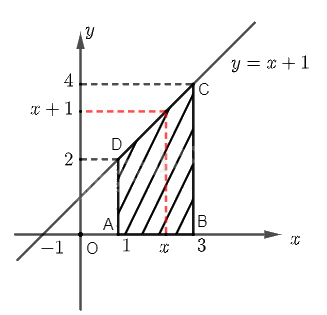
a) Gọi các điểm \(A\), \(B\), \(C\), \(D\) là các đỉnh của hình thang như hình vẽ. Dễ thấy rằng \(ABCD\) là hình thang vuông có hai đáy là \(AD\) và \(BC\), chiều cao là \(AB\).
Ta có \(AB = 3 - 1 = 2\), \(AD = 2\) và \(BC = 4\). Do đó diện tích hình thang \(ABCD\) là:
\(S\left( 3 \right) = \frac{{\left( {2 + 4} \right).2}}{2} = 6\).
b) Tương tự câu a, nhưng hoành độ của \(B\) là \(x\), ta suy ra tung độ của \(C\) là \(x + 1\).
Ta có \(AB = x - 1\), \(AD = 2\), \(BC = x + 1\). Do đó diện tích hình thang \(ABCD\) là:
\(S\left( x \right) = \frac{{\left( {AD + BC} \right).AB}}{2} = \frac{{\left( {2 + x + 1} \right)\left( {x - 1} \right)}}{2} = \frac{{\left( {x + 3} \right)\left( {x - 1} \right)}}{2} = \frac{{{x^2} + 2x - 3}}{2}\)
c) Ta có \(S'\left( x \right) = \frac{{2x + 2}}{2} = x + 1 = f\left( x \right)\). Vậy \(S\left( x \right)\) là một nguyên hàm của \(f\left( x \right)\).
d) Do \(F\left( x \right)\) là một nguyên hàm của \(f\left( x \right)\), ta có:
\(F\left( x \right) = \int {f\left( x \right)dx} = \int {\left( {x + 1} \right)dx} = \frac{{{x^2}}}{2} + x + C\)
Suy ra \(F\left( 3 \right) = \frac{{{3^2}}}{2} + 3 + C = \frac{{15}}{2} + C\) và \(F\left( 1 \right) = \frac{{{1^2}}}{2} + 1 + C = \frac{3}{2} + C\)
Như vậy ta có \(F\left( 3 \right) - F\left( 1 \right) = \left( {\frac{{15}}{2} + C} \right) - \left( {\frac{3}{2} + C} \right) = 6 = S\left( 3 \right)\).
Do đó, để tính \(S\left( 3 \right)\) khi biết một nguyên hàm của \(f\left( x \right)\), ta thực hiện tính nguyên hàm \(F\left( x \right)\) của \(f\left( x \right)\), sau đó ta tính \(F\left( 3 \right)\) và \(F\left( 1 \right)\), từ đó tính được \(S\left( 3 \right) = F\left( 3 \right) - F\left( 1 \right)\).
Trả lời câu hỏi Khám phá 1 trang 12 SGK Toán 12 Chân trời sáng tạo
Cho hàm số \(y = f\left( x \right) = x + 1\). Với mỗi \(x \ge 1\), kí hiệu \(S\left( x \right)\) là diện tích của hình thang giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành và hai đường thẳng vuông góc với \(Ox\) tại các điểm có hoành độ 1 và \(x\).
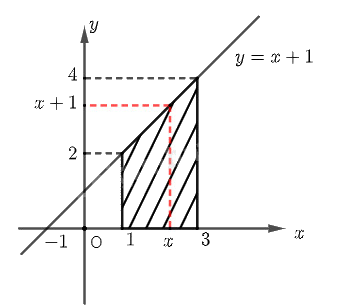
a) Tính \(S\left( 3 \right)\).
b) Tính \(S\left( x \right)\) với mỗi \(x \ge 1\).
c) Tính \(S'\left( x \right)\). Từ đó suy ra \(S\left( x \right)\) là một nguyên hàm của \(f\left( x \right)\) trên \(\left[ {1; + \infty } \right)\).
d) Cho \(F\left( x \right)\) là một nguyên hàm của hàm số \(f\left( x \right)\). Chứng tỏ rằng \(F\left( 3 \right) - F\left( 1 \right) = S\left( 3 \right)\). Từ đó nhận xét về cách tính \(S\left( 3 \right)\) khi biết một nguyên hàm của \(f\left( x \right)\).
Phương pháp giải:
a, b) Gọi các điểm \(A\), \(B\), \(C\), \(D\) là các đỉnh của hình thang như hình vẽ. Tính độ dài các cạnh \(AD\), \(BC\) và \(AB\), rồi sử dụng công thức tính diện tích hình thang \({S_{ABCD}} = \frac{{\left( {AD + BC} \right).AB}}{2}\) để tính \(S\left( 3 \right)\) ở câu a và \(S\left( x \right)\) ở câu b.
c) Sử dụng công thức đạo hàm để tính \(S'\left( x \right)\) và kết luận.
d) Tính nguyên hàm của \(f\left( x \right)\), sau đó tính \(F\left( 3 \right) - F\left( 1 \right)\), so sánh với \(S\left( 3 \right)\)
Lời giải chi tiết:
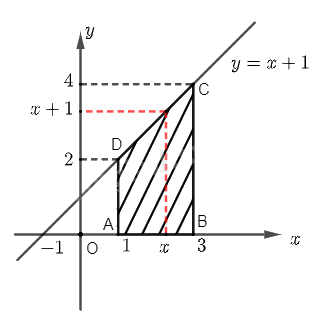
a) Gọi các điểm \(A\), \(B\), \(C\), \(D\) là các đỉnh của hình thang như hình vẽ. Dễ thấy rằng \(ABCD\) là hình thang vuông có hai đáy là \(AD\) và \(BC\), chiều cao là \(AB\).
Ta có \(AB = 3 - 1 = 2\), \(AD = 2\) và \(BC = 4\). Do đó diện tích hình thang \(ABCD\) là:
\(S\left( 3 \right) = \frac{{\left( {2 + 4} \right).2}}{2} = 6\).
b) Tương tự câu a, nhưng hoành độ của \(B\) là \(x\), ta suy ra tung độ của \(C\) là \(x + 1\).
Ta có \(AB = x - 1\), \(AD = 2\), \(BC = x + 1\). Do đó diện tích hình thang \(ABCD\) là:
\(S\left( x \right) = \frac{{\left( {AD + BC} \right).AB}}{2} = \frac{{\left( {2 + x + 1} \right)\left( {x - 1} \right)}}{2} = \frac{{\left( {x + 3} \right)\left( {x - 1} \right)}}{2} = \frac{{{x^2} + 2x - 3}}{2}\)
c) Ta có \(S'\left( x \right) = \frac{{2x + 2}}{2} = x + 1 = f\left( x \right)\). Vậy \(S\left( x \right)\) là một nguyên hàm của \(f\left( x \right)\).
d) Do \(F\left( x \right)\) là một nguyên hàm của \(f\left( x \right)\), ta có:
\(F\left( x \right) = \int {f\left( x \right)dx} = \int {\left( {x + 1} \right)dx} = \frac{{{x^2}}}{2} + x + C\)
Suy ra \(F\left( 3 \right) = \frac{{{3^2}}}{2} + 3 + C = \frac{{15}}{2} + C\) và \(F\left( 1 \right) = \frac{{{1^2}}}{2} + 1 + C = \frac{3}{2} + C\)
Như vậy ta có \(F\left( 3 \right) - F\left( 1 \right) = \left( {\frac{{15}}{2} + C} \right) - \left( {\frac{3}{2} + C} \right) = 6 = S\left( 3 \right)\).
Do đó, để tính \(S\left( 3 \right)\) khi biết một nguyên hàm của \(f\left( x \right)\), ta thực hiện tính nguyên hàm \(F\left( x \right)\) của \(f\left( x \right)\), sau đó ta tính \(F\left( 3 \right)\) và \(F\left( 1 \right)\), từ đó tính được \(S\left( 3 \right) = F\left( 3 \right) - F\left( 1 \right)\).
Trả lời câu hỏi Thực hành 1 trang 13 SGK Toán 12 Chân trời sáng tạo
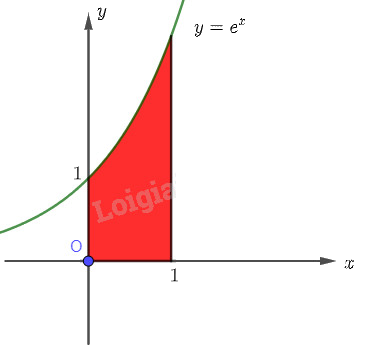
Tính diện tích hình thang cong giới hạn bởi đồ thị hàm số \(y = f\left( x \right) = {e^x}\), trục hoành, trục tung và đường thẳng \(x = 1\).
Phương pháp giải:
Tìm một nguyên hàm \(F\left( x \right)\) của hàm số \(f\left( x \right)\), sau đó sử dụng công thức để tính diện tích hình thang cong \(S = F\left( b \right) - F\left( a \right)\).
Lời giải chi tiết:
Ta có hàm số \(y = f\left( x \right) = {e^x}\) liên tục và dương trên đoạn \(\left[ {0;1} \right]\).
Ta có \(\int {f\left( x \right)dx} = \int {{e^x}dx} = {e^x} + C\), từ đó suy ra \(F\left( x \right) = {e^x}\) là một nguyên hàm của \(f\left( x \right) = {e^x}\).
Diện tích hình thang cong cần tính là: \(S = F\left( 1 \right) - F\left( 0 \right) = {e^1} - {e^0} = e - 1\).
Mục 1 của chương trình Toán 12 tập 2, Chân trời sáng tạo thường tập trung vào một chủ đề quan trọng, đặt nền móng cho các kiến thức tiếp theo. Việc nắm vững nội dung và phương pháp giải các bài tập trong mục này là vô cùng cần thiết. Bài viết này sẽ đi sâu vào phân tích từng bài tập trong trang 12 và 13, cung cấp lời giải chi tiết, kèm theo các lưu ý quan trọng để giúp các em hiểu rõ bản chất vấn đề.
Trang 12 thường chứa các bài tập vận dụng kiến thức cơ bản về một khái niệm mới. Các bài tập này thường có dạng trắc nghiệm hoặc tự luận đơn giản, nhằm kiểm tra mức độ hiểu bài của học sinh. Chúng ta sẽ cùng nhau giải từng bài tập, phân tích các bước giải và đưa ra kết luận chính xác.
Giả sử bài tập yêu cầu tính đạo hàm của một hàm số. Chúng ta sẽ sử dụng các quy tắc đạo hàm cơ bản, như quy tắc lũy thừa, quy tắc tích, quy tắc thương, và quy tắc hàm hợp để tìm ra kết quả. Quan trọng là phải ghi nhớ đúng công thức và áp dụng một cách linh hoạt.
Nếu bài tập yêu cầu tìm cực trị của hàm số, chúng ta cần tìm các điểm dừng của hàm số, sau đó xét dấu đạo hàm bậc nhất để xác định xem đó là điểm cực đại hay cực tiểu. Việc vẽ đồ thị hàm số cũng có thể giúp chúng ta hình dung rõ hơn về cực trị của hàm số.
Trang 13 thường chứa các bài tập nâng cao hơn, đòi hỏi học sinh phải vận dụng kiến thức một cách sáng tạo và linh hoạt. Các bài tập này có thể liên quan đến việc giải phương trình, bất phương trình, hoặc chứng minh một đẳng thức. Chúng ta sẽ cùng nhau khám phá các phương pháp giải khác nhau và tìm ra lời giải tối ưu.
Giả sử bài tập yêu cầu giải một phương trình lượng giác. Chúng ta có thể sử dụng các công thức lượng giác cơ bản, như công thức cộng, trừ, nhân, chia góc, và các công thức biến đổi lượng giác để đưa phương trình về dạng đơn giản hơn. Việc sử dụng đường tròn lượng giác cũng có thể giúp chúng ta tìm ra các nghiệm của phương trình.
Nếu bài tập yêu cầu chứng minh một đẳng thức, chúng ta cần biến đổi một hoặc cả hai vế của đẳng thức để đưa chúng về cùng dạng. Việc sử dụng các tính chất của phép toán và các công thức đại số có thể giúp chúng ta chứng minh đẳng thức một cách dễ dàng.
Để học tập môn Toán hiệu quả, các em cần:
Hy vọng rằng bài viết này đã cung cấp cho các em những kiến thức và kỹ năng cần thiết để giải các bài tập trong mục 1 trang 12 và 13 SGK Toán 12 tập 2, Chân trời sáng tạo. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!
| Bài tập | Lời giải |
|---|---|
| Bài 1 | (Lời giải chi tiết) |
| Bài 2 | (Lời giải chi tiết) |
| Bài 3 | (Lời giải chi tiết) |
| Bài 4 | (Lời giải chi tiết) |