Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tại giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2 trang 77, 78, 79 sách giáo khoa Toán 12 tập 2 chương trình Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Khảo sát thị lực của 100 học sinh, ta thu được bảng số liệu sau: Chọn ngẫu nhiên 1 bạn trong 100 học sinh trên. a) Biết rằng bạn đó có tật khúc xạ, tính xác suất bạn đó là học sinh nam. b) Biết rằng bạn đó là học sinh nam, tính xác suất bạn đó có tật khúc xạ.
Trả lời câu hỏi Vận dụng trang 79 SGK Toán 12 Chân trời sáng tạo
Người ta điều tra thấy ở một địa phương nọ có 2% tài xế sử dụng điện thoại di động khi lái xe. Trong các vụ tai nạn ở địa phương đó, người ta nhận thấy có 10% là do tài xế có sử dụng điện thoại khi lái xe gây ra. Hỏi việc sử dụng điện thoại di động khi lái xe làm tăng xác suất gây tai nạn lên bao nhiêu lần?
Phương pháp giải:
Gọi \(A\) là biến cố “Tài xế gây tai nạn”, \(B\) là biến cố “Tài xế có sử dụng điện thoại di động”. Ta cần so sánh \(P\left( {A|B} \right)\) và \(P\left( {A|\bar B} \right)\). Sử dụng công thức xác suất toàn phần và công thức Bayes, từ đó kết luận.
Lời giải chi tiết:
Gọi \(A\) là biến cố “Tài xế gây tai nạn”, \(B\) là biến cố “Tài xế có sử dụng điện thoại di động”. Suy ra \(P\left( {A|B} \right)\) là xác suất tài xế gây tai nạn khi sử dụng điện thoại, và \(P\left( {A|\bar B} \right)\) là xác suất tài xế gây tai nạn khi không sử dụng điện thoại.
Theo đề bài ta có \(P\left( B \right) = 0,02\), \(P\left( {B|A} \right) = 0,1\), suy ra \(P\left( {\bar B} \right) = 1 - 0,02 = 0,98\) và \(P\left( {\bar B|A} \right) = 1 - 0,1 = 0,9\).
Áp dụng công thức xác suất toàn phần, ta có
\(P\left( A \right) = P\left( B \right).P\left( {A|B} \right) + P\left( {\bar B} \right).P\left( {A|\bar B} \right) = 0,02.P\left( {A|B} \right) + 0,98.P\left( {A|\bar B} \right)\)
Mặt khác, theo công thức Bayes ta có
\(P\left( {B|A} \right) = \frac{{P\left( B \right).P\left( {A|B} \right)}}{{P\left( A \right)}} \Rightarrow P\left( A \right) = \frac{{P\left( B \right).P\left( {A|B} \right)}}{{P\left( {B|A} \right)}} = \frac{{0,02.P\left( {A|B} \right)}}{{0,1}} = 0,2.P\left( {A|B} \right)\)
Suy ra
\(0,2.P\left( {A|B} \right) = 0,02.P\left( {A|B} \right) + 0,98P\left( {A|\bar B} \right) \Rightarrow 0,18.P\left( {A|B} \right) = 0,98.P\left( {A|\bar B} \right)\)
Vậy \(\frac{{P\left( {A|B} \right)}}{{P\left( {A|\bar B} \right)}} = \frac{{0,98}}{{0,18}} = \frac{{49}}{9} \approx 5,4\). Điều đó có nghĩa khi sử dụng điện thoại, xác suất tài xế gây tai nạn khi lái xe sẽ tăng khoảng 5,4 lần.
Trả lời câu hỏi Hoạt động 2 trang 77 SGK Toán 12 Chân trời sáng tạo
Khảo sát thị lực của 100 học sinh, ta thu được bảng số liệu sau:
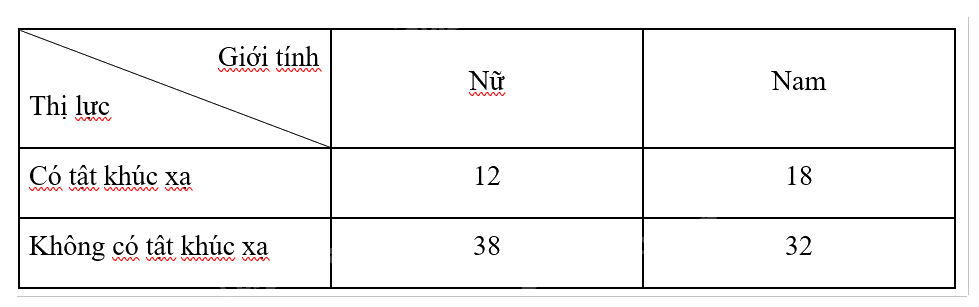
Chọn ngẫu nhiên 1 bạn trong 100 học sinh trên.
a) Biết rằng bạn đó có tật khúc xạ, tính xác suất bạn đó là học sinh nam.
b) Biết rằng bạn đó là học sinh nam, tính xác suất bạn đó có tật khúc xạ.
Phương pháp giải:
a) Tính số bạn bị tật khúc xạ, sau đó tính xác suất chọn được 1 bạn nam trong số những bạn bị tật khúc xạ.
b) Tính tổng số bạn nam, sau đó tính xác suất chọn được 1 bạn bị tật khúc xạ trong số những bạn nam.
Lời giải chi tiết:
a) Có tất cả \(12 + 18 = 30\) bạn bị tật khúc xạ, trong đó có 18 bạn nam. Vậy xác suất của biến cố là \(\frac{{18}}{{30}} = 0,6\).
b) Có tất cả \(18 + 32 = 50\) bạn nam, trong đó có 18 bạn bị tật khúc xạ. Vậy xác suất của biến cố là \(\frac{{18}}{{50}} = 0,36\).
Trả lời câu hỏi Thực hành 2 trang 79 SGK Toán 12 Chân trời sáng tạo
Khi phát hiện một vật thể bay, xác suất một hệ thống radar phát cảnh báo là 0,9 nếu vật thể bay đó là mục tiêu thật và là 0,05 nếu đó là mục tiêu giả. Có 99% các vật thể bay là mục tiêu giả. Biết rằng hệ thống radar đang phát cảnh báo khi phát hiện một vật thể bay. Tính xác suất vật thể đó là mục tiêu thật.

Phương pháp giải:
Gọi \(A\) là biến cố “Radar phát cảnh báo”, \(B\) là biến cố “Vật thể bay là mục tiêu thật”.
Xác suất cần tính là \(P\left( {B|A} \right)\). Theo đề bài, xác định \(P\left( A \right)\), \(P\left( B \right)\) và \(P\left( {A|B} \right)\), rồi sử dụng công thức Bayes.
Lời giải chi tiết:
Gọi \(A\) là biến cố “Radar phát cảnh báo”, \(B\) là biến cố “Vật thể bay là mục tiêu thật”.
Xác suất cần tính là \(P\left( {B|A} \right)\).
Theo đề bài, ta có \(P\left( {A|B} \right) = 0,9\); \(P\left( {A|\bar B} \right) = 0,05\); \(P\left( B \right) = 1 - 0,99 = 0,01\) và \(P\left( {\bar B} \right) = 0,99\).
Áp dụng công thức tính xác suất toàn phần, ta có:
\(P\left( A \right) = P\left( B \right)P\left( {A|B} \right) + P\left( {\bar B} \right)P\left( {A|\bar B} \right) = 0,01.0,9 + 0,99.0,05 = 0,0585.\)
Vậy khi radar phát cảnh báo, xác suất vật thể đó là mục tiêu thật là:
\(P\left( {B|A} \right) = \frac{{P\left( B \right).P\left( {A|B} \right)}}{{P\left( A \right)}} = \frac{{0,01.0,9}}{{0,0585}} = \frac{2}{{13}}.\)
Trả lời câu hỏi Hoạt động 2 trang 77 SGK Toán 12 Chân trời sáng tạo
Khảo sát thị lực của 100 học sinh, ta thu được bảng số liệu sau:
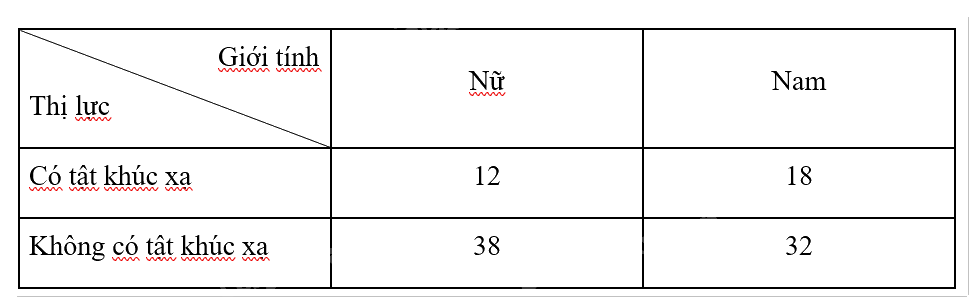
Chọn ngẫu nhiên 1 bạn trong 100 học sinh trên.
a) Biết rằng bạn đó có tật khúc xạ, tính xác suất bạn đó là học sinh nam.
b) Biết rằng bạn đó là học sinh nam, tính xác suất bạn đó có tật khúc xạ.
Phương pháp giải:
a) Tính số bạn bị tật khúc xạ, sau đó tính xác suất chọn được 1 bạn nam trong số những bạn bị tật khúc xạ.
b) Tính tổng số bạn nam, sau đó tính xác suất chọn được 1 bạn bị tật khúc xạ trong số những bạn nam.
Lời giải chi tiết:
a) Có tất cả \(12 + 18 = 30\) bạn bị tật khúc xạ, trong đó có 18 bạn nam. Vậy xác suất của biến cố là \(\frac{{18}}{{30}} = 0,6\).
b) Có tất cả \(18 + 32 = 50\) bạn nam, trong đó có 18 bạn bị tật khúc xạ. Vậy xác suất của biến cố là \(\frac{{18}}{{50}} = 0,36\).
Trả lời câu hỏi Thực hành 2 trang 79 SGK Toán 12 Chân trời sáng tạo
Khi phát hiện một vật thể bay, xác suất một hệ thống radar phát cảnh báo là 0,9 nếu vật thể bay đó là mục tiêu thật và là 0,05 nếu đó là mục tiêu giả. Có 99% các vật thể bay là mục tiêu giả. Biết rằng hệ thống radar đang phát cảnh báo khi phát hiện một vật thể bay. Tính xác suất vật thể đó là mục tiêu thật.

Phương pháp giải:
Gọi \(A\) là biến cố “Radar phát cảnh báo”, \(B\) là biến cố “Vật thể bay là mục tiêu thật”.
Xác suất cần tính là \(P\left( {B|A} \right)\). Theo đề bài, xác định \(P\left( A \right)\), \(P\left( B \right)\) và \(P\left( {A|B} \right)\), rồi sử dụng công thức Bayes.
Lời giải chi tiết:
Gọi \(A\) là biến cố “Radar phát cảnh báo”, \(B\) là biến cố “Vật thể bay là mục tiêu thật”.
Xác suất cần tính là \(P\left( {B|A} \right)\).
Theo đề bài, ta có \(P\left( {A|B} \right) = 0,9\); \(P\left( {A|\bar B} \right) = 0,05\); \(P\left( B \right) = 1 - 0,99 = 0,01\) và \(P\left( {\bar B} \right) = 0,99\).
Áp dụng công thức tính xác suất toàn phần, ta có:
\(P\left( A \right) = P\left( B \right)P\left( {A|B} \right) + P\left( {\bar B} \right)P\left( {A|\bar B} \right) = 0,01.0,9 + 0,99.0,05 = 0,0585.\)
Vậy khi radar phát cảnh báo, xác suất vật thể đó là mục tiêu thật là:
\(P\left( {B|A} \right) = \frac{{P\left( B \right).P\left( {A|B} \right)}}{{P\left( A \right)}} = \frac{{0,01.0,9}}{{0,0585}} = \frac{2}{{13}}.\)
Trả lời câu hỏi Vận dụng trang 79 SGK Toán 12 Chân trời sáng tạo
Người ta điều tra thấy ở một địa phương nọ có 2% tài xế sử dụng điện thoại di động khi lái xe. Trong các vụ tai nạn ở địa phương đó, người ta nhận thấy có 10% là do tài xế có sử dụng điện thoại khi lái xe gây ra. Hỏi việc sử dụng điện thoại di động khi lái xe làm tăng xác suất gây tai nạn lên bao nhiêu lần?
Phương pháp giải:
Gọi \(A\) là biến cố “Tài xế gây tai nạn”, \(B\) là biến cố “Tài xế có sử dụng điện thoại di động”. Ta cần so sánh \(P\left( {A|B} \right)\) và \(P\left( {A|\bar B} \right)\). Sử dụng công thức xác suất toàn phần và công thức Bayes, từ đó kết luận.
Lời giải chi tiết:
Gọi \(A\) là biến cố “Tài xế gây tai nạn”, \(B\) là biến cố “Tài xế có sử dụng điện thoại di động”. Suy ra \(P\left( {A|B} \right)\) là xác suất tài xế gây tai nạn khi sử dụng điện thoại, và \(P\left( {A|\bar B} \right)\) là xác suất tài xế gây tai nạn khi không sử dụng điện thoại.
Theo đề bài ta có \(P\left( B \right) = 0,02\), \(P\left( {B|A} \right) = 0,1\), suy ra \(P\left( {\bar B} \right) = 1 - 0,02 = 0,98\) và \(P\left( {\bar B|A} \right) = 1 - 0,1 = 0,9\).
Áp dụng công thức xác suất toàn phần, ta có
\(P\left( A \right) = P\left( B \right).P\left( {A|B} \right) + P\left( {\bar B} \right).P\left( {A|\bar B} \right) = 0,02.P\left( {A|B} \right) + 0,98.P\left( {A|\bar B} \right)\)
Mặt khác, theo công thức Bayes ta có
\(P\left( {B|A} \right) = \frac{{P\left( B \right).P\left( {A|B} \right)}}{{P\left( A \right)}} \Rightarrow P\left( A \right) = \frac{{P\left( B \right).P\left( {A|B} \right)}}{{P\left( {B|A} \right)}} = \frac{{0,02.P\left( {A|B} \right)}}{{0,1}} = 0,2.P\left( {A|B} \right)\)
Suy ra
\(0,2.P\left( {A|B} \right) = 0,02.P\left( {A|B} \right) + 0,98P\left( {A|\bar B} \right) \Rightarrow 0,18.P\left( {A|B} \right) = 0,98.P\left( {A|\bar B} \right)\)
Vậy \(\frac{{P\left( {A|B} \right)}}{{P\left( {A|\bar B} \right)}} = \frac{{0,98}}{{0,18}} = \frac{{49}}{9} \approx 5,4\). Điều đó có nghĩa khi sử dụng điện thoại, xác suất tài xế gây tai nạn khi lái xe sẽ tăng khoảng 5,4 lần.
Mục 2 của SGK Toán 12 tập 2 chương trình Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết hiệu quả các bài tập trong mục này, học sinh cần nắm vững lý thuyết, công thức và phương pháp giải liên quan. Bài viết này sẽ đi sâu vào từng bài tập, cung cấp lời giải chi tiết và phân tích các bước thực hiện.
Đề bài: (Giả định một đề bài cụ thể ở trang 77)
Lời giải: (Giải chi tiết bài tập 1, bao gồm các bước thực hiện, công thức sử dụng và kết luận)
Đề bài: (Giả định một đề bài cụ thể ở trang 77)
Lời giải: (Giải chi tiết bài tập 2, bao gồm các bước thực hiện, công thức sử dụng và kết luận)
Đề bài: (Giả định một đề bài cụ thể ở trang 78)
Lời giải: (Giải chi tiết bài tập 3, bao gồm các bước thực hiện, công thức sử dụng và kết luận)
Đề bài: (Giả định một đề bài cụ thể ở trang 78)
Lời giải: (Giải chi tiết bài tập 4, bao gồm các bước thực hiện, công thức sử dụng và kết luận)
Đề bài: (Giả định một đề bài cụ thể ở trang 79)
Lời giải: (Giải chi tiết bài tập 5, bao gồm các bước thực hiện, công thức sử dụng và kết luận)
Đề bài: (Giả định một đề bài cụ thể ở trang 79)
Lời giải: (Giải chi tiết bài tập 6, bao gồm các bước thực hiện, công thức sử dụng và kết luận)
Để hiểu sâu hơn về chủ đề này, các em có thể tham khảo thêm các tài liệu sau:
Hy vọng rằng bài viết này đã cung cấp cho các em những kiến thức và kỹ năng cần thiết để giải quyết các bài tập trong mục 2 trang 77, 78, 79 SGK Toán 12 tập 2 chương trình Chân trời sáng tạo. Chúc các em học tập tốt!