Chào mừng bạn đến với bài học về Lý thuyết Vecto và các phép toán trong không gian, một phần quan trọng của chương trình Toán 12 Chân trời sáng tạo. Bài học này sẽ cung cấp cho bạn những kiến thức nền tảng vững chắc về vecto, các phép toán trên vecto và ứng dụng của chúng trong không gian.
Chúng tôi tại giaitoan.edu.vn cam kết mang đến cho bạn trải nghiệm học tập trực tuyến hiệu quả và thú vị nhất, với các bài giảng được trình bày rõ ràng, dễ hiểu và nhiều bài tập thực hành để bạn có thể áp dụng kiến thức vào giải quyết các bài toán cụ thể.
Bài 1. Vecto và các phép toán trong không gian 1. Vecto trong không gian
1. Vecto trong không gian
|
2. Tổng và hiệu của hai vecto
a) Tổng của hai vecto
Trong không gian, cho hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \). Lấy một điểm A bất kì và các điểm B,C sao cho \(\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {BC} = \overrightarrow b \). Khi đó, vecto \(\overrightarrow {AC} \) được gọi là tổng của hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \), kí hiệu là \(\overrightarrow a + \overrightarrow b \) Phép lấy tổng của hai vecto được gọi là phép cộng vecto
|
b) Hiệu của hai vecto
Trong không gian, cho hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \). Hiệu của hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \) là tổng của hai vecto \(\mathop a\limits^ \to \) và vecto đối của \(\mathop b\limits^ \to \), kí hiệu là \(\mathop a\limits^ \to - \mathop b\limits^ \to \) Phép lấy hiệu của hai vecto được gọi là phép trừ vecto Với ba điểm O, A, B trong không gian, ta có: \(\overrightarrow {OA} - \overrightarrow {OB} = \overrightarrow {BA} \) (Quy tắc hiệu) |
3. Tích của một số với một vecto
Trong không gian, tích của một số thực \(k \ne 0\) với một vecto \(\overrightarrow a \ne \overrightarrow 0 \) là một vecto, kí hiệu là \(k\overrightarrow a \), được xác định như sau: - Cùng hướng với vecto \(\mathop a\limits^ \to \) nếu k > 0; ngược hướng với vecto \(\mathop a\limits^ \to \) nếu k < 0 - Có độ dài bằng \(\left| k \right|.\left| {\overrightarrow a } \right|\) Phép lấy tích của một số với một vecto được gọi là phép nhân một số với một vecto |
4. Tích vô hướng của hai vecto
a) Góc giữa hai vecto trong không gian
| Trong không gian, cho hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \) khác \(\mathop 0\limits^ \to \). Lấy một điểm O bất kỳ và gọi A, B là hai điểm sao cho \(\overrightarrow {OA} = \overrightarrow a ,\overrightarrow {OB} = \overrightarrow b \). Khi đó, góc \(\widehat {AOB}({0^ \circ } \le \widehat {AOB} \le {180^ \circ })\) được gọi là góc giữa hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \), kí hiệu \(\left( {\overrightarrow a ,\overrightarrow b } \right)\) |
b) Tích vô hướng của hai vecto
Trong không gian, cho hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \) khác \(\mathop 0\limits^ \to \). Tích vô hướng của hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \) là một số, kí hiệu là \(\overrightarrow a \cdot \overrightarrow b \), được xác định bởi công thức \(\overrightarrow a \cdot \overrightarrow b = \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right| \cdot \cos \left( {\overrightarrow a ,\overrightarrow b } \right)\) |
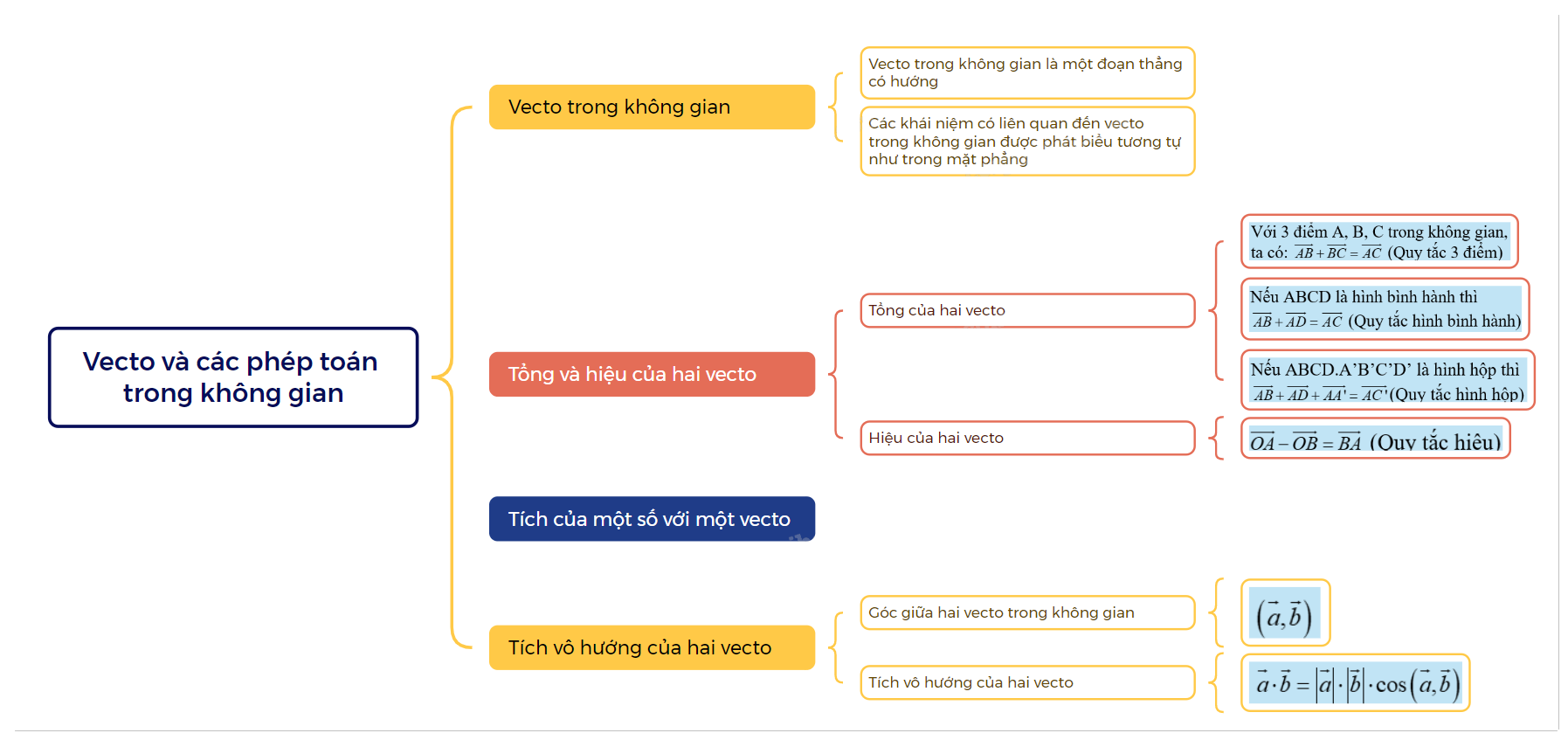
Trong chương trình Toán 12 Chân trời sáng tạo, phần Lý thuyết Vecto và các phép toán trong không gian đóng vai trò then chốt trong việc xây dựng nền tảng kiến thức về hình học không gian. Bài viết này sẽ cung cấp một cái nhìn tổng quan và chi tiết về các khái niệm, định lý và ứng dụng quan trọng của vecto trong không gian.
Vectơ là một đoạn thẳng có hướng. Nó được xác định bởi độ dài và hướng. Trong không gian, một vectơ được biểu diễn bằng một bộ ba số thực (x, y, z), gọi là tọa độ của vectơ. Vectơ có thể được sử dụng để biểu diễn các đại lượng vật lý như lực, vận tốc, gia tốc, và các đại lượng hình học như vị trí, hướng.
Có ba phép toán cơ bản trên vectơ: cộng, trừ và nhân với một số thực.
Tích vô hướng của hai vectơ a = (x1, y1, z1) và b = (x2, y2, z2) được định nghĩa là a ⋅ b = x1x2 + y1y2 + z1z2. Tích vô hướng có nhiều ứng dụng quan trọng, bao gồm:
Tích có hướng của hai vectơ a = (x1, y1, z1) và b = (x2, y2, z2) là một vectơ c = (x, y, z), được tính như sau:
c = a x b = (y1z2 - z1y2, z1x2 - x1z2, x1y2 - y1x2)
Tích có hướng có nhiều ứng dụng quan trọng, bao gồm:
Vectơ được sử dụng rộng rãi trong nhiều lĩnh vực của khoa học và kỹ thuật, bao gồm:
Bài tập 1: Cho a = (1, 2, 3) và b = (4, 5, 6). Tính a + b, a - b và 2a.
Bài tập 2: Cho a = (1, 0, 0) và b = (0, 1, 0). Tính a ⋅ b và a x b.
Lý thuyết Vecto và các phép toán trong không gian là một phần quan trọng của chương trình Toán 12 Chân trời sáng tạo. Việc nắm vững các khái niệm và định lý trong bài học này sẽ giúp bạn giải quyết các bài toán hình học không gian một cách hiệu quả và tự tin hơn. Hãy luyện tập thường xuyên và áp dụng kiến thức vào thực tế để đạt được kết quả tốt nhất.