Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 3, trang 60, 61 và 62 của sách giáo khoa Toán 12 tập 1 - Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Vận dụng
Trả lời câu hỏi Thực hành 3 trang 61 SGK Toán 12 Chân trời sáng tạo
Cho ba điểm M(7; –2; 0), N(–9; 0; 4), P(0; –6; 5).
a) Tìm toạ độ của các vectơ \(\overrightarrow {MN} ,\overrightarrow {NP} ,\overrightarrow {MP} \)
b) Tính các độ dài MN, NP, MP.
Phương pháp giải:
a) Cho hai vectơ \(\overrightarrow a = ({a_1};{a_2};{a_3})\), \(\overrightarrow b = ({b_1};{b_2};{b_3})\), ta có \(\overrightarrow a - \overrightarrow b = ({a_1} - {b_1};{a_2} - {b_2};{a_3} - {b_3})\)
b) Công thức tính độ lớn vecto: \(|\overrightarrow a | = \sqrt {{a_1}^2 + {a_2}^2 + {a_3}^2} \)
Lời giải chi tiết:
a) \(\overrightarrow {MN} = ( - 9 - 7;0 - ( - 2);4 - 0) = ( - 16;2;4)\)
\(\overrightarrow {NP} = (0 - ( - 9); - 6 - 0;5 - 4) = (9; - 6;1)\)
\(\overrightarrow {MP} = (0 - 7; - 6 - ( - 2);5 - 0) = ( - 7; - 4;5)\)
b) \(MN = \sqrt {{{( - 16)}^2} + {2^2} + {4^2}} = 2\sqrt {69} \)
\(NP = \sqrt {{9^2} + {{( - 6)}^2} + {1^2}} = \sqrt {118} \)
\(MP = \sqrt {{{( - 7)}^2} + {{( - 4)}^2} + {5^2}} = 3\sqrt {10} \)
Trả lời câu hỏi Khám phá 3 trang 60 SGK Toán 12 Chân trời sáng tạo
Cho hai điểm \(A({x_A};{y_A};{z_A}),B({x_B};{y_B};{z_B})\). Từ biểu thức \(\overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {OA} \), tìm toạ độ của vectơ \(\overrightarrow {AB} \) theo toạ độ hai điểm A, B.
Phương pháp giải:
Cho hai vectơ \(\overrightarrow a = ({a_1};{a_2};{a_3})\), \(\overrightarrow b = ({b_1};{b_2};{b_3})\), ta có \(\overrightarrow a - \overrightarrow b = ({a_1} - {b_1};{a_2} - {b_2};{a_3} - {b_3})\)
Lời giải chi tiết:
\(\overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {OA} = ({x_A};{y_A};{z_A}) - ({x_B};{y_B};{z_B}) = ({x_A} - {x_B};{y_A} - {y_B};{z_A} - {z_B})\)
Trả lời câu hỏi Khám phá 4 trang 61 SGK Toán 12 Chân trời sáng tạo
Cho tam giác ABC có \(A({x_A};{y_A};{z_A}),B({x_B};{y_B};{z_B}),C({x_C};{y_C};{z_C})\). Gọi \(M({x_M};{y_M};{z_M})\) là trung điểm của đoạn thẳng AB và \(G({x_G};{y_G};{z_G})\) là trọng tâm của tam giác ABC. Sử dụng các hệ thức vectơ \(\overrightarrow {OM} = \frac{1}{2}(\overrightarrow {OA} + \overrightarrow {OB} )\),\(\overrightarrow {OG} = \frac{1}{3}(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} )\), tìm toạ độ của các điểm M và G.
Phương pháp giải:
Cho hai vectơ \(\overrightarrow a = ({a_1};{a_2};{a_3})\), \(\overrightarrow b = ({b_1};{b_2};{b_3})\), ta có \(\overrightarrow a + \overrightarrow b = ({a_1} + {b_1};{a_2} + {b_2};{a_3} + {b_3})\)
Lời giải chi tiết:
\(\overrightarrow {OA} + \overrightarrow {OB} = ({x_A} + {x_B};{y_A} + {y_B};{z_A} + {z_B})\)
\(\overrightarrow {OM} = \frac{1}{2}({x_A} + {x_B};{y_A} + {y_B};{z_A} + {z_B}) = (\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2};\frac{{{z_A} + {z_B}}}{2})\)=> \(M(\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2};\frac{{{z_A} + {z_B}}}{2})\)
\(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = {x_A} + {x_B} + {x_C};{y_A} + {y_B} + {y_C};{z_A} + {z_B} + {z_C}\)
\(\overrightarrow {OG} = \frac{1}{3}(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} ) = \frac{1}{3}({x_A} + {x_B} + {x_C};{y_A} + {y_B} + {y_C};{z_A} + {z_B} + {z_C}) = (\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3};\frac{{{z_A} + {z_B} + {z_C}}}{3})\)=> \(G(\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3};\frac{{{z_A} + {z_B} + {z_C}}}{3})\)
Trả lời câu hỏi Thực hành 4 trang 62 SGK Toán 12 Chân trời sáng tạo
Cho tam giác MNP có M(2; 1; 3), N(1; 2; 3), P(–3; –1; 0). Tìm toạ độ:
a) Các điểm M′, N′, P′ lần lượt là trung điểm của các cạnh NP, MP, MN;
b) Trọng tâm G của tam giác M′N′P′.
Phương pháp giải:
Cho tam giác ABC có \(A({a_1};{a_2};{a_3})\), \(B({b_1};{b_2};{b_3})\), \(C({c_1};{c_2};{c_3})\), ta có \(M(\frac{{{a_1} + {b_1}}}{2};\frac{{{a_2} + {b_2}}}{2};\frac{{{a_3} + {b_3}}}{2})\) là trung điểm của AB, \(G(\frac{{{a_1} + {b_1} + {c_1}}}{3};\frac{{{a_2} + {b_2} + {c_2}}}{3};\frac{{{a_3} + {b_3} + {c_3}}}{3})\) là trọng tâm của tam giác ABC
Lời giải chi tiết:
a) \(M'(\frac{{1 - 3}}{2};\frac{{2 - 1}}{2};\frac{3}{2})\) hay \(M'( - 1;\frac{1}{2};\frac{3}{2})\)
\(N'(\frac{{2 - 3}}{2};\frac{{1 - 1}}{2};\frac{3}{2})\) hay \(N'( - \frac{1}{2};0;\frac{3}{2})\).
\(P'(\frac{{2 + 1}}{2};\frac{{1 + 2}}{2};\frac{{3 + 3}}{2})\) hay \(P'(\frac{3}{2};\frac{3}{2};3)\)
b) \(G(\frac{{2 + 1 - 3}}{3};\frac{{1 + 2 - 1}}{3};\frac{{3 + 3 + 0}}{3})\) hay \(G(0;\frac{2}{3};1)\)
Trả lời câu hỏi Thực hành 5 trang 63 SGK Toán 12 Chân trời sáng tạo
Cho tam giác MNP có M(0; 1; 2), N(5; 9; 3), P(7; 8; 2).
a) Tìm toạ độ điểm K là chân đường cao kẻ từ M của tam giác MNP.
b) Tìm độ dài cạnh MN và MP.
c) Tính góc M
Phương pháp giải:
a)\(\overrightarrow a \bot \overrightarrow b \Rightarrow \overrightarrow a .\overrightarrow b = 0\)
b) Công thức tính độ lớn vecto: \(|\overrightarrow a | = \sqrt {{a_1}^2 + {a_2}^2 + {a_3}^2} \)
c) \(\cos (\overrightarrow a ,\overrightarrow b ) = \frac{{\overrightarrow a .\overrightarrow b }}{{|\overrightarrow a |.|\overrightarrow b |}}\)
Lời giải chi tiết:
a) Ta có: \(\overrightarrow {NP} = (2; - 1; - 1)\)
Gọi K(x;y;z) là chân đường cao kẻ từ M của tam giác MNP
=> \(\overrightarrow {NK} = (x - 5;y - 9;z - 3)\)
\(\overrightarrow {NK} \) cùng phương với \(\overrightarrow {NP} \) nên \(x - 5 = 2t;y - 9 = - t;z - 3 = - t\) => \(K(2t + 2; - t + 9; - t + 3)\)
Ta có: \(\overrightarrow {MK} = (2t + 2; - t + 8; - t + 1)\)
\(\overrightarrow {MK} \bot \overrightarrow {NP} \Leftrightarrow \overrightarrow {MK} .\overrightarrow {NP} = 0 \Leftrightarrow (2t + 2).2 - ( - t + 8) - ( - t + 1) = 0 \Leftrightarrow t = \frac{5}{6}\)
Vậy \(K(\frac{{11}}{3};\frac{{49}}{6};\frac{{13}}{6})\)
b) Ta có: \(\overrightarrow {MN} = (5;8;1) \Rightarrow MN = \sqrt {{5^2} + {8^2} + {1^2}} = 3\sqrt {10} \)
\(\overrightarrow {MP} = (7;7;0) \Rightarrow MP = \sqrt {{7^2} + {7^2}} = 7\sqrt 2 \)
c) \(\cos M = \frac{{\overrightarrow {MN} .\overrightarrow {MP} }}{{|\overrightarrow {MN} |.|\overrightarrow {MP} |}} = \frac{{5.7 + 8.7}}{{3\sqrt {10} .7\sqrt 2 }} = \frac{{13\sqrt 5 }}{{30}}\)
Trả lời câu hỏi Vận dụng 4 trang 64 SGK Toán 12 Chân trời sáng tạo
Trên phần mềm mô phỏng việc điều khiển drone giao hàng trong không gian Oxyz, một đội gồm ba drone giao hàng A, B, C đang có toạ độ là A(1; 1; 1), B(5; 7; 9), C(9; 11 ; 4). Tính:
a) Các khoảng cách giữa mỗi cặp drone giao hàng.
b) Góc \(\widehat {BAC}\)
Phương pháp giải:
a) Công thức tính độ lớn vecto: \(|\overrightarrow a | = \sqrt {{a_1}^2 + {a_2}^2 + {a_3}^2} \)
b) \(\cos (\overrightarrow a ,\overrightarrow b ) = \frac{{\overrightarrow a .\overrightarrow b }}{{|\overrightarrow a |.|\overrightarrow b |}}\)
Lời giải chi tiết:
a) \(\overrightarrow {AB} = (4;6;8) \Rightarrow AB = \sqrt {{4^2} + {6^2} + {8^2}} = 2\sqrt {29} \)
\(\overrightarrow {AC} = (8;10;3) \Rightarrow \sqrt {{8^2} + {{10}^2} + {3^2}} = \sqrt {173} \)
\(\overrightarrow {BC} = (4;4; - 5) \Rightarrow \sqrt {{4^2} + {4^2} + {{( - 5)}^2}} = \sqrt {57} \)
c) \(\cos \widehat {BAC} = \frac{{\overrightarrow {AB} .\overrightarrow {AC} }}{{|\overrightarrow {AB} |.|\overrightarrow {AC} |}} = \frac{{4.8 + 6.10 + 8.3}}{{2\sqrt {29} .\sqrt {173} }} \approx 0,82 \Rightarrow \widehat {BAC} = 35,03^\circ \)
Trả lời câu hỏi Khám phá 3 trang 60 SGK Toán 12 Chân trời sáng tạo
Trả lời câu hỏi Khám phá 3 trang 60 SGK Toán 12 Chân trời sáng tạo
Cho hai điểm \(A({x_A};{y_A};{z_A}),B({x_B};{y_B};{z_B})\). Từ biểu thức \(\overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {OA} \), tìm toạ độ của vectơ \(\overrightarrow {AB} \) theo toạ độ hai điểm A, B.
Phương pháp giải:
Cho hai vectơ \(\overrightarrow a = ({a_1};{a_2};{a_3})\), \(\overrightarrow b = ({b_1};{b_2};{b_3})\), ta có \(\overrightarrow a - \overrightarrow b = ({a_1} - {b_1};{a_2} - {b_2};{a_3} - {b_3})\)
Lời giải chi tiết:
\(\overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {OA} = ({x_A};{y_A};{z_A}) - ({x_B};{y_B};{z_B}) = ({x_A} - {x_B};{y_A} - {y_B};{z_A} - {z_B})\)
Trả lời câu hỏi Thực hành 3 trang 61 SGK Toán 12 Chân trời sáng tạo
Cho ba điểm M(7; –2; 0), N(–9; 0; 4), P(0; –6; 5).
a) Tìm toạ độ của các vectơ \(\overrightarrow {MN} ,\overrightarrow {NP} ,\overrightarrow {MP} \)
b) Tính các độ dài MN, NP, MP.
Phương pháp giải:
a) Cho hai vectơ \(\overrightarrow a = ({a_1};{a_2};{a_3})\), \(\overrightarrow b = ({b_1};{b_2};{b_3})\), ta có \(\overrightarrow a - \overrightarrow b = ({a_1} - {b_1};{a_2} - {b_2};{a_3} - {b_3})\)
b) Công thức tính độ lớn vecto: \(|\overrightarrow a | = \sqrt {{a_1}^2 + {a_2}^2 + {a_3}^2} \)
Lời giải chi tiết:
a) \(\overrightarrow {MN} = ( - 9 - 7;0 - ( - 2);4 - 0) = ( - 16;2;4)\)
\(\overrightarrow {NP} = (0 - ( - 9); - 6 - 0;5 - 4) = (9; - 6;1)\)
\(\overrightarrow {MP} = (0 - 7; - 6 - ( - 2);5 - 0) = ( - 7; - 4;5)\)
b) \(MN = \sqrt {{{( - 16)}^2} + {2^2} + {4^2}} = 2\sqrt {69} \)
\(NP = \sqrt {{9^2} + {{( - 6)}^2} + {1^2}} = \sqrt {118} \)
\(MP = \sqrt {{{( - 7)}^2} + {{( - 4)}^2} + {5^2}} = 3\sqrt {10} \)
Trả lời câu hỏi Khám phá 4 trang 61 SGK Toán 12 Chân trời sáng tạo
Cho tam giác ABC có \(A({x_A};{y_A};{z_A}),B({x_B};{y_B};{z_B}),C({x_C};{y_C};{z_C})\). Gọi \(M({x_M};{y_M};{z_M})\) là trung điểm của đoạn thẳng AB và \(G({x_G};{y_G};{z_G})\) là trọng tâm của tam giác ABC. Sử dụng các hệ thức vectơ \(\overrightarrow {OM} = \frac{1}{2}(\overrightarrow {OA} + \overrightarrow {OB} )\),\(\overrightarrow {OG} = \frac{1}{3}(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} )\), tìm toạ độ của các điểm M và G.
Phương pháp giải:
Cho hai vectơ \(\overrightarrow a = ({a_1};{a_2};{a_3})\), \(\overrightarrow b = ({b_1};{b_2};{b_3})\), ta có \(\overrightarrow a + \overrightarrow b = ({a_1} + {b_1};{a_2} + {b_2};{a_3} + {b_3})\)
Lời giải chi tiết:
\(\overrightarrow {OA} + \overrightarrow {OB} = ({x_A} + {x_B};{y_A} + {y_B};{z_A} + {z_B})\)
\(\overrightarrow {OM} = \frac{1}{2}({x_A} + {x_B};{y_A} + {y_B};{z_A} + {z_B}) = (\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2};\frac{{{z_A} + {z_B}}}{2})\)=> \(M(\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2};\frac{{{z_A} + {z_B}}}{2})\)
\(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = {x_A} + {x_B} + {x_C};{y_A} + {y_B} + {y_C};{z_A} + {z_B} + {z_C}\)
\(\overrightarrow {OG} = \frac{1}{3}(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} ) = \frac{1}{3}({x_A} + {x_B} + {x_C};{y_A} + {y_B} + {y_C};{z_A} + {z_B} + {z_C}) = (\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3};\frac{{{z_A} + {z_B} + {z_C}}}{3})\)=> \(G(\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3};\frac{{{z_A} + {z_B} + {z_C}}}{3})\)
Trả lời câu hỏi Thực hành 4 trang 62 SGK Toán 12 Chân trời sáng tạo
Cho tam giác MNP có M(2; 1; 3), N(1; 2; 3), P(–3; –1; 0). Tìm toạ độ:
a) Các điểm M′, N′, P′ lần lượt là trung điểm của các cạnh NP, MP, MN;
b) Trọng tâm G của tam giác M′N′P′.
Phương pháp giải:
Cho tam giác ABC có \(A({a_1};{a_2};{a_3})\), \(B({b_1};{b_2};{b_3})\), \(C({c_1};{c_2};{c_3})\), ta có \(M(\frac{{{a_1} + {b_1}}}{2};\frac{{{a_2} + {b_2}}}{2};\frac{{{a_3} + {b_3}}}{2})\) là trung điểm của AB, \(G(\frac{{{a_1} + {b_1} + {c_1}}}{3};\frac{{{a_2} + {b_2} + {c_2}}}{3};\frac{{{a_3} + {b_3} + {c_3}}}{3})\) là trọng tâm của tam giác ABC
Lời giải chi tiết:
a) \(M'(\frac{{1 - 3}}{2};\frac{{2 - 1}}{2};\frac{3}{2})\) hay \(M'( - 1;\frac{1}{2};\frac{3}{2})\)
\(N'(\frac{{2 - 3}}{2};\frac{{1 - 1}}{2};\frac{3}{2})\) hay \(N'( - \frac{1}{2};0;\frac{3}{2})\).
\(P'(\frac{{2 + 1}}{2};\frac{{1 + 2}}{2};\frac{{3 + 3}}{2})\) hay \(P'(\frac{3}{2};\frac{3}{2};3)\)
b) \(G(\frac{{2 + 1 - 3}}{3};\frac{{1 + 2 - 1}}{3};\frac{{3 + 3 + 0}}{3})\) hay \(G(0;\frac{2}{3};1)\)
Trả lời câu hỏi Vận dụng 3 trang 62 SGK Toán 12 Chân trời sáng tạo
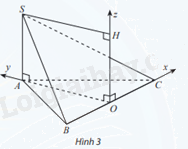
Cho hình chóp S.ABC có \(SA \bot (ABC)\), SA = a và đáy ABC là tam giác đều cạnh a, O là trung điểm của BC. Bằng cách thiết lập hệ toạ độ như hình vẽ, hãy tìm toạ độ:
a) Các điểm A, S, B, C
b) Trung điểm M của SB và trung điểm N của SC;
c) Trọng tâm G của tam giác SBC
Phương pháp giải:
\(\overrightarrow {OA} = (a;b;c) \Rightarrow A(a;b;c)\). Cho tam giác ABC có \(A({a_1};{a_2};{a_3})\), \(B({b_1};{b_2};{b_3})\), \(C({c_1};{c_2};{c_3})\), ta có \(M(\frac{{{a_1} + {b_1}}}{2};\frac{{{a_2} + {b_2}}}{2};\frac{{{a_3} + {b_3}}}{2})\) là trung điểm của AB, \(G(\frac{{{a_1} + {b_1} + {c_1}}}{3};\frac{{{a_2} + {b_2} + {c_2}}}{3};\frac{{{a_3} + {b_3} + {c_3}}}{3})\) là trọng tâm của tam giác ABC
Lời giải chi tiết:
a) \(OA = \sqrt {A{B^2} - O{B^2}} = \sqrt {{a^2} - {{(\frac{a}{2})}^2}} = \frac{{a\sqrt 3 }}{2}\)
\(\overrightarrow {OA} = \frac{{a\sqrt 3 }}{2}\overrightarrow j = (0;\frac{{a\sqrt 3 }}{2};0) \Rightarrow A(0;\frac{{a\sqrt 3 }}{2};0)\)
\(\overrightarrow {OB} = - \frac{a}{2}\overrightarrow i = ( - \frac{a}{2};0;0) \Rightarrow B( - \frac{a}{2};0;0)\)
\(\overrightarrow {OC} = \frac{a}{2}\overrightarrow i = (\frac{a}{2};0;0) \Rightarrow C(\frac{a}{2};0;0)\)
\(\overrightarrow {OS} = \frac{{a\sqrt 3 }}{2}\overrightarrow j + a\overrightarrow k = (0;\frac{{a\sqrt 3 }}{2};a) \Rightarrow S(0;\frac{{a\sqrt 3 }}{2};a)\)
b) \(M(\frac{{0 - \frac{a}{2}}}{2};\frac{{\frac{{a\sqrt 3 }}{2}}}{2};\frac{a}{2})\) hay \(M( - \frac{a}{2};\frac{{a\sqrt 3 }}{4};\frac{a}{2})\)
\(N(\frac{{0 + \frac{a}{2}}}{2};\frac{{\frac{{a\sqrt 3 }}{2}}}{2};\frac{a}{2})\) hay \(N(\frac{a}{2};\frac{{a\sqrt 3 }}{4};\frac{a}{2})\)
c) \(G(\frac{{0 + \frac{a}{2} - \frac{a}{2}}}{3};\frac{{\frac{{a\sqrt 3 }}{2}}}{3};\frac{a}{3})\) hay \(G(0;\frac{{a\sqrt 3 }}{6};\frac{a}{3})\)
Trả lời câu hỏi Thực hành 5 trang 63 SGK Toán 12 Chân trời sáng tạo
Cho tam giác MNP có M(0; 1; 2), N(5; 9; 3), P(7; 8; 2).
a) Tìm toạ độ điểm K là chân đường cao kẻ từ M của tam giác MNP.
b) Tìm độ dài cạnh MN và MP.
c) Tính góc M
Phương pháp giải:
a)\(\overrightarrow a \bot \overrightarrow b \Rightarrow \overrightarrow a .\overrightarrow b = 0\)
b) Công thức tính độ lớn vecto: \(|\overrightarrow a | = \sqrt {{a_1}^2 + {a_2}^2 + {a_3}^2} \)
c) \(\cos (\overrightarrow a ,\overrightarrow b ) = \frac{{\overrightarrow a .\overrightarrow b }}{{|\overrightarrow a |.|\overrightarrow b |}}\)
Lời giải chi tiết:
a) Ta có: \(\overrightarrow {NP} = (2; - 1; - 1)\)
Gọi K(x;y;z) là chân đường cao kẻ từ M của tam giác MNP
=> \(\overrightarrow {NK} = (x - 5;y - 9;z - 3)\)
\(\overrightarrow {NK} \) cùng phương với \(\overrightarrow {NP} \) nên \(x - 5 = 2t;y - 9 = - t;z - 3 = - t\) => \(K(2t + 2; - t + 9; - t + 3)\)
Ta có: \(\overrightarrow {MK} = (2t + 2; - t + 8; - t + 1)\)
\(\overrightarrow {MK} \bot \overrightarrow {NP} \Leftrightarrow \overrightarrow {MK} .\overrightarrow {NP} = 0 \Leftrightarrow (2t + 2).2 - ( - t + 8) - ( - t + 1) = 0 \Leftrightarrow t = \frac{5}{6}\)
Vậy \(K(\frac{{11}}{3};\frac{{49}}{6};\frac{{13}}{6})\)
b) Ta có: \(\overrightarrow {MN} = (5;8;1) \Rightarrow MN = \sqrt {{5^2} + {8^2} + {1^2}} = 3\sqrt {10} \)
\(\overrightarrow {MP} = (7;7;0) \Rightarrow MP = \sqrt {{7^2} + {7^2}} = 7\sqrt 2 \)
c) \(\cos M = \frac{{\overrightarrow {MN} .\overrightarrow {MP} }}{{|\overrightarrow {MN} |.|\overrightarrow {MP} |}} = \frac{{5.7 + 8.7}}{{3\sqrt {10} .7\sqrt 2 }} = \frac{{13\sqrt 5 }}{{30}}\)
Trả lời câu hỏi Vận dụng 4 trang 64 SGK Toán 12 Chân trời sáng tạo
Trên phần mềm mô phỏng việc điều khiển drone giao hàng trong không gian Oxyz, một đội gồm ba drone giao hàng A, B, C đang có toạ độ là A(1; 1; 1), B(5; 7; 9), C(9; 11 ; 4). Tính:
a) Các khoảng cách giữa mỗi cặp drone giao hàng.
b) Góc \(\widehat {BAC}\)
Phương pháp giải:
a) Công thức tính độ lớn vecto: \(|\overrightarrow a | = \sqrt {{a_1}^2 + {a_2}^2 + {a_3}^2} \)
b) \(\cos (\overrightarrow a ,\overrightarrow b ) = \frac{{\overrightarrow a .\overrightarrow b }}{{|\overrightarrow a |.|\overrightarrow b |}}\)
Lời giải chi tiết:
a) \(\overrightarrow {AB} = (4;6;8) \Rightarrow AB = \sqrt {{4^2} + {6^2} + {8^2}} = 2\sqrt {29} \)
\(\overrightarrow {AC} = (8;10;3) \Rightarrow \sqrt {{8^2} + {{10}^2} + {3^2}} = \sqrt {173} \)
\(\overrightarrow {BC} = (4;4; - 5) \Rightarrow \sqrt {{4^2} + {4^2} + {{( - 5)}^2}} = \sqrt {57} \)
c) \(\cos \widehat {BAC} = \frac{{\overrightarrow {AB} .\overrightarrow {AC} }}{{|\overrightarrow {AB} |.|\overrightarrow {AC} |}} = \frac{{4.8 + 6.10 + 8.3}}{{2\sqrt {29} .\sqrt {173} }} \approx 0,82 \Rightarrow \widehat {BAC} = 35,03^\circ \)
Trả lời câu hỏi Vận dụng 3 trang 62 SGK Toán 12 Chân trời sáng tạo
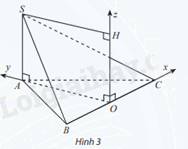
Cho hình chóp S.ABC có \(SA \bot (ABC)\), SA = a và đáy ABC là tam giác đều cạnh a, O là trung điểm của BC. Bằng cách thiết lập hệ toạ độ như hình vẽ, hãy tìm toạ độ:
a) Các điểm A, S, B, C
b) Trung điểm M của SB và trung điểm N của SC;
c) Trọng tâm G của tam giác SBC
Phương pháp giải:
\(\overrightarrow {OA} = (a;b;c) \Rightarrow A(a;b;c)\). Cho tam giác ABC có \(A({a_1};{a_2};{a_3})\), \(B({b_1};{b_2};{b_3})\), \(C({c_1};{c_2};{c_3})\), ta có \(M(\frac{{{a_1} + {b_1}}}{2};\frac{{{a_2} + {b_2}}}{2};\frac{{{a_3} + {b_3}}}{2})\) là trung điểm của AB, \(G(\frac{{{a_1} + {b_1} + {c_1}}}{3};\frac{{{a_2} + {b_2} + {c_2}}}{3};\frac{{{a_3} + {b_3} + {c_3}}}{3})\) là trọng tâm của tam giác ABC
Lời giải chi tiết:
a) \(OA = \sqrt {A{B^2} - O{B^2}} = \sqrt {{a^2} - {{(\frac{a}{2})}^2}} = \frac{{a\sqrt 3 }}{2}\)
\(\overrightarrow {OA} = \frac{{a\sqrt 3 }}{2}\overrightarrow j = (0;\frac{{a\sqrt 3 }}{2};0) \Rightarrow A(0;\frac{{a\sqrt 3 }}{2};0)\)
\(\overrightarrow {OB} = - \frac{a}{2}\overrightarrow i = ( - \frac{a}{2};0;0) \Rightarrow B( - \frac{a}{2};0;0)\)
\(\overrightarrow {OC} = \frac{a}{2}\overrightarrow i = (\frac{a}{2};0;0) \Rightarrow C(\frac{a}{2};0;0)\)
\(\overrightarrow {OS} = \frac{{a\sqrt 3 }}{2}\overrightarrow j + a\overrightarrow k = (0;\frac{{a\sqrt 3 }}{2};a) \Rightarrow S(0;\frac{{a\sqrt 3 }}{2};a)\)
b) \(M(\frac{{0 - \frac{a}{2}}}{2};\frac{{\frac{{a\sqrt 3 }}{2}}}{2};\frac{a}{2})\) hay \(M( - \frac{a}{2};\frac{{a\sqrt 3 }}{4};\frac{a}{2})\)
\(N(\frac{{0 + \frac{a}{2}}}{2};\frac{{\frac{{a\sqrt 3 }}{2}}}{2};\frac{a}{2})\) hay \(N(\frac{a}{2};\frac{{a\sqrt 3 }}{4};\frac{a}{2})\)
c) \(G(\frac{{0 + \frac{a}{2} - \frac{a}{2}}}{3};\frac{{\frac{{a\sqrt 3 }}{2}}}{3};\frac{a}{3})\) hay \(G(0;\frac{{a\sqrt 3 }}{6};\frac{a}{3})\)
Mục 3 của chương trình Toán 12 tập 1 - Chân trời sáng tạo tập trung vào việc nghiên cứu về giới hạn của hàm số. Đây là một khái niệm nền tảng quan trọng trong giải tích, giúp học sinh hiểu rõ hơn về hành vi của hàm số khi biến số tiến tới một giá trị nhất định. Việc nắm vững kiến thức về giới hạn là bước đệm quan trọng để học sinh tiếp cận các khái niệm phức tạp hơn như đạo hàm và tích phân.
Trang 60 SGK Toán 12 tập 1 - Chân trời sáng tạo chứa các bài tập vận dụng kiến thức về khái niệm giới hạn để tính giới hạn của các hàm số đơn giản. Các bài tập này thường yêu cầu học sinh áp dụng định nghĩa giới hạn và các tính chất của giới hạn để tìm ra kết quả.
Ví dụ, bài tập 1 yêu cầu tính giới hạn của hàm số f(x) = 2x + 1 khi x tiến tới 2. Để giải bài tập này, ta có thể áp dụng định nghĩa giới hạn như sau:
lim (x->2) (2x + 1) = 2 * 2 + 1 = 5
Trang 61 SGK Toán 12 tập 1 - Chân trời sáng tạo chứa các bài tập phức tạp hơn, yêu cầu học sinh vận dụng kiến thức về giới hạn một bên và các tính chất của giới hạn để giải quyết. Các bài tập này thường liên quan đến các hàm số có chứa giá trị tuyệt đối hoặc các hàm số không xác định tại một điểm.
Ví dụ, bài tập 2 yêu cầu tính giới hạn của hàm số f(x) = |x - 1| / (x - 1) khi x tiến tới 1. Để giải bài tập này, ta cần xét giới hạn bên trái và giới hạn bên phải của hàm số.
lim (x->1+) |x - 1| / (x - 1) = 1
lim (x->1-) |x - 1| / (x - 1) = -1
Vì giới hạn bên trái và giới hạn bên phải không bằng nhau, nên giới hạn của hàm số tại x = 1 không tồn tại.
Trang 62 SGK Toán 12 tập 1 - Chân trời sáng tạo chứa các bài tập tổng hợp, yêu cầu học sinh vận dụng tất cả các kiến thức đã học về giới hạn để giải quyết. Các bài tập này thường có tính ứng dụng cao và giúp học sinh rèn luyện kỹ năng giải toán một cách toàn diện.
Ví dụ, bài tập 3 yêu cầu chứng minh rằng lim (x->0) sin(x) / x = 1. Để chứng minh điều này, ta có thể sử dụng định lý kẹp (squeeze theorem).
Hy vọng rằng với lời giải chi tiết và những lời khuyên hữu ích trên đây, các em học sinh sẽ tự tin hơn khi giải các bài tập về giới hạn trong SGK Toán 12 tập 1 - Chân trời sáng tạo. Chúc các em học tập tốt và đạt kết quả cao trong kỳ thi sắp tới!