Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 4, trang 30, 31 và 32 của sách giáo khoa Toán 12 tập 1, chương trình Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong các kỳ thi sắp tới.
Khảo sát hàm số \(y = \frac{{a{x^2} + bx + c}}{{mx + n}}(a \ne 0,m \ne 0\), đa thức tử không chia hết cho đa thức mẫu)
Trả lời câu hỏi Thực hành 3 trang 32 SGK Toán 12 Chân trời sáng tạo
Khảo sát và vẽ đồ thị của các hàm số sau:
a) \(y = x - \frac{1}{x}\)
b) \(y = - x + 2 - \frac{1}{{x + 1}}\)
c) \(y = \frac{{ - {x^2} - x + 2}}{{x + 1}}\)
Phương pháp giải:
Bước 1. Tìm tập xác định của hàm số
Bước 2. Xét sự biến thiên của hàm số
− Tìm đạo hàm y', xét dấu y', xác định khoảng đơn điệu, cực trị (nếu có) của hàm số.
− Tìm giới hạn tại vô cực, giới hạn vô cực của hàm số và các đường tiệm cận của đồ thị hàm số (nếu có).
− Lập bảng biến thiên của hàm số.
Bước 3. Vẽ đồ thị của hàm số
− Xác định các điểm cực trị (nếu có), giao điểm của đồ thị với các trục toạ độ
− Vẽ các đường tiệm cận của đồ thị hàm số (nếu có).
− Vẽ đồ thị hàm số.
Lời giải chi tiết:
a) \(y = x - \frac{1}{x}\)
Tập xác định: \(D = \mathbb{R}\backslash \{ 0\} \)
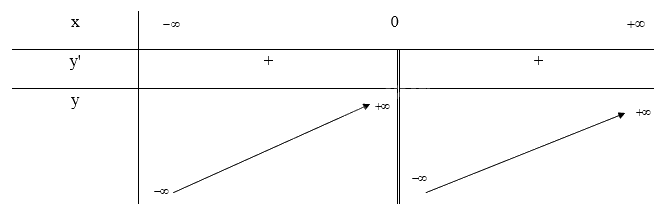
\(y' = 1 + \frac{1}{{{x^2}}} \ge 0\forall x \in D\) nên hàm số đồng biến trên D
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } (x - \frac{1}{x}) = + \infty ;\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } (x - \frac{1}{x}) = - \infty \)
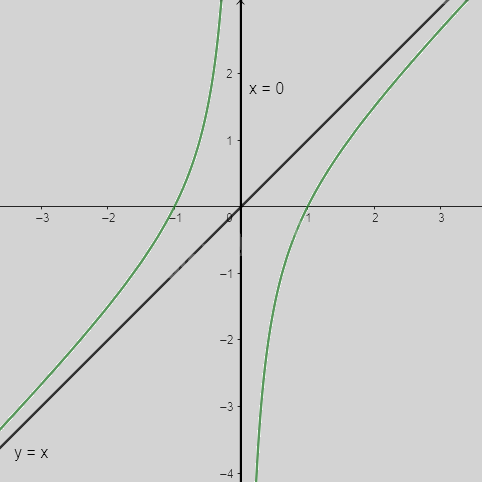
\(a = \mathop {\lim }\limits_{x \to + \infty } (1 - \frac{1}{{{x^2}}}) = 1;b = \mathop {\lim }\limits_{x \to + \infty } (x - \frac{1}{x} - x) = 0\) nên y = x là tiệm cận xiên của đồ thị hàm số
\(\mathop {\lim }\limits_{x \to {0^ + }} y = \mathop {\lim }\limits_{x \to {0^ + }} (x - \frac{1}{x}) = - \infty ;\mathop {\lim }\limits_{x \to {0^ - }} y = \mathop {\lim }\limits_{x \to {0^ - }} (x - \frac{1}{x}) = + \infty \) nên x = 0 là tiệm cận đứng của đồ thị hàm số
 Ta có: \(y = 0 \Leftrightarrow x - \frac{1}{x} = 0 \Leftrightarrow x = 1\)
Ta có: \(y = 0 \Leftrightarrow x - \frac{1}{x} = 0 \Leftrightarrow x = 1\)
Vậy đồ thị của hàm số giao với trục Ox tại điểm (1; 0)
b) \(y = - x + 2 - \frac{1}{{x + 1}}\)
Tập xác định: \(D = \mathbb{R}\backslash \{ - 1\} \)
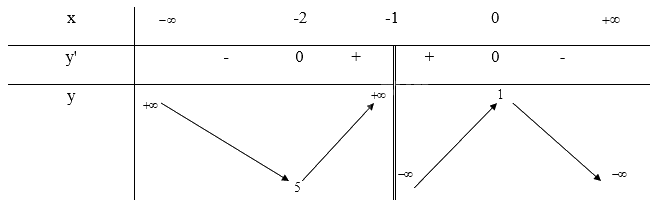
\(y' = - 1 + \frac{1}{{{{(x + 1)}^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 2\\x = 0\end{array} \right.\)
Trên các khoảng (\( - \infty \); -2), (0; \( + \infty \)) thì y' < 0 nên hàm số nghịch biến trên mỗi khoảng đó. Trên khoảng (-2; -1) và (-1; 0) thì y' > 0 nên hàm số đồng biến trên khoảng đó.
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } ( - x + 2 - \frac{1}{{x + 1}}) = - \infty ;\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } ( - x + 2 - \frac{1}{{x + 1}}) = + \infty \)
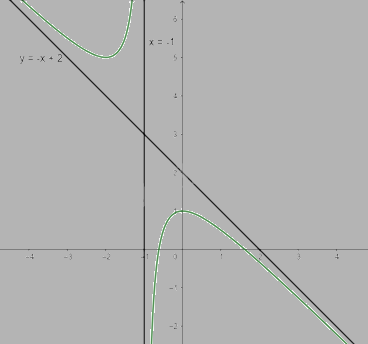
\(a = \mathop {\lim }\limits_{x \to + \infty } ( - 1 + \frac{2}{x} - \frac{1}{{{x^2} + x}}) = - 1;b = \mathop {\lim }\limits_{x \to + \infty } ( - x + 2 - \frac{1}{{x + 1}} + x) = 2\) nên y = -x + 2 là tiệm cận xiên của đồ thị hàm số
\(\mathop {\lim }\limits_{x \to - {1^ + }} y = \mathop {\lim }\limits_{x \to - {1^ + }} ( - x + 2 - \frac{1}{{x + 1}}) = - \infty ;\mathop {\lim }\limits_{x \to - {1^ - }} y = \mathop {\lim }\limits_{x \to - {1^ - }} ( - x + 2 - \frac{1}{{x + 1}}) = + \infty \) nên x = -1 là tiệm cận đứng của đồ thị hàm số
Khi x = 0 thì y = 1 nên (0;1) là giao điểm của y với trục Oy
Ta có: \(y = 0 \Leftrightarrow - x + 2 - \frac{1}{{x + 1}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = \frac{{1 - \sqrt 5 }}{2}\\x = \frac{{1 + \sqrt 5 }}{2}\end{array} \right.\)
Vậy đồ thị của hàm số giao với trục Ox tại điểm (\(\frac{{1 - \sqrt 5 }}{2}\); 0) và (\(\frac{{1 + \sqrt 5 }}{2}\);0)
Trả lời câu hỏi Thực hành 3 trang 32 SGK Toán 12 Chân trời sáng tạo
Khảo sát và vẽ đồ thị của các hàm số sau:
a) \(y = x - \frac{1}{x}\)
b) \(y = - x + 2 - \frac{1}{{x + 1}}\)
c) \(y = \frac{{ - {x^2} - x + 2}}{{x + 1}}\)
Phương pháp giải:
Bước 1. Tìm tập xác định của hàm số
Bước 2. Xét sự biến thiên của hàm số
− Tìm đạo hàm y', xét dấu y', xác định khoảng đơn điệu, cực trị (nếu có) của hàm số.
− Tìm giới hạn tại vô cực, giới hạn vô cực của hàm số và các đường tiệm cận của đồ thị hàm số (nếu có).
− Lập bảng biến thiên của hàm số.
Bước 3. Vẽ đồ thị của hàm số
− Xác định các điểm cực trị (nếu có), giao điểm của đồ thị với các trục toạ độ
− Vẽ các đường tiệm cận của đồ thị hàm số (nếu có).
− Vẽ đồ thị hàm số.
Lời giải chi tiết:
a) \(y = x - \frac{1}{x}\)
Tập xác định: \(D = \mathbb{R}\backslash \{ 0\} \)
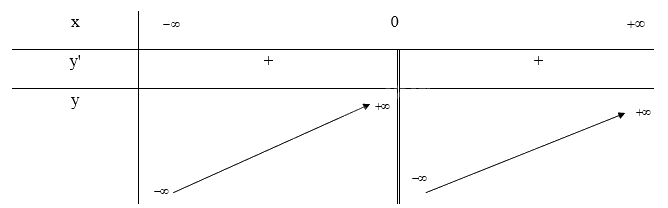
\(y' = 1 + \frac{1}{{{x^2}}} \ge 0\forall x \in D\) nên hàm số đồng biến trên D
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } (x - \frac{1}{x}) = + \infty ;\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } (x - \frac{1}{x}) = - \infty \)
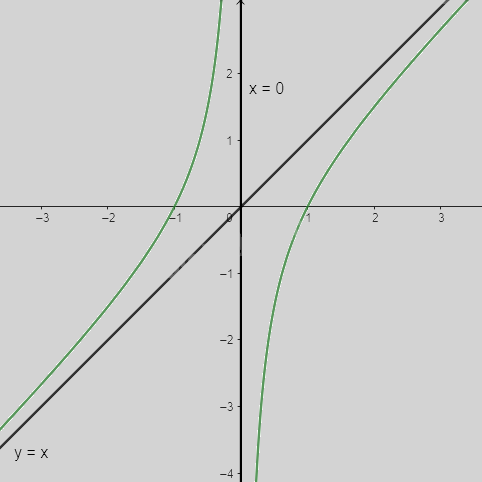
\(a = \mathop {\lim }\limits_{x \to + \infty } (1 - \frac{1}{{{x^2}}}) = 1;b = \mathop {\lim }\limits_{x \to + \infty } (x - \frac{1}{x} - x) = 0\) nên y = x là tiệm cận xiên của đồ thị hàm số
\(\mathop {\lim }\limits_{x \to {0^ + }} y = \mathop {\lim }\limits_{x \to {0^ + }} (x - \frac{1}{x}) = - \infty ;\mathop {\lim }\limits_{x \to {0^ - }} y = \mathop {\lim }\limits_{x \to {0^ - }} (x - \frac{1}{x}) = + \infty \) nên x = 0 là tiệm cận đứng của đồ thị hàm số
 Ta có: \(y = 0 \Leftrightarrow x - \frac{1}{x} = 0 \Leftrightarrow x = 1\)
Ta có: \(y = 0 \Leftrightarrow x - \frac{1}{x} = 0 \Leftrightarrow x = 1\)
Vậy đồ thị của hàm số giao với trục Ox tại điểm (1; 0)
b) \(y = - x + 2 - \frac{1}{{x + 1}}\)
Tập xác định: \(D = \mathbb{R}\backslash \{ - 1\} \)
\(y' = - 1 + \frac{1}{{{{(x + 1)}^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 2\\x = 0\end{array} \right.\)
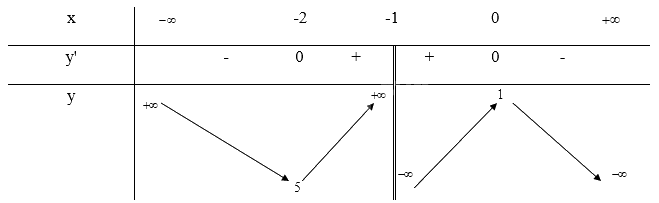
Trên các khoảng (\( - \infty \); -2), (0; \( + \infty \)) thì y' < 0 nên hàm số nghịch biến trên mỗi khoảng đó. Trên khoảng (-2; -1) và (-1; 0) thì y' > 0 nên hàm số đồng biến trên khoảng đó.
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } ( - x + 2 - \frac{1}{{x + 1}}) = - \infty ;\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } ( - x + 2 - \frac{1}{{x + 1}}) = + \infty \)
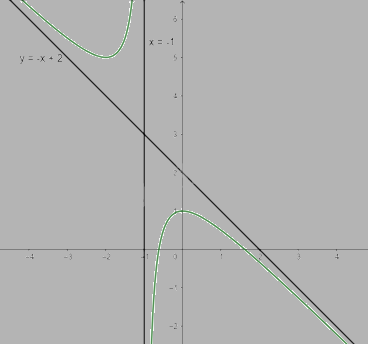
\(a = \mathop {\lim }\limits_{x \to + \infty } ( - 1 + \frac{2}{x} - \frac{1}{{{x^2} + x}}) = - 1;b = \mathop {\lim }\limits_{x \to + \infty } ( - x + 2 - \frac{1}{{x + 1}} + x) = 2\) nên y = -x + 2 là tiệm cận xiên của đồ thị hàm số
\(\mathop {\lim }\limits_{x \to - {1^ + }} y = \mathop {\lim }\limits_{x \to - {1^ + }} ( - x + 2 - \frac{1}{{x + 1}}) = - \infty ;\mathop {\lim }\limits_{x \to - {1^ - }} y = \mathop {\lim }\limits_{x \to - {1^ - }} ( - x + 2 - \frac{1}{{x + 1}}) = + \infty \) nên x = -1 là tiệm cận đứng của đồ thị hàm số
Khi x = 0 thì y = 1 nên (0;1) là giao điểm của y với trục Oy
Ta có: \(y = 0 \Leftrightarrow - x + 2 - \frac{1}{{x + 1}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = \frac{{1 - \sqrt 5 }}{2}\\x = \frac{{1 + \sqrt 5 }}{2}\end{array} \right.\)
Vậy đồ thị của hàm số giao với trục Ox tại điểm (\(\frac{{1 - \sqrt 5 }}{2}\); 0) và (\(\frac{{1 + \sqrt 5 }}{2}\);0)
Mục 4 của SGK Toán 12 tập 1 chương trình Chân trời sáng tạo tập trung vào các kiến thức về đạo hàm của hàm số. Đây là một phần quan trọng trong chương trình Toán 12, nền tảng cho việc giải quyết nhiều bài toán phức tạp hơn trong các chương tiếp theo và trong kỳ thi THPT Quốc gia. Việc nắm vững các khái niệm, định lý và kỹ năng liên quan đến đạo hàm là vô cùng cần thiết.
Mục 4 bao gồm các nội dung chính sau:
Trang 30 SGK Toán 12 tập 1 Chân trời sáng tạo thường chứa các bài tập vận dụng kiến thức về định nghĩa đạo hàm và đạo hàm của các hàm số đơn giản. Các bài tập này giúp học sinh làm quen với việc tính đạo hàm bằng định nghĩa và hiểu rõ ý nghĩa của đạo hàm trong việc xác định hệ số góc của tiếp tuyến.
Ví dụ: Bài 1 trang 30 yêu cầu tính đạo hàm của hàm số f(x) = x2 tại x = 2. Lời giải: Sử dụng định nghĩa đạo hàm, ta có:
f'(2) = limh→0 [f(2+h) - f(2)] / h = limh→0 [(2+h)2 - 22] / h = limh→0 [4 + 4h + h2 - 4] / h = limh→0 [4h + h2] / h = limh→0 (4 + h) = 4
Trang 31 tập trung vào việc áp dụng các quy tắc tính đạo hàm để tính đạo hàm của các hàm số phức tạp hơn. Các bài tập này đòi hỏi học sinh phải nắm vững các quy tắc và biết cách kết hợp chúng một cách linh hoạt.
Ví dụ: Bài 2 trang 31 yêu cầu tính đạo hàm của hàm số g(x) = 3x3 - 2x2 + 5x - 1. Lời giải: Sử dụng quy tắc tính đạo hàm của tổng và tích, ta có:
g'(x) = 9x2 - 4x + 5
Trang 32 thường chứa các bài tập về đạo hàm của các hàm số sơ cấp như hàm số mũ, hàm số logarit và hàm số lượng giác. Các bài tập này đòi hỏi học sinh phải nhớ các công thức đạo hàm của các hàm số này và biết cách áp dụng chúng vào giải toán.
Ví dụ: Bài 3 trang 32 yêu cầu tính đạo hàm của hàm số h(x) = ex + ln(x). Lời giải: Sử dụng công thức đạo hàm của hàm số mũ và hàm số logarit, ta có:
h'(x) = ex + 1/x
Hy vọng với lời giải chi tiết và hướng dẫn cụ thể trên đây, các em học sinh sẽ tự tin hơn trong việc giải các bài tập mục 4 trang 30, 31, 32 SGK Toán 12 tập 1 Chân trời sáng tạo. Chúc các em học tập tốt và đạt kết quả cao trong các kỳ thi sắp tới!