Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12 tập 1 - Chân trời sáng tạo. Bài viết này sẽ giúp bạn giải quyết triệt để bài tập 3 trang 24, nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, giúp bạn tiết kiệm thời gian và đạt kết quả cao trong môn Toán.
Tìm các tiệm cận của đồ thị hàm số sau: a) \(y = \frac{{2x - 3}}{{5{x^2} - 15x + 10}}\) b) \(y = \frac{{{x^2} + x - 1}}{x}\) c) \(y = \frac{{16{x^2} - 8x}}{{16{x^2} + 1}}\)
Đề bài
Tìm các tiệm cận của đồ thị hàm số sau:
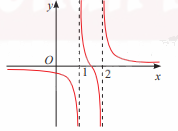
a) \(y = \frac{{2x - 3}}{{5{x^2} - 15x + 10}}\)
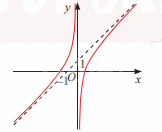
b) \(y = \frac{{{x^2} + x - 1}}{x}\)
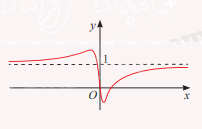
c) \(y = \frac{{16{x^2} - 8x}}{{16{x^2} + 1}}\)
Phương pháp giải - Xem chi tiết
Quan sát đồ thị
Lời giải chi tiết
a) Đường thẳng x = 1 và x = 2 là tiệm cận đứng của đồ thị hàm số \(y = \frac{{2x - 3}}{{5{x^2} - 15x + 10}}\)
Đường thẳng y = 0 là tiệm cận ngang của đồ thị hàm số \(y = \frac{{2x - 3}}{{5{x^2} - 15x + 10}}\)
b) Đường thẳng x = 0 là tiệm cận đứng của đồ thị hàm số \(y = \frac{{{x^2} + x - 1}}{x}\)
Đường thẳng y = \(x + 1\) là tiệm cận xiên của đồ thị hàm số \(y = \frac{{{x^2} + x - 1}}{x}\)
c) Đường thẳng y = 1 là tiệm cận ngang của đồ thị hàm số \(y = \frac{{16{x^2} - 8x}}{{16{x^2} + 1}}\)
Bài tập 3 trang 24 SGK Toán 12 tập 1 - Chân trời sáng tạo thuộc chương trình học về giới hạn của hàm số. Bài tập này yêu cầu học sinh vận dụng kiến thức về giới hạn một bên, giới hạn tại một điểm và các tính chất của giới hạn để giải quyết các bài toán cụ thể. Việc nắm vững kiến thức nền tảng và kỹ năng giải bài tập là vô cùng quan trọng để đạt kết quả tốt trong môn Toán.
Bài tập 3 bao gồm một số câu hỏi nhỏ, yêu cầu học sinh tính giới hạn của hàm số tại một điểm cho trước. Các hàm số có thể là hàm đa thức, hàm hữu tỉ hoặc hàm lượng giác. Để giải quyết bài tập này, học sinh cần:
Dưới đây là lời giải chi tiết cho từng câu hỏi trong bài tập 3 trang 24 SGK Toán 12 tập 1 - Chân trời sáng tạo:
Để tính giới hạn của hàm số tại một điểm, ta có thể sử dụng phương pháp thay trực tiếp giá trị của điểm đó vào hàm số. Nếu kết quả là một số thực, thì đó là giới hạn của hàm số tại điểm đó. Nếu kết quả là một biểu thức không xác định, ta cần sử dụng các kỹ thuật biến đổi đại số để đơn giản hóa biểu thức và tìm ra giới hạn.
Trong trường hợp hàm số không xác định tại điểm cần tính giới hạn, ta có thể sử dụng phương pháp tính giới hạn một bên. Phương pháp này cho phép ta tính giới hạn của hàm số khi x tiến tới điểm đó từ bên trái và bên phải. Nếu hai giới hạn một bên bằng nhau, thì đó là giới hạn của hàm số tại điểm đó.
Đối với các hàm số lượng giác, ta có thể sử dụng các công thức lượng giác và các giới hạn đặc biệt để tính giới hạn. Ví dụ, ta có giới hạn lim (sin x)/x = 1 khi x tiến tới 0.
Ngoài bài tập 3 trang 24, còn rất nhiều bài tập tương tự về giới hạn hàm số trong SGK Toán 12 tập 1 - Chân trời sáng tạo. Để giải quyết các bài tập này, học sinh cần nắm vững các kiến thức và kỹ năng sau:
Để học tập môn Toán hiệu quả, đặc biệt là phần giới hạn hàm số, bạn có thể áp dụng một số mẹo sau:
Bài tập 3 trang 24 SGK Toán 12 tập 1 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về giới hạn hàm số. Hy vọng rằng với lời giải chi tiết và các hướng dẫn trong bài viết này, bạn sẽ tự tin hơn trong quá trình học tập và đạt kết quả tốt trong môn Toán.
| Dạng bài tập | Phương pháp giải |
|---|---|
| Hàm đa thức | Thay trực tiếp giá trị |
| Hàm hữu tỉ | Rút gọn biểu thức, tính giới hạn một bên |
| Hàm lượng giác | Sử dụng công thức lượng giác, giới hạn đặc biệt |