Chủ đề Khảo sát và vẽ đồ thị hàm số là một phần quan trọng trong chương trình Toán 12 Chân trời sáng tạo. Việc nắm vững lý thuyết và kỹ năng này không chỉ giúp học sinh giải quyết các bài toán trong kỳ thi mà còn là nền tảng vững chắc cho các kiến thức toán học nâng cao.
Tại giaitoan.edu.vn, chúng tôi cung cấp tài liệu học tập đầy đủ, chi tiết và dễ hiểu về lý thuyết khảo sát và vẽ đồ thị các hàm số cơ bản như hàm bậc ba, hàm bậc bốn, hàm mũ, hàm logarit,...
1. Sơ đồ khảo sát hàm số Các bước khảo sát hàm số
1. Sơ đồ khảo sát hàm số
Các bước khảo sát hàm số
1. Tìm tập xác định của hàm số 2. Xét sự biến thiên của hàm số
3. Vẽ đồ thị của hàm số
|
2. Khảo sát hàm số \(y = a{x^3} + b{x^2} + cx + d(a \ne 0)\)
Ví dụ: Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y = - {x^3} + 3{x^2} - 4\)
1. Tập xác định của hàm số: R
2. Sự biến thiên:
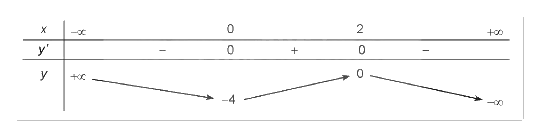
3. Đồ thị:
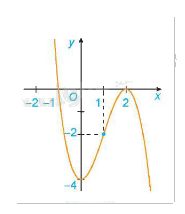
3. Khảo sát hàm số \(y = \frac{{ax + b}}{{cx + d}}(c \ne 0,ad - bc \ne 0)\)
Ví dụ: Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y = \frac{{x + 1}}{{x - 2}}\)
1. Tập xác định của hàm số: R\{2}
2. Sự biến thiên:
\(\mathop {\lim }\limits_{x \to {2^ - }} y = - \infty ;\mathop {\lim }\limits_{x \to {2^ + }} y = + \infty \)
Do đó, đồ thị của hàm số có tiệm cận đứng là x = 2, tiệm cận ngang là y = 1
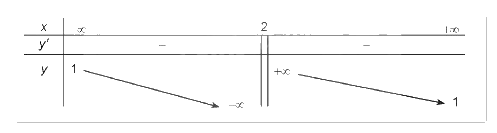
3. Đồ thị:
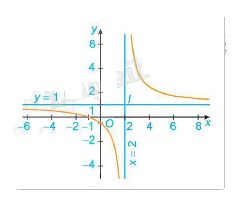
4. Khảo sát hàm số\(y = \frac{{a{x^2} + bx + c}}{{px + q}}(a \ne 0,p \ne 0)\)(đa thức tử không chia hết cho đa thức mẫu)
Ví dụ: Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y = \frac{{{x^2} - x - 1}}{{x - 2}}\)
1. Tập xác định của hàm số: R\{2}
2. Sự biến thiên: Viết \(y = x + 1 + \frac{1}{{x - 2}}\)
\(\mathop {\lim }\limits_{x \to {2^ - }} y = - \infty ;\mathop {\lim }\limits_{x \to {2^ + }} y = + \infty \)
\(\mathop {\lim }\limits_{x \to + \infty } \left[ {y - \left( {x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{{x - 2}} = 0\); \(\mathop {\lim }\limits_{x \to - \infty } \left[ {y - \left( {x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to - \infty } \frac{1}{{x - 2}} = 0\)
Do đó, đồ thị của hàm số có tiệm cận đứng là x = 2, tiệm cận xiên là y = x+1
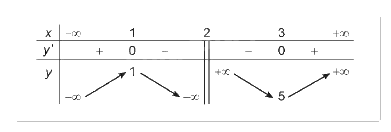
3. Đồ thị:
5. Vận dụng đạo hàm và khảo sát hàm số để giải quyết một số vấn đề liên quan đến thực tiễn
Ví dụ: Số dân của một thị trấn sau t năm kể từ năm 1970 được ước tính bởi công thức \(f(t) = \frac{{26t + 10}}{{t + 5}}\) (f(t) được tính bằng nghìn người)
a) Tính số dân của thị trấn vào năm 2022
b) Xem y = f(t) là một hàm số xác định trên nửa khoảng \(\left[ {0; + \infty } \right)\). Khảo sát sự biến thiên và vẽ đồ thị của hàm số f(t)
c) Đạo hàm của hàm số y = f(t) biểu thị tốc độ tăng dân số của thị trấn (tính bằng nghìn người/năm)
Giải:
a) Ta có: \(f(52) = \frac{{26.52 + 10}}{{52 + 5}} = \frac{{1362}}{{57}} \approx 23,895\) (nghìn người)
Vậy số dân của thị trấn vào năm 2022 khoảng 23895 nghìn người
b)
1) Sự biến thiên
\(\mathop {\lim }\limits_{t \to + \infty } f(t) = 26\). Do đó, đường thẳng y = 26 là tiệm cận ngang của đồ thị hàm số.
\(f'(t) = \frac{{120}}{{{{(t + 5)}^2}}} > 0\) với mọi \(t \ge 0\)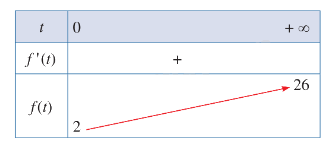
Hàm số đồng biến trên nửa khoảng \(\left[ {0; + \infty } \right)\).
Hàm số không có cực trị
2) Đồ thị
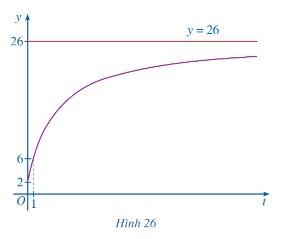
c)
\(f'(52) = \frac{{120}}{{{{(52 + 5)}^2}}} = \frac{{40}}{{1083}}\)
\(f'(t) = 0,192 \Leftrightarrow \frac{{120}}{{{{(t + 5)}^2}}} = 0,192 \Leftrightarrow {(t + 5)^2} = 625 \Leftrightarrow t = 20\) (do \(t \ge 0\))
Vậy vào năm 1990, tốc độ tăng dân số là 0,192 nghìn người/năm.
Chương trình Toán 12 Chân trời sáng tạo tập trung vào việc phát triển khả năng tư duy và ứng dụng toán học vào thực tế. Do đó, việc nắm vững phương pháp khảo sát hàm số và vẽ đồ thị đóng vai trò then chốt. Dưới đây là tổng hợp lý thuyết chi tiết và các bước thực hiện để bạn có thể tự tin giải quyết các bài toán liên quan.
Khảo sát hàm số là quá trình nghiên cứu các đặc điểm của hàm số, bao gồm:
Hàm số bậc ba có dạng: y = ax3 + bx2 + cx + d (a ≠ 0). Các bước khảo sát:
Hàm số bậc bốn có dạng: y = ax4 + bx3 + cx2 + dx + e (a ≠ 0). Quy trình khảo sát tương tự hàm số bậc ba, nhưng cần chú ý đến các trường hợp đặc biệt như:
Hàm số mũ: y = ax (a > 0, a ≠ 1)
Hàm số logarit: y = logax (a > 0, a ≠ 1)
Việc luyện tập thường xuyên với các bài tập khác nhau sẽ giúp bạn nắm vững phương pháp khảo sát hàm số và vẽ đồ thị một cách hiệu quả. Chúc bạn học tập tốt!
| Hàm số | Đạo hàm cấp nhất | Đạo hàm cấp hai |
|---|---|---|
| y = x3 - 3x2 + 2 | y' = 3x2 - 6x | y'' = 6x - 6 |
| y = x4 - 4x2 + 3 | y' = 4x3 - 8x | y'' = 12x2 - 8 |