Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 4 trang 48, 49, 50 SGK Toán 12 tập 1 chương trình Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập hiệu quả.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, tự tin giải quyết các bài toán Toán 12 và đạt kết quả cao trong học tập.
Tích vô hướng của hai vectơ
Trả lời câu hỏi Khám phá 5 trang 48 SGK Toán 12 Chân trời sáng tạo
a) Nhắc lại định nghĩa góc giữa hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) trong mặt phẳng.
b) Làm thế nào để định nghĩa góc giữa hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) trong không gian?
Phương pháp giải:
Nhớ lại định nghĩa đã học về góc giữa hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) trong mặt phẳng và suy luận ra góc giữa hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) trong không gian.
Lời giải chi tiết:
a) Trong mặt phẳng, cho hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) đều khác vectơ không. Từ một điểm A bất kỳ, gọi B và C là hai điểm sao cho \(\overrightarrow {AB} = \overrightarrow u \) và \(\overrightarrow {AC} = \overrightarrow v \). Khi đó góc \(\widehat {BAC}\) được gọi là góc giữa hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \).
b) Trong không gian, cho hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) đều khác vectơ không. Từ một điểm A bất kỳ, gọi B và C là hai điểm sao cho \(\overrightarrow {AB} = \overrightarrow u \) và \(\overrightarrow {AC} = \overrightarrow v \). Khi đó góc \(\widehat {BAC}\) được gọi là góc giữa hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \).
Trả lời câu hỏi Khám phá 6 trang 49 SGK Toán 12 Chân trời sáng tạo
Trong không gian, cho \(\overrightarrow u \) và \(\overrightarrow v \) thoả mãn \(|\overrightarrow u | = 2\) , \(|\overrightarrow v | = 3\). Lấy một điểm A bất kì, gọi B và C là hai điểm sao cho \(\overrightarrow {AB} = \overrightarrow u \), \(\overrightarrow {AC} = \overrightarrow v \) (Hình 24). Giả sử \(\widehat {BAC} = 60^\circ \)
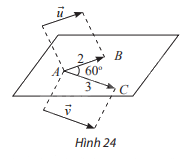
a) Tính góc \((\overrightarrow u ,\overrightarrow v )\)
b) Trong mặt phẳng (ABC), tính tích vô hướng \(\overrightarrow {AB} .\overrightarrow {AC} \)
Phương pháp giải:
a) Trong không gian, cho hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) đều khác vectơ không. Từ một điểm A bất kỳ, gọi B và C là hai điểm sao cho \(\overrightarrow {AB} = \overrightarrow u \) và \(\overrightarrow {AC} = \overrightarrow v \). Khi đó góc \(\widehat {BAC}\) được gọi là góc giữa hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \).
b) Công thức tính tích vô hướng của 2 vecto: \(\overrightarrow u .\overrightarrow v = |\overrightarrow u |.|\overrightarrow v |.\cos (\overrightarrow u ,\overrightarrow v )\)
Lời giải chi tiết:
a) Góc \((\overrightarrow u ,\overrightarrow v )\) = \(\widehat {BAC} = 60^\circ \)
b) \(\overrightarrow {AB} .\overrightarrow {AC} \) = \(AB.AC.\cos \widehat {BAC} = 2.3.\cos 60^\circ = 3\)
Trả lời câu hỏi Thực hành 8 trang 48 SGK Toán 12 Chân trời sáng tạo
Cho hình lập phương ABCD.A′B′C′D′. Xác định góc \((\overrightarrow {AC} ,\overrightarrow {B'D'} ),(\overrightarrow {A'A} ,\overrightarrow {CB'} )\)
Phương pháp giải:
Trong không gian, cho hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) đều khác vectơ không. Từ một điểm A bất kỳ, gọi B và C là hai điểm sao cho \(\overrightarrow {AB} = \overrightarrow u \) và \(\overrightarrow {AC} = \overrightarrow v \). Khi đó góc \(\widehat {BAC}\) được gọi là góc giữa hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \).
Lời giải chi tiết:
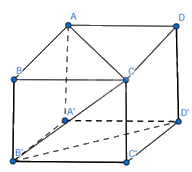
Góc \((\overrightarrow {AC} ,\overrightarrow {B'D'} )\) = góc \((\overrightarrow {AC} ,\overrightarrow {BD} )\) = \(90^\circ \) (góc giữa 2 đường chéo của hình vuông)
\((\overrightarrow {A'A} ,\overrightarrow {CB'} ) = (\overrightarrow {B'B} ,\overrightarrow {CB'} ) = {180^o} - (\overrightarrow {B'B} ,\overrightarrow {B'C} ) = {180^o} - {45^o} = {135^o}\)
Trả lời câu hỏi Thực hành 9 trang 50 SGK Toán 12 Chân trời sáng tạo
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng 1.
a) Tính các tích vô hướng: \(\overrightarrow {AB} .\overrightarrow {A'C'} \), \(\overrightarrow {AB} .\overrightarrow {CC'} \)
b) Tính góc \((\overrightarrow {AC} .\overrightarrow {AC'} )\) (kết quả làm tròn đến phút).
Phương pháp giải:
a) Công thức tính tích vô hướng của 2 vecto: \(\overrightarrow u .\overrightarrow v = |\overrightarrow u |.|\overrightarrow v |.\cos (\overrightarrow u ,\overrightarrow v )\)
b) Trong không gian, cho hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) đều khác vectơ không. Từ một điểm A bất kỳ, gọi B và C là hai điểm sao cho \(\overrightarrow {AB} = \overrightarrow u \) và \(\overrightarrow {AC} = \overrightarrow v \). Khi đó góc \(\widehat {BAC}\) được gọi là góc giữa hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \).
Lời giải chi tiết:
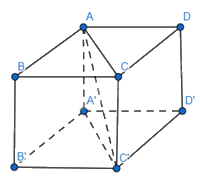
a) \(\overrightarrow {AB} .\overrightarrow {A'C'} = \overrightarrow {AB} .\overrightarrow {AC} = AB.AC.\cos \widehat {BAC} = 1.\sqrt 2 .\cos 45^\circ = 1\)
\(\overrightarrow {AB} .\overrightarrow {CC'} = \overrightarrow {AB} .\overrightarrow {BB'} = 0\) vì \(\overrightarrow {AB} \bot \overrightarrow {BB'} \)
b) Xét tam giác CAC’ vuông tại C:
\(AC = \sqrt 2 \); CC’ = 1 => \(\tan (\overrightarrow {AC} ,\overrightarrow {AC'} ) = \tan \widehat {C'AC} = \frac{{CC'}}{{AC}} = \frac{1}{{\sqrt 2 }} \Rightarrow \widehat {C'AC} = 35^\circ \).
Trả lời câu hỏi Vận dụng 4 trang 50 SGK Toán 12 Chân trời sáng tạo
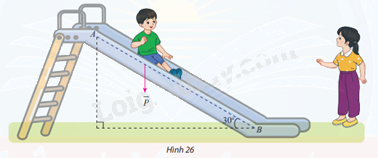
Một em nhỏ cân nặng m = 25 kg trượt trên cầu trượt dài 3,5m. Biết rằng, cầu trượt có góc nghiêng so với phương nằm ngang là \(30^\circ \) (Hình 26).
a) Tính độ lớn của trọng lực \(\overrightarrow P = m\overrightarrow g \) tác dụng lên em nhỏ, cho biết vectơ gia tốc rơi tự do \(\overrightarrow g \) có độ lớn 9,8\(m/{s^2}\)
b) Cho biết công A (J) sinh bởi một lực \(\overrightarrow F \) có độ dịch chuyển \(\overrightarrow d \) được tính bởi công thức \(A = \overrightarrow F .\overrightarrow d \). Hãy tính công sinh bởi trọng lực \(\overrightarrow P \) khi em nhỏ trượt hết chiều dài cầu trượt.
Phương pháp giải:
a) Áp dụng công thức tính trọng lực P = mg
b) Công thức tính công: \(A = Fs\cos \alpha \)
Lời giải chi tiết:
a) Độ lớn trọng lực tác dụng lên em nhỏ là: \(P = mg = 25.9,8 = 245N\)
b) Công sinh bởi trọng lực \(\overrightarrow P \) khi em nhỏ trượt hết chiều dài cầu trượt là: \(A = \overrightarrow F .\overrightarrow d = Pd\cos 60^\circ = 245.3,5.\frac{1}{2} = 428,75J\)
Trả lời câu hỏi Khám phá 5 trang 48 SGK Toán 12 Chân trời sáng tạo
a) Nhắc lại định nghĩa góc giữa hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) trong mặt phẳng.
b) Làm thế nào để định nghĩa góc giữa hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) trong không gian?
Phương pháp giải:
Nhớ lại định nghĩa đã học về góc giữa hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) trong mặt phẳng và suy luận ra góc giữa hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) trong không gian.
Lời giải chi tiết:
a) Trong mặt phẳng, cho hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) đều khác vectơ không. Từ một điểm A bất kỳ, gọi B và C là hai điểm sao cho \(\overrightarrow {AB} = \overrightarrow u \) và \(\overrightarrow {AC} = \overrightarrow v \). Khi đó góc \(\widehat {BAC}\) được gọi là góc giữa hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \).
b) Trong không gian, cho hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) đều khác vectơ không. Từ một điểm A bất kỳ, gọi B và C là hai điểm sao cho \(\overrightarrow {AB} = \overrightarrow u \) và \(\overrightarrow {AC} = \overrightarrow v \). Khi đó góc \(\widehat {BAC}\) được gọi là góc giữa hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \).
Trả lời câu hỏi Thực hành 8 trang 48 SGK Toán 12 Chân trời sáng tạo
Cho hình lập phương ABCD.A′B′C′D′. Xác định góc \((\overrightarrow {AC} ,\overrightarrow {B'D'} ),(\overrightarrow {A'A} ,\overrightarrow {CB'} )\)
Phương pháp giải:
Trong không gian, cho hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) đều khác vectơ không. Từ một điểm A bất kỳ, gọi B và C là hai điểm sao cho \(\overrightarrow {AB} = \overrightarrow u \) và \(\overrightarrow {AC} = \overrightarrow v \). Khi đó góc \(\widehat {BAC}\) được gọi là góc giữa hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \).
Lời giải chi tiết:
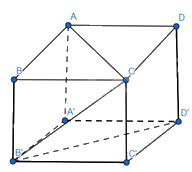
Góc \((\overrightarrow {AC} ,\overrightarrow {B'D'} )\) = góc \((\overrightarrow {AC} ,\overrightarrow {BD} )\) = \(90^\circ \) (góc giữa 2 đường chéo của hình vuông)
\((\overrightarrow {A'A} ,\overrightarrow {CB'} ) = (\overrightarrow {B'B} ,\overrightarrow {CB'} ) = {180^o} - (\overrightarrow {B'B} ,\overrightarrow {B'C} ) = {180^o} - {45^o} = {135^o}\)
Trả lời câu hỏi Khám phá 6 trang 49 SGK Toán 12 Chân trời sáng tạo
Trong không gian, cho \(\overrightarrow u \) và \(\overrightarrow v \) thoả mãn \(|\overrightarrow u | = 2\) , \(|\overrightarrow v | = 3\). Lấy một điểm A bất kì, gọi B và C là hai điểm sao cho \(\overrightarrow {AB} = \overrightarrow u \), \(\overrightarrow {AC} = \overrightarrow v \) (Hình 24). Giả sử \(\widehat {BAC} = 60^\circ \)
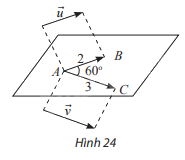
a) Tính góc \((\overrightarrow u ,\overrightarrow v )\)
b) Trong mặt phẳng (ABC), tính tích vô hướng \(\overrightarrow {AB} .\overrightarrow {AC} \)
Phương pháp giải:
a) Trong không gian, cho hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) đều khác vectơ không. Từ một điểm A bất kỳ, gọi B và C là hai điểm sao cho \(\overrightarrow {AB} = \overrightarrow u \) và \(\overrightarrow {AC} = \overrightarrow v \). Khi đó góc \(\widehat {BAC}\) được gọi là góc giữa hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \).
b) Công thức tính tích vô hướng của 2 vecto: \(\overrightarrow u .\overrightarrow v = |\overrightarrow u |.|\overrightarrow v |.\cos (\overrightarrow u ,\overrightarrow v )\)
Lời giải chi tiết:
a) Góc \((\overrightarrow u ,\overrightarrow v )\) = \(\widehat {BAC} = 60^\circ \)
b) \(\overrightarrow {AB} .\overrightarrow {AC} \) = \(AB.AC.\cos \widehat {BAC} = 2.3.\cos 60^\circ = 3\)
Trả lời câu hỏi Thực hành 9 trang 50 SGK Toán 12 Chân trời sáng tạo
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng 1.
a) Tính các tích vô hướng: \(\overrightarrow {AB} .\overrightarrow {A'C'} \), \(\overrightarrow {AB} .\overrightarrow {CC'} \)
b) Tính góc \((\overrightarrow {AC} .\overrightarrow {AC'} )\) (kết quả làm tròn đến phút).
Phương pháp giải:
a) Công thức tính tích vô hướng của 2 vecto: \(\overrightarrow u .\overrightarrow v = |\overrightarrow u |.|\overrightarrow v |.\cos (\overrightarrow u ,\overrightarrow v )\)
b) Trong không gian, cho hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) đều khác vectơ không. Từ một điểm A bất kỳ, gọi B và C là hai điểm sao cho \(\overrightarrow {AB} = \overrightarrow u \) và \(\overrightarrow {AC} = \overrightarrow v \). Khi đó góc \(\widehat {BAC}\) được gọi là góc giữa hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \).
Lời giải chi tiết:
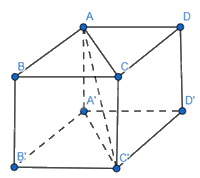
a) \(\overrightarrow {AB} .\overrightarrow {A'C'} = \overrightarrow {AB} .\overrightarrow {AC} = AB.AC.\cos \widehat {BAC} = 1.\sqrt 2 .\cos 45^\circ = 1\)
\(\overrightarrow {AB} .\overrightarrow {CC'} = \overrightarrow {AB} .\overrightarrow {BB'} = 0\) vì \(\overrightarrow {AB} \bot \overrightarrow {BB'} \)
b) Xét tam giác CAC’ vuông tại C:
\(AC = \sqrt 2 \); CC’ = 1 => \(\tan (\overrightarrow {AC} ,\overrightarrow {AC'} ) = \tan \widehat {C'AC} = \frac{{CC'}}{{AC}} = \frac{1}{{\sqrt 2 }} \Rightarrow \widehat {C'AC} = 35^\circ \).
Trả lời câu hỏi Vận dụng 4 trang 50 SGK Toán 12 Chân trời sáng tạo
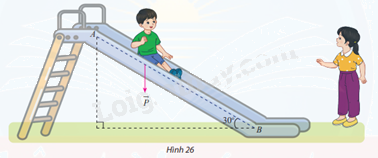
Một em nhỏ cân nặng m = 25 kg trượt trên cầu trượt dài 3,5m. Biết rằng, cầu trượt có góc nghiêng so với phương nằm ngang là \(30^\circ \) (Hình 26).
a) Tính độ lớn của trọng lực \(\overrightarrow P = m\overrightarrow g \) tác dụng lên em nhỏ, cho biết vectơ gia tốc rơi tự do \(\overrightarrow g \) có độ lớn 9,8\(m/{s^2}\)
b) Cho biết công A (J) sinh bởi một lực \(\overrightarrow F \) có độ dịch chuyển \(\overrightarrow d \) được tính bởi công thức \(A = \overrightarrow F .\overrightarrow d \). Hãy tính công sinh bởi trọng lực \(\overrightarrow P \) khi em nhỏ trượt hết chiều dài cầu trượt.
Phương pháp giải:
a) Áp dụng công thức tính trọng lực P = mg
b) Công thức tính công: \(A = Fs\cos \alpha \)
Lời giải chi tiết:
a) Độ lớn trọng lực tác dụng lên em nhỏ là: \(P = mg = 25.9,8 = 245N\)
b) Công sinh bởi trọng lực \(\overrightarrow P \) khi em nhỏ trượt hết chiều dài cầu trượt là: \(A = \overrightarrow F .\overrightarrow d = Pd\cos 60^\circ = 245.3,5.\frac{1}{2} = 428,75J\)
Mục 4 của SGK Toán 12 tập 1 chương trình Chân trời sáng tạo tập trung vào việc nghiên cứu về giới hạn của hàm số. Đây là một khái niệm nền tảng quan trọng trong giải tích, giúp học sinh hiểu rõ hơn về hành vi của hàm số khi biến số tiến tới một giá trị nhất định. Việc nắm vững kiến thức về giới hạn là bước đệm quan trọng để học sinh tiếp cận các khái niệm phức tạp hơn như đạo hàm và tích phân.
Các bài tập trong mục 4 SGK Toán 12 tập 1 Chân trời sáng tạo được chia thành nhiều dạng khác nhau, bao gồm:
Để giải bài tập này, ta có thể phân tích tử thức thành nhân tử:
(x^2 - 4) = (x - 2)(x + 2)
Khi đó, biểu thức trở thành:
lim (x->2) (x - 2)(x + 2) / (x - 2) = lim (x->2) (x + 2) = 2 + 2 = 4
Để giải bài tập này, ta chia cả tử và mẫu cho x:
lim (x->+∞) (2x + 1) / (x - 3) = lim (x->+∞) (2 + 1/x) / (1 - 3/x) = (2 + 0) / (1 - 0) = 2
Để tìm giới hạn của hàm số tại x = 1, ta cần tính giới hạn bên trái và giới hạn bên phải:
lim (x->1-) f(x) = lim (x->1-) x^2 = 1^2 = 1
lim (x->1+) f(x) = lim (x->1+) (2x - 1) = 2(1) - 1 = 1
Vì lim (x->1-) f(x) = lim (x->1+) f(x) = 1, nên lim (x->1) f(x) = 1
Kiến thức về giới hạn là nền tảng quan trọng để học sinh tiếp cận các khái niệm phức tạp hơn trong giải tích, như đạo hàm, tích phân, và các ứng dụng của chúng trong các lĩnh vực khoa học và kỹ thuật. Việc nắm vững kiến thức về giới hạn giúp học sinh hiểu rõ hơn về hành vi của hàm số, giải quyết các bài toán thực tế, và phát triển tư duy logic và khả năng phân tích.
Hy vọng rằng với lời giải chi tiết và hướng dẫn giải bài tập mục 4 trang 48,49,50 SGK Toán 12 tập 1 Chân trời sáng tạo, các em học sinh sẽ tự tin hơn trong việc học tập và đạt kết quả cao trong môn Toán.