Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 5 trang 32, 33, 34 SGK Toán 12 tập 1 chương trình Chân trời sáng tạo. Giaitoan.edu.vn cung cấp đáp án chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
Chúng tôi hiểu rằng việc học Toán đôi khi có thể gặp nhiều khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải chi tiết, kèm theo các bước giải cụ thể, giúp các em hiểu rõ bản chất của bài toán.
Vận dụng đạo hàm và khảo sát hàm số để giải quyết một số vấn đề liên quan đến thực tiễn
Trả lời câu hỏi Thực hành 5 trang 35 SGK Toán 12 Chân trời sáng tạo
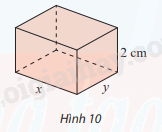
Người ta muốn chế tạo một chiếc hộp hình hộp chữ nhật có thể tích 500\(c{m^3}\) với yêu cầu dùng ít vật liệu nhất. Chiều cao hộp phải là 2 cm, các kích thước khác là x, y với x > 0 và y > 0.
a) Hãy biểu thị y theo x
b) Chứng tỏ rằng diện tích toàn phần của chiếc hộp là: \(S(x) = 500 + 4x + \frac{{1000}}{x}\)
c) Lập bảng biến thiên của hàm số S(x) trên khoảng (0; \( + \infty \)).
d) Kích thước của hộp là bao nhiêu thì dùng ít vật liệu nhất? (Làm tròn kết quả đến hàng phần mười.)
Phương pháp giải:
a) Dựa vào công thức thể tích hình hộp chữ nhật V = xyh, từ đó suy ra mối liên hệ giữa x và y
b) Diện tích toàn phần của hình hộp chữ nhật: \({S_{tp}} = 2h(x + y) + 2xy\)
c) Lập bảng biến thiên và tìm giá trị nhỏ nhất của \({S_{tp}}\) trên tập xác định
Lời giải chi tiết:
a) \(y = \frac{{500}}{{2x}} = \frac{{250}}{x}\)
b) Diện tích toàn phần của chiếc hộp là: \(S(x) = 2.2(x + y) + 2xy = 4(x + \frac{{250}}{x}) + 2.x.\frac{{250}}{x} = 500 + 4x + \frac{{1000}}{x}\)
c) Tập xác định: \(D = (0; + \infty )\)
\(S'(x) = 4 - \frac{{1000}}{{{x^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 5\sqrt {10} \\x = - 5\sqrt {10} (loai)\end{array} \right.\)
\(\mathop {\lim }\limits_{x \to + \infty } S(x) = \mathop {\lim }\limits_{x \to + \infty } (500 + 4x + \frac{{1000}}{x}) = + \infty ;\mathop {\lim }\limits_{x \to - \infty } S(x) = \mathop {\lim }\limits_{x \to - \infty } (500 + 4x + \frac{{1000}}{x}) = - \infty \)
\(\mathop {\lim }\limits_{x \to {0^ + }} S(x) = \mathop {\lim }\limits_{x \to {0^ + }} (500 + 4x + \frac{{1000}}{x}) = + \infty ;\mathop {\lim }\limits_{x \to {0^ - }} S(x) = \mathop {\lim }\limits_{x \to {0^ - }} (500 + 4x + \frac{{1000}}{x}) = - \infty \)
Bảng biến thiên: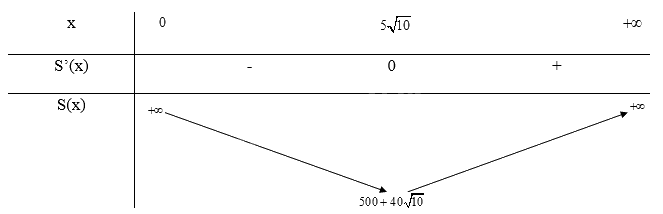
d) Để S(x) nhỏ nhất thì x = \(15,8\)(cm) và \(y = \frac{{250}}{x} = \frac{{250}}{{5\sqrt {10} }} \approx 15,8\)(cm)
Trả lời câu hỏi Thực hành 4 trang 35SGK Toán 12 Chân trời sáng tạo
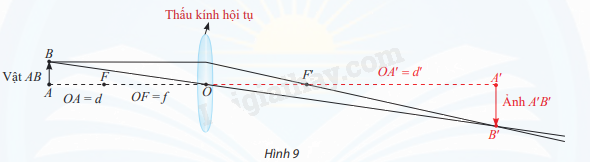
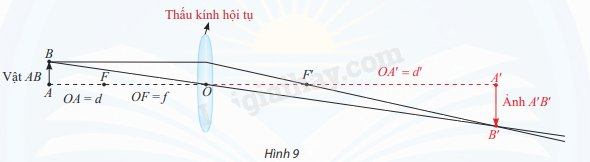
Xét một vật thật đặt trước thấu kính hội tụ có tiêu cự f > 0. Gọi d là khoảng cách từ vật đến thấu kính (d > 0), d’ là khoảng cách từ thấu kính đến ảnh (ảnh thật thì d’ > 0, ảnh ảo thì d’ < 0). Ta có công thức:
\(\frac{1}{f} = \frac{1}{d} + \frac{1}{{{d'}}}\) hay \(d' = \frac{{df}}{{d - f}}\)
(Vật lí 11, Nhà xuất bản Giáo dục Việt Nam, 2012, trang 182, 187)
Xét trường hợp f = 3, đặt x = d, y = d’. Ta có hàm số \(y = \frac{{3x}}{{x - 3}}\) và \(x \ne 3\).
a) Khảo sát và vẽ đồ thị của hàm số trên.
b) Dựa vào đồ thị hàm số trên, hãy cho biết vị trí của vật để ảnh của vật là: ảnh thật, ảnh ảo.
c) Khi vật tiến gần đến tiêu điểm thì ảnh thay đổi như thế nào?
Phương pháp giải:
a) Bước 1. Tìm tập xác định của hàm số
Bước 2. Xét sự biến thiên của hàm số
− Tìm đạo hàm y', xét dấu y', xác định khoảng đơn điệu, cực trị (nếu có) của hàm số.
− Tìm giới hạn tại vô cực, giới hạn vô cực của hàm số và các đường tiệm cận của đồ thị hàm số (nếu có).
− Lập bảng biến thiên của hàm số.
Bước 3. Vẽ đồ thị của hàm số
− Xác định các điểm cực trị (nếu có), giao điểm của đồ thị với các trục toạ độ
− Vẽ các đường tiệm cận của đồ thị hàm số (nếu có).
− Vẽ đồ thị hàm số.
b) Ảnh ảo nếu d’ < 0 và ảnh thật nếu d’ > 0
c) Tìm giới hạn của d’ khi d tiến dần đến f
Lời giải chi tiết:
a) \(y = \frac{{3x}}{{x - 3}}\)
Tập xác định: \(D = \mathbb{R}\backslash \{ 3\} \)
\(y' = \frac{{ - 9}}{{{{(x - 3)}^2}}} \le 0 \Leftrightarrow \forall x \in D\) nên hàm số nghịch biến trên \(D\)
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \frac{{3x}}{{x - 3}} = 3;\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } (\frac{{3x}}{{x - 3}}) = 3\) nên y = 3 là tiệm cận ngang của đồ thị hàm số
\(\mathop {\lim }\limits_{x \to {3^ + }} y = \mathop {\lim }\limits_{x \to {3^ + }} \frac{{3x}}{{x - 3}} = + \infty ;\mathop {\lim }\limits_{x \to {3^ - }} y = \mathop {\lim }\limits_{x \to {3^ - }} \frac{{3x}}{{x - 3}} = - \infty \) nên x = 3 là tiệm cận đứng của đồ thị hàm số
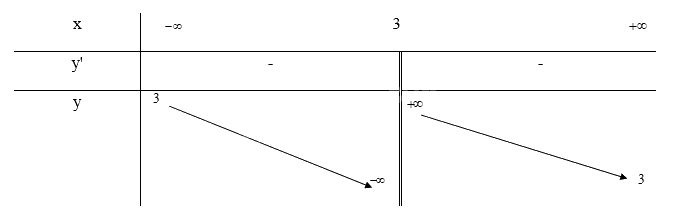
Khi x = 0 thì y = 0 nên (0;0) là giao điểm của y với trục Oy, Ox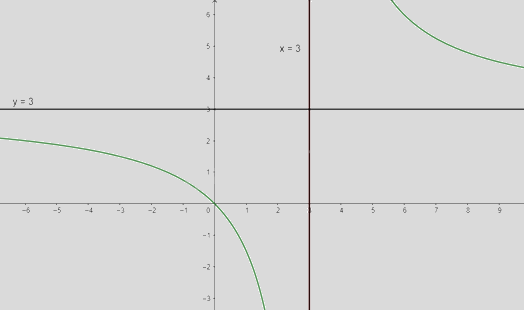
b) Để ảnh của vật là ảnh thật thì d’ > 0 hay y > 0 => x < 0 hoặc x > 3 hay d > 3 (do d là khoảng cách từ vật đến thấu kính nên d không thể nhỏ hơn 0)
Để ảnh của vật là ảnh ảo thì d’ < 0 hay y < 0 => 0 < x < 3 hay 0 < d < 3
c) Khi vật tiến gần đến tiêu điểm thì khoảng cách từ ảnh đến thấu kính tiến dần tới vô cùng, ảnh của vật dần biến thành ảnh ảo
Trả lời câu hỏi Thực hành 4 trang 35SGK Toán 12 Chân trời sáng tạo
Xét một vật thật đặt trước thấu kính hội tụ có tiêu cự f > 0. Gọi d là khoảng cách từ vật đến thấu kính (d > 0), d’ là khoảng cách từ thấu kính đến ảnh (ảnh thật thì d’ > 0, ảnh ảo thì d’ < 0). Ta có công thức:
\(\frac{1}{f} = \frac{1}{d} + \frac{1}{{{d'}}}\) hay \(d' = \frac{{df}}{{d - f}}\)
(Vật lí 11, Nhà xuất bản Giáo dục Việt Nam, 2012, trang 182, 187)
Xét trường hợp f = 3, đặt x = d, y = d’. Ta có hàm số \(y = \frac{{3x}}{{x - 3}}\) và \(x \ne 3\).
a) Khảo sát và vẽ đồ thị của hàm số trên.
b) Dựa vào đồ thị hàm số trên, hãy cho biết vị trí của vật để ảnh của vật là: ảnh thật, ảnh ảo.
c) Khi vật tiến gần đến tiêu điểm thì ảnh thay đổi như thế nào?
Phương pháp giải:
a) Bước 1. Tìm tập xác định của hàm số
Bước 2. Xét sự biến thiên của hàm số
− Tìm đạo hàm y', xét dấu y', xác định khoảng đơn điệu, cực trị (nếu có) của hàm số.
− Tìm giới hạn tại vô cực, giới hạn vô cực của hàm số và các đường tiệm cận của đồ thị hàm số (nếu có).
− Lập bảng biến thiên của hàm số.
Bước 3. Vẽ đồ thị của hàm số
− Xác định các điểm cực trị (nếu có), giao điểm của đồ thị với các trục toạ độ
− Vẽ các đường tiệm cận của đồ thị hàm số (nếu có).
− Vẽ đồ thị hàm số.
b) Ảnh ảo nếu d’ < 0 và ảnh thật nếu d’ > 0
c) Tìm giới hạn của d’ khi d tiến dần đến f
Lời giải chi tiết:
a) \(y = \frac{{3x}}{{x - 3}}\)
Tập xác định: \(D = \mathbb{R}\backslash \{ 3\} \)
\(y' = \frac{{ - 9}}{{{{(x - 3)}^2}}} \le 0 \Leftrightarrow \forall x \in D\) nên hàm số nghịch biến trên \(D\)
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \frac{{3x}}{{x - 3}} = 3;\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } (\frac{{3x}}{{x - 3}}) = 3\) nên y = 3 là tiệm cận ngang của đồ thị hàm số
\(\mathop {\lim }\limits_{x \to {3^ + }} y = \mathop {\lim }\limits_{x \to {3^ + }} \frac{{3x}}{{x - 3}} = + \infty ;\mathop {\lim }\limits_{x \to {3^ - }} y = \mathop {\lim }\limits_{x \to {3^ - }} \frac{{3x}}{{x - 3}} = - \infty \) nên x = 3 là tiệm cận đứng của đồ thị hàm số
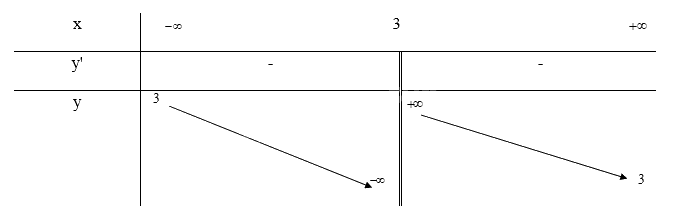
Khi x = 0 thì y = 0 nên (0;0) là giao điểm của y với trục Oy, Ox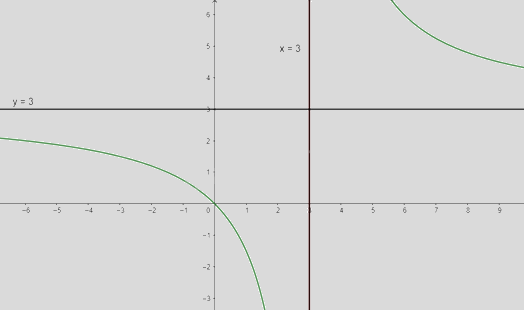
b) Để ảnh của vật là ảnh thật thì d’ > 0 hay y > 0 => x < 0 hoặc x > 3 hay d > 3 (do d là khoảng cách từ vật đến thấu kính nên d không thể nhỏ hơn 0)
Để ảnh của vật là ảnh ảo thì d’ < 0 hay y < 0 => 0 < x < 3 hay 0 < d < 3
c) Khi vật tiến gần đến tiêu điểm thì khoảng cách từ ảnh đến thấu kính tiến dần tới vô cùng, ảnh của vật dần biến thành ảnh ảo
Trả lời câu hỏi Thực hành 5 trang 35 SGK Toán 12 Chân trời sáng tạo
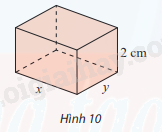
Người ta muốn chế tạo một chiếc hộp hình hộp chữ nhật có thể tích 500\(c{m^3}\) với yêu cầu dùng ít vật liệu nhất. Chiều cao hộp phải là 2 cm, các kích thước khác là x, y với x > 0 và y > 0.
a) Hãy biểu thị y theo x
b) Chứng tỏ rằng diện tích toàn phần của chiếc hộp là: \(S(x) = 500 + 4x + \frac{{1000}}{x}\)
c) Lập bảng biến thiên của hàm số S(x) trên khoảng (0; \( + \infty \)).
d) Kích thước của hộp là bao nhiêu thì dùng ít vật liệu nhất? (Làm tròn kết quả đến hàng phần mười.)
Phương pháp giải:
a) Dựa vào công thức thể tích hình hộp chữ nhật V = xyh, từ đó suy ra mối liên hệ giữa x và y
b) Diện tích toàn phần của hình hộp chữ nhật: \({S_{tp}} = 2h(x + y) + 2xy\)
c) Lập bảng biến thiên và tìm giá trị nhỏ nhất của \({S_{tp}}\) trên tập xác định
Lời giải chi tiết:
a) \(y = \frac{{500}}{{2x}} = \frac{{250}}{x}\)
b) Diện tích toàn phần của chiếc hộp là: \(S(x) = 2.2(x + y) + 2xy = 4(x + \frac{{250}}{x}) + 2.x.\frac{{250}}{x} = 500 + 4x + \frac{{1000}}{x}\)
c) Tập xác định: \(D = (0; + \infty )\)
\(S'(x) = 4 - \frac{{1000}}{{{x^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 5\sqrt {10} \\x = - 5\sqrt {10} (loai)\end{array} \right.\)
\(\mathop {\lim }\limits_{x \to + \infty } S(x) = \mathop {\lim }\limits_{x \to + \infty } (500 + 4x + \frac{{1000}}{x}) = + \infty ;\mathop {\lim }\limits_{x \to - \infty } S(x) = \mathop {\lim }\limits_{x \to - \infty } (500 + 4x + \frac{{1000}}{x}) = - \infty \)
\(\mathop {\lim }\limits_{x \to {0^ + }} S(x) = \mathop {\lim }\limits_{x \to {0^ + }} (500 + 4x + \frac{{1000}}{x}) = + \infty ;\mathop {\lim }\limits_{x \to {0^ - }} S(x) = \mathop {\lim }\limits_{x \to {0^ - }} (500 + 4x + \frac{{1000}}{x}) = - \infty \)
Bảng biến thiên: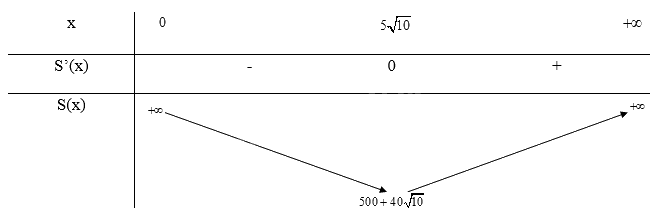
d) Để S(x) nhỏ nhất thì x = \(15,8\)(cm) và \(y = \frac{{250}}{x} = \frac{{250}}{{5\sqrt {10} }} \approx 15,8\)(cm)
Mục 5 của SGK Toán 12 tập 1 chương trình Chân trời sáng tạo tập trung vào việc nghiên cứu về đạo hàm của hàm số. Đây là một trong những kiến thức nền tảng quan trọng trong chương trình Toán học lớp 12, đóng vai trò then chốt trong việc giải quyết các bài toán liên quan đến cực trị, khoảng đơn điệu và ứng dụng của đạo hàm trong thực tế.
Trang 32 SGK Toán 12 tập 1 Chân trời sáng tạo thường chứa các bài tập áp dụng định nghĩa đạo hàm và quy tắc tính đạo hàm cơ bản. Các bài tập này giúp học sinh rèn luyện kỹ năng tính đạo hàm và làm quen với các dạng bài tập thường gặp.
Ví dụ: Tính đạo hàm của hàm số f(x) = x2 + 3x - 2.
Giải:
Trang 33 thường tập trung vào việc tính đạo hàm của các hàm số phức tạp hơn, đòi hỏi học sinh phải áp dụng linh hoạt các quy tắc tính đạo hàm và kết hợp các kiến thức đã học.
Ví dụ: Tính đạo hàm của hàm số f(x) = sin(x) * cos(x).
Giải:
Sử dụng quy tắc đạo hàm của tích: f'(x) = (sin(x))' * cos(x) + sin(x) * (cos(x))'
Ta có: (sin(x))' = cos(x) và (cos(x))' = -sin(x)
Vậy, f'(x) = cos(x) * cos(x) + sin(x) * (-sin(x)) = cos2(x) - sin2(x)
Trang 34 thường chứa các bài tập liên quan đến ứng dụng của đạo hàm để xét tính đơn điệu và cực trị của hàm số. Đây là những bài tập đòi hỏi học sinh phải hiểu sâu sắc về mối liên hệ giữa đạo hàm và tính chất của hàm số.
Ví dụ: Xét tính đơn điệu của hàm số f(x) = x3 - 3x2 + 2.
Giải:
Tính đạo hàm: f'(x) = 3x2 - 6x
Giải phương trình f'(x) = 0: 3x2 - 6x = 0 => x = 0 hoặc x = 2
Lập bảng xét dấu f'(x):
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| f'(x) | + | - | + | |
| f(x) | NB | Giảm | Tăng |
Kết luận: Hàm số f(x) đồng biến trên khoảng (-∞; 0) và (2; +∞), nghịch biến trên khoảng (0; 2).
Để học tốt môn Toán 12, đặc biệt là phần đạo hàm, các em cần:
Giaitoan.edu.vn hy vọng rằng với lời giải chi tiết và hướng dẫn cụ thể này, các em sẽ tự tin hơn trong việc giải các bài tập Toán 12 và đạt kết quả tốt nhất trong kỳ thi sắp tới.