Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 21, 22, 23 sách giáo khoa Toán 12 tập 2 chương trình Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong môn học.
Tính diện tích hình phẳng
Trả lời câu hỏi Thực hành 1 trang 22 SGK Toán 12 Chân trời sáng tạo
Tính diện tích hình phẳng giới hạn bởi đồ thị của hàm số \(y = 2x - {x^2}\), trục hoành và hai đường thẳng \(x = 0\), \(x = 3\).
Phương pháp giải:
Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành và các đường thẳng \(x = a\), \(x = b\) là \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} \).
Lời giải chi tiết:
Diện tích hình phẳng giới hạn bởi đồ thị của hàm số \(y = 2x - {x^2}\), trục hoành và hai đường thẳng \(x = 0\), \(x = 3\) là \(S = \int\limits_0^3 {\left| {2x - {x^2}} \right|dx} \)
Ta có \(2x - {x^2} = 0 \Leftrightarrow x = 0\) hoặc \(x = 2\).
Với \(x \in \left[ {0;2} \right]\) thì \(2x - {x^2} \ge 0\). Với \(x \in \left[ {2;3} \right]\) thì \(2x - {x^2} \le 0\).
Vậy \(S = \int\limits_0^3 {\left| {2x - {x^2}} \right|dx} = \int\limits_0^2 {\left( {2x - {x^2}} \right)dx} + \int\limits_2^3 {\left( {{x^2} - 2x} \right)dx} \)
\( = \left. {\left( {{x^2} - \frac{{{x^3}}}{3}} \right)} \right|_0^2 + \left. {\left( {\frac{{{x^3}}}{3} - {x^2}} \right)} \right|_2^3 = \left( {\frac{4}{3} - 0} \right) + \left[ {0 - \left( { - \frac{4}{3}} \right)} \right] = \frac{8}{3}\)
Trả lời câu hỏi Thực hành 2 trang 22 SGK Toán 12 Chân trời sáng tạo
Tính diện tích hình phẳng giới hạn bởi đồ thị của hàm số \(y = \cos x - 2\), trục hoành và hai đường thẳng \(x = 0\), \(x = \pi \).
Phương pháp giải:
Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành và các đường thẳng \(x = a\), \(x = b\) là \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} \).
Lời giải chi tiết:
Diện tích hình phẳng giới hạn bởi đồ thị của hàm số \(y = \cos x - 2\), trục hoành và hai đường thẳng \(x = 0\), \(x = \pi \) là \(S = \int\limits_0^\pi {\left| {\cos x - 2} \right|dx} \).
Do \(\cos x - 2 < 0\) với \(\forall x \in \left[ {0;\pi } \right]\).
Do đó \(S = \int\limits_0^\pi {\left( {2 - \cos x} \right)dx} = \left. {\left( {2x - \sin x} \right)} \right|_0^\pi = 2\pi - 0 = 2\pi \).
Trả lời câu hỏi Thực hành 3 trang 24 SGK Toán 12 Chân trời sáng tạo
Tính diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số \(y = {x^2} - 2x - 1\), \(y = x - 1\) và hai đường thẳng \(x = 1\), \(x = 4\).
Phương pháp giải:
Diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số \({f_1}\left( x \right)\) và \({f_2}\left( x \right)\) liên tục trên \(\left[ {a;b} \right]\) và hai đường thẳng \(x = a\), \(x = b\) là \(S = \int\limits_a^b {\left| {{f_1}\left( x \right) - {f_2}\left( x \right)} \right|dx} \)
Lời giải chi tiết:
Diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số \(y = {x^2} - 2x - 1\), \(y = x - 1\) và hai đường thẳng \(x = 1\), \(x = 4\) là:
\(S = \int\limits_1^4 {\left| {\left( {{x^2} - 2x - 1} \right) - \left( {x - 1} \right)} \right|dx} = \int\limits_1^4 {\left| {{x^2} - 3x} \right|dx} \)
Ta có \({x^2} - 3x = 0 \Leftrightarrow x = 0\) hoặc \(x = 3\)
Do đó
\(S = \int\limits_1^3 {\left| {{x^2} - 3x} \right|dx} + \int\limits_3^4 {\left| {{x^2} - 3x} \right|dx} = \left| {\int\limits_1^3 {\left( {{x^2} - 3x} \right)dx} } \right| + \left| {\int\limits_3^4 {\left( {{x^2} - 3x} \right)dx} } \right|\)
\( = \left| {\left. {\left( {\frac{{{x^3}}}{3} - 3\frac{{{x^2}}}{2}} \right)} \right|_1^3} \right| + \left| {\left. {\left( {\frac{{{x^3}}}{3} - 3\frac{{{x^2}}}{2}} \right)} \right|_3^4} \right| = \left| {\frac{{ - 9}}{2} - \frac{{ - 7}}{6}} \right| + \left| {\frac{{ - 8}}{3} - \frac{{ - 9}}{2}} \right| = \left| { - \frac{{10}}{3}} \right| + \left| {\frac{{11}}{6}} \right| = \frac{{31}}{6}\)
Trả lời câu hỏi Thực hành 4 trang 24 SGK Toán 12 Chân trời sáng tạo
Tính diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số \(y = 5x - {x^2}\), \(y = {x^2} - x\) và hai đường thẳng \(x = 0\), \(x = 2\).
Phương pháp giải:
Diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số \({f_1}\left( x \right)\) và \({f_2}\left( x \right)\) liên tục trên \(\left[ {a;b} \right]\) và hai đường thẳng \(x = a\), \(x = b\) là \(S = \int\limits_a^b {\left| {{f_1}\left( x \right) - {f_2}\left( x \right)} \right|dx} \)
Lời giải chi tiết:
Diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số \(y = 5x - {x^2}\), \(y = {x^2} - x\) và hai đường thẳng \(x = 0\), \(x = 2\) là
\(S = \int\limits_0^2 {\left| {\left( {5x - {x^2}} \right) - \left( {{x^2} - x} \right)} \right|dx} = \int\limits_0^2 {\left| {6x - 2{x^2}} \right|dx} = 2\int\limits_0^2 {\left| {{x^2} - 3x} \right|dx} \)
Ta có \({x^2} - 3x = 0 \Leftrightarrow x = 0\) hoặc \(x = 3\)
Do đó \(S = \left| {\int\limits_0^2 {\left( {{x^2} - 3x} \right)dx} } \right| = \left| {\left. {\left( {\frac{{{x^3}}}{3} - 3\frac{{{x^2}}}{2}} \right)} \right|_0^2} \right| = \left| { - \frac{{10}}{3}} \right| = \frac{{10}}{3}\)
Trả lời câu hỏi Khám phá 1 trang 21 SGK Toán 12 Chân trời sáng tạo
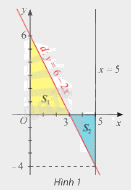
Gọi \(d\) là đồ thị của hàm số \(y = f\left( x \right) = 6 - 2x\). Kí hiệu \({S_1}\) là diện tích hình phẳng giới hạn bởi \(d\), trục hoành và trục tung; \({S_2}\) là diện tích hình phẳng giới hạn bởi \(d\), trục hoành và đường thẳng \(x = 5\) (Hình 1).
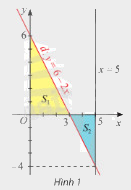
a) Tính \({S_1}\) và so sánh với \(\int\limits_0^3 {f\left( x \right)dx} \).
b) Tính \({S_2}\) và so sánh với \(\int\limits_3^5 {f\left( x \right)dx} \).
c) So sánh \(\int\limits_0^5 {\left| {f\left( x \right)} \right|dx} \) với \({S_1} + {S_2}\).
Phương pháp giải:
a) Theo hình vẽ, \({S_1}\) là diện tích tam giác \(OAB\). Tính diện tích tam giác \(OAB\), sau đó tính tích phân \(\int\limits_0^3 {f\left( x \right)dx} \) và so sánh các kết quả thu được.
b) Theo hình vẽ. \({S_2}\) là diện tích tam giác \(CBM\). Tính diện tích tam giác \(CBM\), sau đó tính tích phân \(\int\limits_3^5 {f\left( x \right)dx} \) và so sánh các kết quả thu được.
c) Tính \(\int\limits_0^5 {\left| {f\left( x \right)} \right|dx} = \int\limits_0^3 {\left| {f\left( x \right)} \right|dx} + \int\limits_3^5 {\left| {f\left( x \right)} \right|dx} \), sau đó phá dấu giá trị tuyệt đối và tính các tích phân cơ bản, sau đó so sánh kết quả thu được với \({S_1} + {S_2}\).
Lời giải chi tiết:
a) Tam giác \(OAB\) vuông tại \(O\), ta có \(OA = 6\), \(OB = 3\). Diện tích tam giác \(OAB\) là:
\({S_1} = \frac{{OA.OB}}{2} = \frac{{6.3}}{2} = 9\).
Ta có \(\int\limits_0^3 {f\left( x \right)dx} = \int\limits_0^3 {\left( {6 - 2x} \right)dx} = \left. {\left( {6x - {x^2}} \right)} \right|_0^3 = 9 - 0 = 9\).
Như vậy \({S_1} = \int\limits_0^3 {f\left( x \right)dx} \)
b) Tam giác \(CBM\) vuông tại \(M\), ta có \(MB = 2\), \(MC = 4\). Diện tích tam giác \(CBM\) là:
\({S_2} = \frac{{MB.MC}}{2} = \frac{{2.4}}{2} = 4\).
Ta có \(\int\limits_0^3 {f\left( x \right)dx} = \int\limits_3^5 {\left( {6 - 2x} \right)dx} = \left. {\left( {6x - {x^2}} \right)} \right|_3^5 = 5 - 9 = - 4\).
Như vậy \({S_2} = - \int\limits_3^5 {f\left( x \right)dx} \)
c) Ta có:
\(\int\limits_0^5 {\left| {f\left( x \right)} \right|dx} = \int\limits_0^5 {\left| {6 - 2x} \right|dx} = \int\limits_0^3 {\left| {6 - 2x} \right|dx} + \int\limits_3^5 {\left| {6 - 2x} \right|dx} = \int\limits_0^3 {\left( {6 - 2x} \right)dx} + \int\limits_3^5 {\left( {2x - 6} \right)dx} \)
\( = \left. {\left( {6x - {x^2}} \right)} \right|_0^3 + \left. {\left( {{x^2} - 6x} \right)} \right|_3^5 = \left( {9 - 0} \right) + \left[ {\left( { - 5} \right) - \left( { - 9} \right)} \right] = 13\)
Như vậy \(\int\limits_0^5 {\left| {f\left( x \right)} \right|dx} = 13 = {S_1} + {S_2}\).
Trả lời câu hỏi Khám phá 2 trang 23 SGK Toán 12 Chân trời sáng tạo
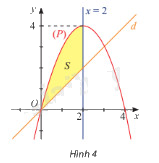
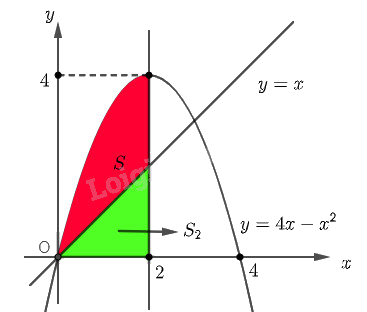
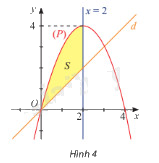
Cho hai hàm số \(y = 4x - {x^2}\) và \(y = x\) lần lượt có đồ thị \(\left( P \right)\) và \(d\) như hình 4.
a) Tính diện tích \({S_1}\) của hình phẳng giới hạn bởi \(\left( P \right)\), trục hoành và hai đường thẳng \(x = 0\), \(x = 2\).
b) Tính diện tích \(S\) của hình phẳng giới hạn bởi \(\left( P \right)\), \(d\) và hai đường thẳng \(x = 0\), \(x = 2\).
Phương pháp giải:
a) Diện tích \({S_1}\) của hình phẳng giới hạn bởi \(\left( P \right)\), trục hoành và hai đường thẳng \(x = 0\), \(x = 2\) là \({S_1} = \int\limits_0^2 {\left| {4x - {x^2}} \right|dx} \)
b) Diện tích \({S_2}\) của hình phẳng giới hạn bởi \(d\), trục hoành và hai đường thẳng \(x = 0\), \(x = 2\) là \({S_2} = \int\limits_0^2 {\left| x \right|dx} \).
Suy ra diện tích \(S\) của hình phẳng giới hạn bởi \(\left( P \right)\), \(d\) và hai đường thẳng \(x = 0\), \(x = 2\) là \(S = {S_1} - {S_2}\).
Lời giải chi tiết:
Diện tích \({S_1}\) của hình phẳng giới hạn bởi \(\left( P \right)\), trục hoành và hai đường thẳng \(x = 0\), \(x = 2\) là \({S_1} = \int\limits_0^2 {\left| {4x - {x^2}} \right|dx} \)
Ta thấy rằng với \(\forall x \in \left[ {0;2} \right]\) thì \(4x - {x^2} \ge 0\), do đó:
\({S_1} = \int\limits_0^2 {\left( {4x - {x^2}} \right)dx} = \left. {\left( {2{x^2} - \frac{{{x^3}}}{3}} \right)} \right|_0^2 = \frac{{16}}{3}\)
b) Diện tích \({S_2}\) của hình phẳng giới hạn bởi \(d\), trục hoành và hai đường thẳng \(x = 0\), \(x = 2\) là \({S_2} = \int\limits_0^2 {\left| x \right|dx} \).
Ta thấy rằng với \(\forall x \in \left[ {0;2} \right]\) thì \(x \ge 0\), do đó:
\({S_2} = \int\limits_0^2 {xdx} = \left. {\left( {\frac{{{x^2}}}{2}} \right)} \right|_0^2 = 2\)
Vậy diện tích \(S\) của hình phẳng giới hạn bởi \(\left( P \right)\), \(d\) và hai đường thẳng \(x = 0\), \(x = 2\) là \(S = {S_1} - {S_2} = \frac{{16}}{3} - 2 = \frac{{10}}{3}\).
Trả lời câu hỏi Vận dụng 1trang 24 SGK Toán 12 Chân trời sáng tạo
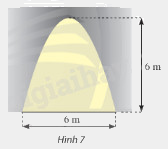
Mặt cắt của một cửa hầm có dạng là hình phẳng giới hạn bởi một parabol và đường thẳng nằm ngang như hình 7. Tính diện tích của cửa hầm.
Phương pháp giải:
Ta ghép mặt cắt của cửa hầm vào mặt phẳng \(Oxy\) như hình vẽ dưới đây.
Diện tích của cửa hầm chính là diện tích phần mặt phẳng giới hạn bởi parabol \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = 0\) và \(x = 6\).
Để tính được diện tích của cửa hầm, ta xác định phương trình của parabol \(y = f\left( x \right)\) như trong hình, sau đó tính tích phân \(S = \int\limits_0^6 {\left| {f\left( x \right)} \right|dx} \).
Lời giải chi tiết:
Ta ghép mặt cắt của cửa hầm vào mặt phẳng \(Oxy\) như hình vẽ dưới đây. Diện tích của cửa hầm chính là diện tích hình phẳng giới hạn bởi parabol \(y = f\left( x \right) = a{x^2} + bx + c\), trục hoành và hai đường thẳng \(x = 0\), \(x = 6\).
Ta nhận thấy rằng parabol đi qua các điểm có toạ độ \(\left( {0;0} \right)\), \(\left( {6;0} \right)\) và \(\left( {3;6} \right)\) (trục đối xứng của parabol đi qua đỉnh), do đó ta có hệ phương trình:
\(\left\{ {\begin{array}{*{20}{c}}{a{{.0}^2} + b.0 + c = 0}\\{a{{.6}^2} + b.6 + c = 0}\\{a{{.3}^2} + b.3 + c = 6}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{c = 0}\\{36a + 6b + c = 0}\\{9a + 3b + c = 6}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = - \frac{2}{3}}\\{b = 4}\\{c = 0}\end{array}} \right.} \right.\)
Vậy phương trình của parabol là \(y = - \frac{2}{3}{x^2} + 4x\).
Ta thấy rằng với \(x \in \left[ {0;6} \right]\) thì parabol nằm trên trục hoành. Do đó, diện tích của cửa hầm, cũng chính là diện tích hình phẳng giới hạn bởi parabol \(y = - \frac{2}{3}{x^2} + 4x\), trục hoành và các đường thẳng \(x = 0\), \(x = 6\) là:
\(S = \int\limits_0^6 {\left| { - \frac{2}{3}{x^2} + 4x} \right|dx} = \int\limits_0^6 {\left( { - \frac{2}{3}{x^2} + 4x} \right)dx} = \left. {\left( {\frac{{ - 2}}{9}{x^3} + 2{x^2}} \right)} \right|_0^6 = 24\)
Vậy diện tích của cửa hầm là 24 \({{\rm{m}}^2}\).
Trả lời câu hỏi Khám phá 1 trang 21 SGK Toán 12 Chân trời sáng tạo
Gọi \(d\) là đồ thị của hàm số \(y = f\left( x \right) = 6 - 2x\). Kí hiệu \({S_1}\) là diện tích hình phẳng giới hạn bởi \(d\), trục hoành và trục tung; \({S_2}\) là diện tích hình phẳng giới hạn bởi \(d\), trục hoành và đường thẳng \(x = 5\) (Hình 1).
a) Tính \({S_1}\) và so sánh với \(\int\limits_0^3 {f\left( x \right)dx} \).
b) Tính \({S_2}\) và so sánh với \(\int\limits_3^5 {f\left( x \right)dx} \).
c) So sánh \(\int\limits_0^5 {\left| {f\left( x \right)} \right|dx} \) với \({S_1} + {S_2}\).
Phương pháp giải:
a) Theo hình vẽ, \({S_1}\) là diện tích tam giác \(OAB\). Tính diện tích tam giác \(OAB\), sau đó tính tích phân \(\int\limits_0^3 {f\left( x \right)dx} \) và so sánh các kết quả thu được.
b) Theo hình vẽ. \({S_2}\) là diện tích tam giác \(CBM\). Tính diện tích tam giác \(CBM\), sau đó tính tích phân \(\int\limits_3^5 {f\left( x \right)dx} \) và so sánh các kết quả thu được.
c) Tính \(\int\limits_0^5 {\left| {f\left( x \right)} \right|dx} = \int\limits_0^3 {\left| {f\left( x \right)} \right|dx} + \int\limits_3^5 {\left| {f\left( x \right)} \right|dx} \), sau đó phá dấu giá trị tuyệt đối và tính các tích phân cơ bản, sau đó so sánh kết quả thu được với \({S_1} + {S_2}\).
Lời giải chi tiết:
a) Tam giác \(OAB\) vuông tại \(O\), ta có \(OA = 6\), \(OB = 3\). Diện tích tam giác \(OAB\) là:
\({S_1} = \frac{{OA.OB}}{2} = \frac{{6.3}}{2} = 9\).
Ta có \(\int\limits_0^3 {f\left( x \right)dx} = \int\limits_0^3 {\left( {6 - 2x} \right)dx} = \left. {\left( {6x - {x^2}} \right)} \right|_0^3 = 9 - 0 = 9\).
Như vậy \({S_1} = \int\limits_0^3 {f\left( x \right)dx} \)
b) Tam giác \(CBM\) vuông tại \(M\), ta có \(MB = 2\), \(MC = 4\). Diện tích tam giác \(CBM\) là:
\({S_2} = \frac{{MB.MC}}{2} = \frac{{2.4}}{2} = 4\).
Ta có \(\int\limits_0^3 {f\left( x \right)dx} = \int\limits_3^5 {\left( {6 - 2x} \right)dx} = \left. {\left( {6x - {x^2}} \right)} \right|_3^5 = 5 - 9 = - 4\).
Như vậy \({S_2} = - \int\limits_3^5 {f\left( x \right)dx} \)
c) Ta có:
\(\int\limits_0^5 {\left| {f\left( x \right)} \right|dx} = \int\limits_0^5 {\left| {6 - 2x} \right|dx} = \int\limits_0^3 {\left| {6 - 2x} \right|dx} + \int\limits_3^5 {\left| {6 - 2x} \right|dx} = \int\limits_0^3 {\left( {6 - 2x} \right)dx} + \int\limits_3^5 {\left( {2x - 6} \right)dx} \)
\( = \left. {\left( {6x - {x^2}} \right)} \right|_0^3 + \left. {\left( {{x^2} - 6x} \right)} \right|_3^5 = \left( {9 - 0} \right) + \left[ {\left( { - 5} \right) - \left( { - 9} \right)} \right] = 13\)
Như vậy \(\int\limits_0^5 {\left| {f\left( x \right)} \right|dx} = 13 = {S_1} + {S_2}\).
Trả lời câu hỏi Thực hành 1 trang 22 SGK Toán 12 Chân trời sáng tạo
Tính diện tích hình phẳng giới hạn bởi đồ thị của hàm số \(y = 2x - {x^2}\), trục hoành và hai đường thẳng \(x = 0\), \(x = 3\).
Phương pháp giải:
Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành và các đường thẳng \(x = a\), \(x = b\) là \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} \).
Lời giải chi tiết:
Diện tích hình phẳng giới hạn bởi đồ thị của hàm số \(y = 2x - {x^2}\), trục hoành và hai đường thẳng \(x = 0\), \(x = 3\) là \(S = \int\limits_0^3 {\left| {2x - {x^2}} \right|dx} \)
Ta có \(2x - {x^2} = 0 \Leftrightarrow x = 0\) hoặc \(x = 2\).
Với \(x \in \left[ {0;2} \right]\) thì \(2x - {x^2} \ge 0\). Với \(x \in \left[ {2;3} \right]\) thì \(2x - {x^2} \le 0\).
Vậy \(S = \int\limits_0^3 {\left| {2x - {x^2}} \right|dx} = \int\limits_0^2 {\left( {2x - {x^2}} \right)dx} + \int\limits_2^3 {\left( {{x^2} - 2x} \right)dx} \)
\( = \left. {\left( {{x^2} - \frac{{{x^3}}}{3}} \right)} \right|_0^2 + \left. {\left( {\frac{{{x^3}}}{3} - {x^2}} \right)} \right|_2^3 = \left( {\frac{4}{3} - 0} \right) + \left[ {0 - \left( { - \frac{4}{3}} \right)} \right] = \frac{8}{3}\)
Trả lời câu hỏi Thực hành 2 trang 22 SGK Toán 12 Chân trời sáng tạo
Tính diện tích hình phẳng giới hạn bởi đồ thị của hàm số \(y = \cos x - 2\), trục hoành và hai đường thẳng \(x = 0\), \(x = \pi \).
Phương pháp giải:
Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành và các đường thẳng \(x = a\), \(x = b\) là \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} \).
Lời giải chi tiết:
Diện tích hình phẳng giới hạn bởi đồ thị của hàm số \(y = \cos x - 2\), trục hoành và hai đường thẳng \(x = 0\), \(x = \pi \) là \(S = \int\limits_0^\pi {\left| {\cos x - 2} \right|dx} \).
Do \(\cos x - 2 < 0\) với \(\forall x \in \left[ {0;\pi } \right]\).
Do đó \(S = \int\limits_0^\pi {\left( {2 - \cos x} \right)dx} = \left. {\left( {2x - \sin x} \right)} \right|_0^\pi = 2\pi - 0 = 2\pi \).
Trả lời câu hỏi Khám phá 2 trang 23 SGK Toán 12 Chân trời sáng tạo
Cho hai hàm số \(y = 4x - {x^2}\) và \(y = x\) lần lượt có đồ thị \(\left( P \right)\) và \(d\) như hình 4.
a) Tính diện tích \({S_1}\) của hình phẳng giới hạn bởi \(\left( P \right)\), trục hoành và hai đường thẳng \(x = 0\), \(x = 2\).
b) Tính diện tích \(S\) của hình phẳng giới hạn bởi \(\left( P \right)\), \(d\) và hai đường thẳng \(x = 0\), \(x = 2\).
Phương pháp giải:
a) Diện tích \({S_1}\) của hình phẳng giới hạn bởi \(\left( P \right)\), trục hoành và hai đường thẳng \(x = 0\), \(x = 2\) là \({S_1} = \int\limits_0^2 {\left| {4x - {x^2}} \right|dx} \)
b) Diện tích \({S_2}\) của hình phẳng giới hạn bởi \(d\), trục hoành và hai đường thẳng \(x = 0\), \(x = 2\) là \({S_2} = \int\limits_0^2 {\left| x \right|dx} \).
Suy ra diện tích \(S\) của hình phẳng giới hạn bởi \(\left( P \right)\), \(d\) và hai đường thẳng \(x = 0\), \(x = 2\) là \(S = {S_1} - {S_2}\).
Lời giải chi tiết:
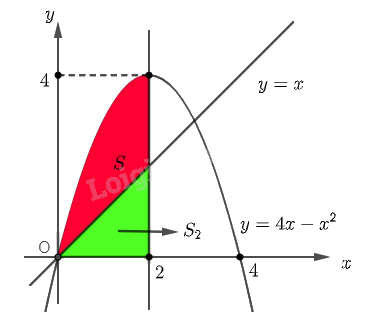
Diện tích \({S_1}\) của hình phẳng giới hạn bởi \(\left( P \right)\), trục hoành và hai đường thẳng \(x = 0\), \(x = 2\) là \({S_1} = \int\limits_0^2 {\left| {4x - {x^2}} \right|dx} \)
Ta thấy rằng với \(\forall x \in \left[ {0;2} \right]\) thì \(4x - {x^2} \ge 0\), do đó:
\({S_1} = \int\limits_0^2 {\left( {4x - {x^2}} \right)dx} = \left. {\left( {2{x^2} - \frac{{{x^3}}}{3}} \right)} \right|_0^2 = \frac{{16}}{3}\)
b) Diện tích \({S_2}\) của hình phẳng giới hạn bởi \(d\), trục hoành và hai đường thẳng \(x = 0\), \(x = 2\) là \({S_2} = \int\limits_0^2 {\left| x \right|dx} \).
Ta thấy rằng với \(\forall x \in \left[ {0;2} \right]\) thì \(x \ge 0\), do đó:
\({S_2} = \int\limits_0^2 {xdx} = \left. {\left( {\frac{{{x^2}}}{2}} \right)} \right|_0^2 = 2\)
Vậy diện tích \(S\) của hình phẳng giới hạn bởi \(\left( P \right)\), \(d\) và hai đường thẳng \(x = 0\), \(x = 2\) là \(S = {S_1} - {S_2} = \frac{{16}}{3} - 2 = \frac{{10}}{3}\).
Trả lời câu hỏi Thực hành 3 trang 24 SGK Toán 12 Chân trời sáng tạo
Tính diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số \(y = {x^2} - 2x - 1\), \(y = x - 1\) và hai đường thẳng \(x = 1\), \(x = 4\).
Phương pháp giải:
Diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số \({f_1}\left( x \right)\) và \({f_2}\left( x \right)\) liên tục trên \(\left[ {a;b} \right]\) và hai đường thẳng \(x = a\), \(x = b\) là \(S = \int\limits_a^b {\left| {{f_1}\left( x \right) - {f_2}\left( x \right)} \right|dx} \)
Lời giải chi tiết:
Diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số \(y = {x^2} - 2x - 1\), \(y = x - 1\) và hai đường thẳng \(x = 1\), \(x = 4\) là:
\(S = \int\limits_1^4 {\left| {\left( {{x^2} - 2x - 1} \right) - \left( {x - 1} \right)} \right|dx} = \int\limits_1^4 {\left| {{x^2} - 3x} \right|dx} \)
Ta có \({x^2} - 3x = 0 \Leftrightarrow x = 0\) hoặc \(x = 3\)
Do đó
\(S = \int\limits_1^3 {\left| {{x^2} - 3x} \right|dx} + \int\limits_3^4 {\left| {{x^2} - 3x} \right|dx} = \left| {\int\limits_1^3 {\left( {{x^2} - 3x} \right)dx} } \right| + \left| {\int\limits_3^4 {\left( {{x^2} - 3x} \right)dx} } \right|\)
\( = \left| {\left. {\left( {\frac{{{x^3}}}{3} - 3\frac{{{x^2}}}{2}} \right)} \right|_1^3} \right| + \left| {\left. {\left( {\frac{{{x^3}}}{3} - 3\frac{{{x^2}}}{2}} \right)} \right|_3^4} \right| = \left| {\frac{{ - 9}}{2} - \frac{{ - 7}}{6}} \right| + \left| {\frac{{ - 8}}{3} - \frac{{ - 9}}{2}} \right| = \left| { - \frac{{10}}{3}} \right| + \left| {\frac{{11}}{6}} \right| = \frac{{31}}{6}\)
Trả lời câu hỏi Thực hành 4 trang 24 SGK Toán 12 Chân trời sáng tạo
Tính diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số \(y = 5x - {x^2}\), \(y = {x^2} - x\) và hai đường thẳng \(x = 0\), \(x = 2\).
Phương pháp giải:
Diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số \({f_1}\left( x \right)\) và \({f_2}\left( x \right)\) liên tục trên \(\left[ {a;b} \right]\) và hai đường thẳng \(x = a\), \(x = b\) là \(S = \int\limits_a^b {\left| {{f_1}\left( x \right) - {f_2}\left( x \right)} \right|dx} \)
Lời giải chi tiết:
Diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số \(y = 5x - {x^2}\), \(y = {x^2} - x\) và hai đường thẳng \(x = 0\), \(x = 2\) là
\(S = \int\limits_0^2 {\left| {\left( {5x - {x^2}} \right) - \left( {{x^2} - x} \right)} \right|dx} = \int\limits_0^2 {\left| {6x - 2{x^2}} \right|dx} = 2\int\limits_0^2 {\left| {{x^2} - 3x} \right|dx} \)
Ta có \({x^2} - 3x = 0 \Leftrightarrow x = 0\) hoặc \(x = 3\)
Do đó \(S = \left| {\int\limits_0^2 {\left( {{x^2} - 3x} \right)dx} } \right| = \left| {\left. {\left( {\frac{{{x^3}}}{3} - 3\frac{{{x^2}}}{2}} \right)} \right|_0^2} \right| = \left| { - \frac{{10}}{3}} \right| = \frac{{10}}{3}\)
Trả lời câu hỏi Vận dụng 1trang 24 SGK Toán 12 Chân trời sáng tạo
Mặt cắt của một cửa hầm có dạng là hình phẳng giới hạn bởi một parabol và đường thẳng nằm ngang như hình 7. Tính diện tích của cửa hầm.
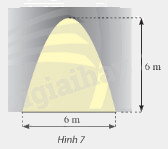
Phương pháp giải:
Ta ghép mặt cắt của cửa hầm vào mặt phẳng \(Oxy\) như hình vẽ dưới đây.
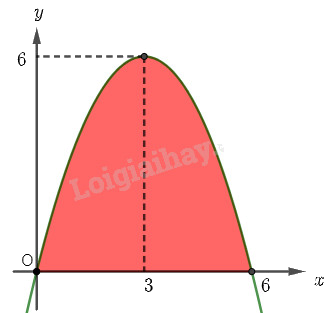
Diện tích của cửa hầm chính là diện tích phần mặt phẳng giới hạn bởi parabol \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = 0\) và \(x = 6\).
Để tính được diện tích của cửa hầm, ta xác định phương trình của parabol \(y = f\left( x \right)\) như trong hình, sau đó tính tích phân \(S = \int\limits_0^6 {\left| {f\left( x \right)} \right|dx} \).
Lời giải chi tiết:
Ta ghép mặt cắt của cửa hầm vào mặt phẳng \(Oxy\) như hình vẽ dưới đây. Diện tích của cửa hầm chính là diện tích hình phẳng giới hạn bởi parabol \(y = f\left( x \right) = a{x^2} + bx + c\), trục hoành và hai đường thẳng \(x = 0\), \(x = 6\).
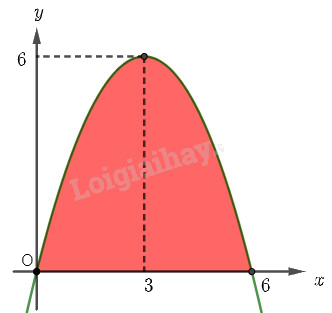
Ta nhận thấy rằng parabol đi qua các điểm có toạ độ \(\left( {0;0} \right)\), \(\left( {6;0} \right)\) và \(\left( {3;6} \right)\) (trục đối xứng của parabol đi qua đỉnh), do đó ta có hệ phương trình:
\(\left\{ {\begin{array}{*{20}{c}}{a{{.0}^2} + b.0 + c = 0}\\{a{{.6}^2} + b.6 + c = 0}\\{a{{.3}^2} + b.3 + c = 6}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{c = 0}\\{36a + 6b + c = 0}\\{9a + 3b + c = 6}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = - \frac{2}{3}}\\{b = 4}\\{c = 0}\end{array}} \right.} \right.\)
Vậy phương trình của parabol là \(y = - \frac{2}{3}{x^2} + 4x\).
Ta thấy rằng với \(x \in \left[ {0;6} \right]\) thì parabol nằm trên trục hoành. Do đó, diện tích của cửa hầm, cũng chính là diện tích hình phẳng giới hạn bởi parabol \(y = - \frac{2}{3}{x^2} + 4x\), trục hoành và các đường thẳng \(x = 0\), \(x = 6\) là:
\(S = \int\limits_0^6 {\left| { - \frac{2}{3}{x^2} + 4x} \right|dx} = \int\limits_0^6 {\left( { - \frac{2}{3}{x^2} + 4x} \right)dx} = \left. {\left( {\frac{{ - 2}}{9}{x^3} + 2{x^2}} \right)} \right|_0^6 = 24\)
Vậy diện tích của cửa hầm là 24 \({{\rm{m}}^2}\).
Mục 1 của chương trình Toán 12 tập 2 Chân trời sáng tạo thường tập trung vào một chủ đề quan trọng trong giải tích hoặc hình học. Để giải quyết các bài tập trong mục này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản, công thức và phương pháp giải liên quan.
Dưới đây là hướng dẫn giải chi tiết các bài tập trong mục 1 trang 21, 22, 23 SGK Toán 12 tập 2 Chân trời sáng tạo:
Đề bài: (Giả định đề bài cụ thể ở đây). Lời giải: (Giải chi tiết bài tập, bao gồm các bước thực hiện, giải thích rõ ràng và kết luận). Ví dụ, nếu bài tập yêu cầu tính đạo hàm của một hàm số, cần trình bày rõ các bước áp dụng quy tắc tính đạo hàm và kết quả cuối cùng.
Đề bài: (Giả định đề bài cụ thể ở đây). Lời giải: (Giải chi tiết bài tập, bao gồm các bước thực hiện, giải thích rõ ràng và kết luận). Nếu bài tập liên quan đến ứng dụng của đạo hàm để tìm cực trị, cần phân tích hàm số, tìm đạo hàm, giải phương trình đạo hàm bằng 0, và xác định các điểm cực trị.
Đề bài: (Giả định đề bài cụ thể ở đây). Lời giải: (Giải chi tiết bài tập, bao gồm các bước thực hiện, giải thích rõ ràng và kết luận). Nếu bài tập liên quan đến tích phân, cần xác định cận tích phân, chọn phương pháp tính tích phân phù hợp, và tính giá trị của tích phân.
Để củng cố kiến thức và rèn luyện kỹ năng giải toán, các em có thể tham khảo thêm các bài tập tương tự trong sách bài tập Toán 12 tập 2 Chân trời sáng tạo hoặc trên các trang web học toán online khác.
Hy vọng với hướng dẫn chi tiết này, các em sẽ tự tin giải quyết các bài tập trong mục 1 trang 21, 22, 23 SGK Toán 12 tập 2 Chân trời sáng tạo. Chúc các em học tập tốt!