Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài tập 6 trang 13 SGK Toán 12 tập 1 - Chân trời sáng tạo. Bài giải được trình bày rõ ràng, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các bài giải Toán 12, đáp ứng nhu cầu học tập của học sinh trên toàn quốc.
Xét một chất điểm chuyển động dọc theo trục (Ox). Toạ độ của chất điểm tại thời điểm (t) được xác định bởi hàm số (x(t) = {t^3} - 6{t^2} + 9t) với (t ge 0). Khi đó (x'(t)) là vận tốc của chất điểm tại thời điểm (t), kí hiệu (v(t)); (v'(t)) là gia tốc chuyển động của chất điểm tại thời điểm (t), kí hiệu (a(t)). a) Tìm các hàm (v(t))và (a(t)) b) Trong khoảng thời gian nào vận tốc của chất điểm tăng, trong khoảng thời gian nào vận tốc của chất điểm giảm?
Đề bài
Xét một chất điểm chuyển động dọc theo trục \(Ox\). Toạ độ của chất điểm tại thời điểm \(t\) được xác định bởi hàm số \(x(t) = {t^3} - 6{t^2} + 9t\) với \(t \ge 0\). Khi đó \(x'(t)\) là vận tốc của chất điểm tại thời điểm \(t\), kí hiệu \(v(t)\); \(v'(t)\) là gia tốc chuyển động của chất điểm tại thời điểm \(t\), kí hiệu \(a(t)\). a) Tìm các hàm \(v(t)\)và \(a(t)\)b) Trong khoảng thời gian nào vận tốc của chất điểm tăng, trong khoảng thời gian nào vận tốc của chất điểm giảm?
Phương pháp giải - Xem chi tiết
Áp dụng công thức tính đạo hàm, xét dấu đạo hàm
Lời giải chi tiết
a) \(v(t) = x'(t) = 3{t^2} - 12t + 9\)
\(a(t) = v'(t) = 6t - 12\)
b) Tập xác định: \(D = [0; + \infty ]\)
\(a(t) = 0 \Leftrightarrow t = 2\)
Bảng biến thiên:
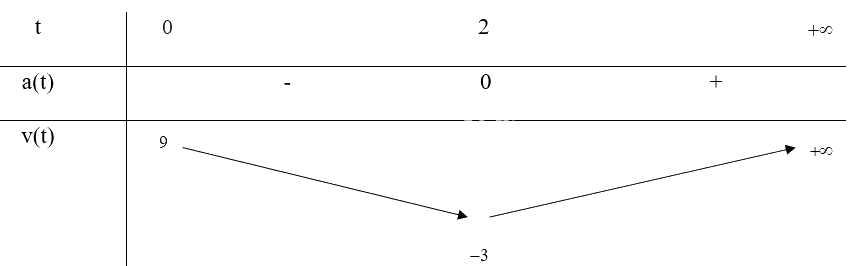
Vậy trong khoảng từ t = 0 đến t = 2 thì vận tốc của chất điểm giảm, từ t = 2 trở đi thì vận tốc của chất điểm tăng
Bài tập 6 trang 13 SGK Toán 12 tập 1 - Chân trời sáng tạo thuộc chương trình học về giới hạn của hàm số. Bài tập này yêu cầu học sinh vận dụng kiến thức về giới hạn một bên, giới hạn tại một điểm và các tính chất của giới hạn để giải quyết các bài toán cụ thể. Việc nắm vững kiến thức nền tảng và kỹ năng giải toán là yếu tố then chốt để hoàn thành tốt bài tập này.
Bài tập 6 bao gồm một số câu hỏi nhỏ, yêu cầu học sinh tính giới hạn của hàm số tại một điểm cho trước. Các hàm số có thể là hàm đa thức, hàm hữu tỉ, hoặc các hàm số khác. Để giải quyết bài tập này, học sinh cần:
Có nhiều phương pháp để giải bài tập về giới hạn, tùy thuộc vào dạng hàm số và yêu cầu của bài toán. Một số phương pháp phổ biến bao gồm:
Ví dụ: Tính limx→2 (x2 - 4) / (x - 2)
Giải:
Ta có: (x2 - 4) / (x - 2) = (x - 2)(x + 2) / (x - 2) = x + 2 (với x ≠ 2)
Do đó: limx→2 (x2 - 4) / (x - 2) = limx→2 (x + 2) = 2 + 2 = 4
Khi giải bài tập về giới hạn, học sinh cần lưu ý một số điểm sau:
Để củng cố kiến thức và kỹ năng giải bài tập về giới hạn, học sinh có thể tự giải các bài tập sau:
Bài tập 6 trang 13 SGK Toán 12 tập 1 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh hiểu sâu hơn về khái niệm giới hạn và các phương pháp tính giới hạn. Việc nắm vững kiến thức và kỹ năng giải bài tập này sẽ là nền tảng vững chắc cho việc học tập các chương trình Toán học nâng cao.