Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2, trang 16, 17 và 18 của sách giáo khoa Toán 12 tập 1, chương trình Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong các kỳ thi sắp tới.
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một đoạn
Trả lời câu hỏi Thực hành 3 trang 18 SGK Toán 12 Chân trời sáng tạo
Tam giác vuông có cạnh huyền bằng 5 cm có thể có diện tích lớn nhất bằng bao nhiêu?
Phương pháp giải:
Tìm hệ thức liên hệ giữa các cạnh, từ đó suy ra hàm số của diện tích tam giác vuông. Sau đó tìm đạo hàm, lập bảng biến thiên và xác định giá trị lớn nhất của hàm số
Lời giải chi tiết:
Đặt một cạnh góc vuông là x (x > 0) thì cạnh còn lại là \(\sqrt {25 - {x^2}} \)
Diện tích tam giác vuông là: \(f(x) = \frac{{1}}{2} x\sqrt {25 - {x^2}} \)
Tập xác định: \(D = (0; 5 )\)
\(f'(x) = \frac{{1}}{2}\sqrt {25 - {x^2}} - \frac{{1}}{2}. \frac{{{x^2}}}{{\sqrt {25 - {x^2}} }}\)
Tập xác định mới: \({D_1} = (0; 5 )\)
\(f'(x) = 0 \Leftrightarrow \left[ \begin{array}{l}x = \frac{{5\sqrt {2} }}{2}\\x = - \frac{{5\sqrt {2} }}{2}(loại)\end{array} \right.\)
Bảng biến thiên:
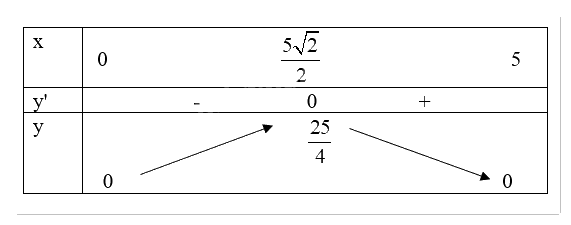
Từ bảng biến thiên, ta thấy \(\mathop {\max }\limits_D f(x) = f(\frac{{5\sqrt {2} }}{2}) = \frac{25}{4}\).
Vậy diện tích lớn nhất của tam giác là \(\frac{25}{4}\).
Trả lời câu hỏi Thực hành 2 trang 18 SGK Toán 12 Chân trời sáng tạo
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(g(x) = x + \frac{4}{{{x^2}}}\) trên đoạn [1;4]
Phương pháp giải:
Tìm đạo hàm g’(x), lập bảng biến thiên và xác định giá trị lớn nhất, giá trị nhỏ nhất của hàm số
Lời giải chi tiết:
Xét \(g(x) = x + \frac{4}{{{x^2}}}\) trên đoạn [1;4]
\(g'(x) = 1 - \frac{8}{{{x^3}}} = 0 \Leftrightarrow x = 2\)
Bảng biến thiên:
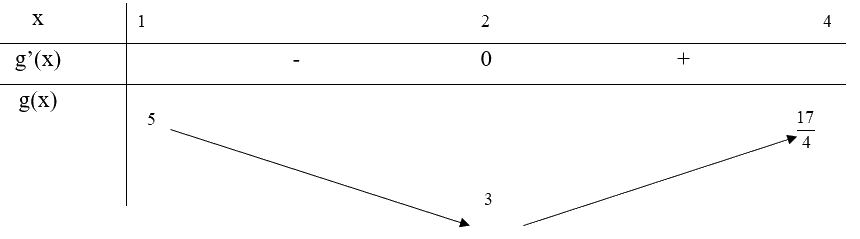
Từ bảng biến thiên, ta thấy \(\mathop {\min }\limits_{[1;4]} g(x) = g(2) = 3\) và \(\mathop {\max }\limits_{[1;4]} g(x) = g(1) = 5\)
Trả lời câu hỏi Khám phá 2 trang 16 SGK Toán 12 Chân trời sáng tạo
Hình 3 cho ta đồ thị của ba hàm số
\(f(x) = \frac{1}{2}{x^2}\); \(g(x) = \left\{ \begin{array}{l}\frac{1}{2}{x^2}\;\;\;\;\;\;\;\;\;\;\;neu\;x \le 2\;\\ - 4x + 10\;\;\;\;neu\;x \ge 2\end{array} \right.\) và \(h(x) = 3 - \frac{1}{2}{x^2}\) trên đoạn [-1;3]
a) Hàm số nào đạt giá trị lớn nhất tại một điểm cực đại của nó?
b) Các hàm số còn lại đạt giá trị lớn nhất tại điểm nào?
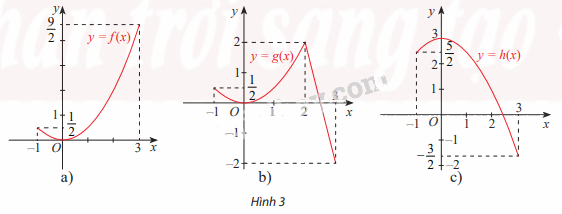
Phương pháp giải:
Quan sát đồ thị và chỉ ra điểm cực đại và giá trị lớn nhất của 3 hàm số.
Lời giải chi tiết:
a) \(h(x)\)đạt giá trị cực đại tại x = 0 và \(\mathop {\max h(x)}\limits_{[ - 1;3]} = h(0) = 3\)
b) \(\mathop {\max f(x)}\limits_{[ - 1;3]} = f(3) = \frac{9}{2}\) và \(\mathop {\max g(x)}\limits_{[ - 1;3]} = g(2) = 2\)
Trả lời câu hỏi Khám phá 2 trang 16 SGK Toán 12 Chân trời sáng tạo
Hình 3 cho ta đồ thị của ba hàm số
\(f(x) = \frac{1}{2}{x^2}\); \(g(x) = \left\{ \begin{array}{l}\frac{1}{2}{x^2}\;\;\;\;\;\;\;\;\;\;\;neu\;x \le 2\;\\ - 4x + 10\;\;\;\;neu\;x \ge 2\end{array} \right.\) và \(h(x) = 3 - \frac{1}{2}{x^2}\) trên đoạn [-1;3]
a) Hàm số nào đạt giá trị lớn nhất tại một điểm cực đại của nó?
b) Các hàm số còn lại đạt giá trị lớn nhất tại điểm nào?
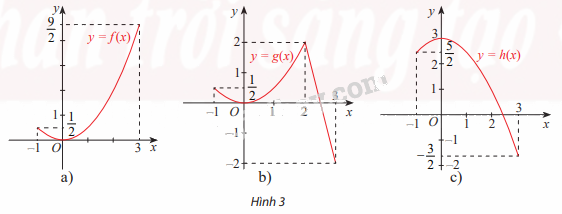
Phương pháp giải:
Quan sát đồ thị và chỉ ra điểm cực đại và giá trị lớn nhất của 3 hàm số.
Lời giải chi tiết:
a) \(h(x)\)đạt giá trị cực đại tại x = 0 và \(\mathop {\max h(x)}\limits_{[ - 1;3]} = h(0) = 3\)
b) \(\mathop {\max f(x)}\limits_{[ - 1;3]} = f(3) = \frac{9}{2}\) và \(\mathop {\max g(x)}\limits_{[ - 1;3]} = g(2) = 2\)
Trả lời câu hỏi Thực hành 2 trang 18 SGK Toán 12 Chân trời sáng tạo
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(g(x) = x + \frac{4}{{{x^2}}}\) trên đoạn [1;4]
Phương pháp giải:
Tìm đạo hàm g’(x), lập bảng biến thiên và xác định giá trị lớn nhất, giá trị nhỏ nhất của hàm số
Lời giải chi tiết:
Xét \(g(x) = x + \frac{4}{{{x^2}}}\) trên đoạn [1;4]
\(g'(x) = 1 - \frac{8}{{{x^3}}} = 0 \Leftrightarrow x = 2\)
Bảng biến thiên:
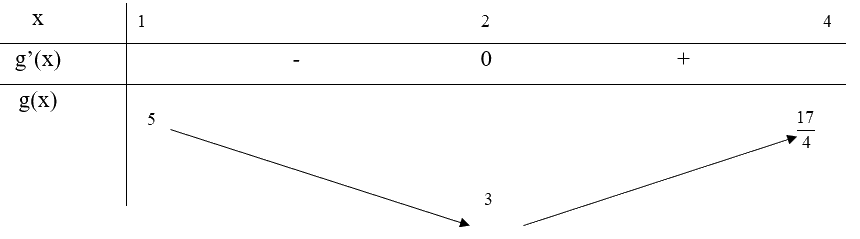
Từ bảng biến thiên, ta thấy \(\mathop {\min }\limits_{[1;4]} g(x) = g(2) = 3\) và \(\mathop {\max }\limits_{[1;4]} g(x) = g(1) = 5\)
Trả lời câu hỏi Thực hành 3 trang 18 SGK Toán 12 Chân trời sáng tạo
Tam giác vuông có cạnh huyền bằng 5 cm có thể có diện tích lớn nhất bằng bao nhiêu?
Phương pháp giải:
Tìm hệ thức liên hệ giữa các cạnh, từ đó suy ra hàm số của diện tích tam giác vuông. Sau đó tìm đạo hàm, lập bảng biến thiên và xác định giá trị lớn nhất của hàm số
Lời giải chi tiết:
Đặt một cạnh góc vuông là x (x > 0) thì cạnh còn lại là \(\sqrt {25 - {x^2}} \)
Diện tích tam giác vuông là: \(f(x) = \frac{{1}}{2} x\sqrt {25 - {x^2}} \)
Tập xác định: \(D = (0; 5 )\)
\(f'(x) = \frac{{1}}{2}\sqrt {25 - {x^2}} - \frac{{1}}{2}. \frac{{{x^2}}}{{\sqrt {25 - {x^2}} }}\)
Tập xác định mới: \({D_1} = (0; 5 )\)
\(f'(x) = 0 \Leftrightarrow \left[ \begin{array}{l}x = \frac{{5\sqrt {2} }}{2}\\x = - \frac{{5\sqrt {2} }}{2}(loại)\end{array} \right.\)
Bảng biến thiên:
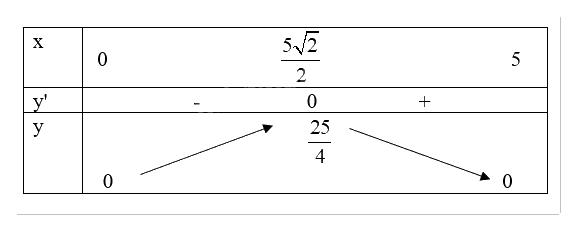
Từ bảng biến thiên, ta thấy \(\mathop {\max }\limits_D f(x) = f(\frac{{5\sqrt {2} }}{2}) = \frac{25}{4}\).
Vậy diện tích lớn nhất của tam giác là \(\frac{25}{4}\).
Mục 2 của SGK Toán 12 tập 1 chương trình Chân trời sáng tạo tập trung vào các kiến thức về giới hạn của hàm số. Đây là một trong những chủ đề quan trọng, nền tảng cho việc học tập các kiến thức nâng cao hơn trong chương trình Toán học. Việc hiểu rõ khái niệm giới hạn, các tính chất và các phương pháp tính giới hạn là vô cùng cần thiết.
Giới hạn của hàm số tại một điểm là giá trị mà hàm số tiến tới khi biến số x tiến tới điểm đó. Để hiểu rõ hơn, ta cần phân biệt giới hạn một bên và giới hạn hai bên. Giới hạn một bên xét khi x tiến tới điểm đó từ bên trái hoặc bên phải. Giới hạn hai bên chỉ tồn tại khi cả hai giới hạn một bên đều tồn tại và bằng nhau.
Giới hạn của một tổng, hiệu, tích, thương của các hàm số bằng tổng, hiệu, tích, thương của các giới hạn tương ứng (với điều kiện các giới hạn đều tồn tại và mẫu số khác 0). Ngoài ra, giới hạn của một hàm số lũy thừa bằng lũy thừa của giới hạn. Việc nắm vững các tính chất này giúp đơn giản hóa quá trình tính giới hạn.
Có nhiều phương pháp để tính giới hạn, tùy thuộc vào dạng của hàm số. Một số phương pháp phổ biến bao gồm:
Bài 1: Tính giới hạn lim (2x + 1) khi x -> 2.
Lời giải: Ta có thể thay trực tiếp x = 2 vào hàm số: lim (2x + 1) = 2*2 + 1 = 5.
Bài 2: Tính giới hạn lim (x^2 - 1) / (x - 1) khi x -> 1.
Lời giải: Ta phân tích tử số thành nhân tử: x^2 - 1 = (x - 1)(x + 1). Vậy lim (x^2 - 1) / (x - 1) = lim (x + 1) = 1 + 1 = 2.
Bài 3: Tính giới hạn lim (√(x + 1) - 1) / x khi x -> 0.
Lời giải: Ta nhân cả tử số và mẫu số với liên hợp của tử số: lim (√(x + 1) - 1) / x = lim ((√(x + 1) - 1)(√(x + 1) + 1)) / (x(√(x + 1) + 1)) = lim (x) / (x(√(x + 1) + 1)) = lim 1 / (√(x + 1) + 1) = 1 / (√(0 + 1) + 1) = 1/2.
Để nắm vững kiến thức về giới hạn, các em nên luyện tập thêm nhiều bài tập khác nhau. Các em có thể tìm thấy các bài tập trong SGK, sách bài tập hoặc trên các trang web học toán online như giaitoan.edu.vn. Việc giải bài tập thường xuyên sẽ giúp các em hiểu sâu hơn về lý thuyết và rèn luyện kỹ năng giải toán.
Khi giải bài tập về giới hạn, các em cần lưu ý một số điểm sau:
Hy vọng với những kiến thức và phương pháp giải bài tập được trình bày ở trên, các em sẽ tự tin hơn khi học tập và giải quyết các bài toán về giới hạn trong chương trình Toán 12 tập 1 Chân trời sáng tạo. Chúc các em học tốt!