Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác các bài tập Toán 12 tập 1 - Chân trời sáng tạo. Mục 2 trang 21 là một phần quan trọng trong chương trình học, đòi hỏi học sinh nắm vững kiến thức và kỹ năng giải quyết vấn đề.
Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải dễ hiểu, kèm theo các bước giải chi tiết, giúp bạn hiểu sâu sắc kiến thức và tự tin hơn trong quá trình học tập.
Đường tiệm cận ngang
Trả lời câu hỏi Thực hành 2 trang 21 SGK Toán 12 Chân trời sáng tạo
Tìm tiệm cận ngang của đồ thị các hàm số sau:
a) \(f(x) = \frac{{x - 1}}{{4x + 1}}\)
b) \(g(x) = \frac{{\sqrt x }}{{\sqrt x + 2}}\)
Phương pháp giải:
Đường thẳng y = m được gọi là một đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số y = f(x) nếu \(\mathop {\lim }\limits_{x \to - \infty } f(x) = m\) hoặc \(\mathop {\lim }\limits_{x \to + \infty } f(x) = m\)
Lời giải chi tiết:
a) Xét \(f(x) = \frac{{x - 1}}{{4x + 1}}\)
Tập xác định: \(D = \mathbb{R}\backslash \left\{ { - \frac{1}{4}} \right\}\)
Ta có: \(\mathop {\lim }\limits_{x \to + \infty } f(x) = \mathop {\lim }\limits_{x \to + \infty } \frac{{x - 1}}{{4x + 1}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{1 - \frac{1}{x}}}{{4 + \frac{1}{x}}} = \frac{1}{4}\); \(\mathop {\lim }\limits_{x \to - \infty } f(x) = \mathop {\lim }\limits_{x \to - \infty } \frac{{x - 1}}{{4x + 1}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{1 - \frac{1}{x}}}{{4 + \frac{1}{x}}} = \frac{1}{4}\)
Vậy đường thẳng \(y = \frac{1}{4}\) là tiệm cận ngang của đồ thị hàm số
b) Xét \(g(x) = \frac{{\sqrt x }}{{\sqrt x + 2}}\)
Tập xác định: \(D = [0; + \infty )\)
Ta có: \(\mathop {\lim }\limits_{x \to + \infty } g(x) = \mathop {\lim }\limits_{x \to + \infty } \frac{{\sqrt x }}{{\sqrt x + 2}} = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{{1 + \frac{2}{{\sqrt x }}}} = 1\)
Vậy đường thẳng \(y = 1\) là tiệm cận ngang của đồ thị hàm số
Trả lời câu hỏi Khám phá 2 trang 21 SGK Toán 12 Chân trời sáng tạo
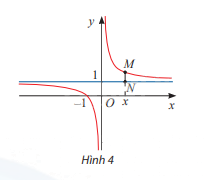
Cho hàm số \(y = \frac{{x + 1}}{x}\) có đồ thị như Hình 4.
a) Tìm \(\mathop {\lim }\limits_{x \to + \infty } = \frac{{x + 1}}{x},\mathop {\lim }\limits_{x \to - \infty } = \frac{{x + 1}}{x}\)
b) Đường thẳng vuông góc với trục Ox tại điểm x cắt đồ thị hàm số tại điểm M và cắt đường thẳng y = 1 tại điểm N (Hình 4). Tính MN theo x và nhận xét về MN khi \(x \to + \infty \) hoặc \(x \to - \infty \)
Phương pháp giải:
Quan sát đồ thị
Lời giải chi tiết:
a) Từ đồ thị ta thấy:
Khi \(x \to + \infty \)thì y tiến dần đến \(1\), vậy \(\mathop {\lim }\limits_{x \to + \infty } = \frac{{x + 1}}{x} = 1\)
Khi \(x \to - \infty \)thì y tiến dần đến \(1\), vậy \(\mathop {\lim }\limits_{x \to - \infty } = \frac{{x + 1}}{x} = 1\)
b) MN = y – 1 = \(\frac{{x + 1}}{x} - 1 = \frac{1}{x}\)
Khi \(x \to + \infty \) hoặc \(x \to - \infty \) thì MN tiến dần về 0
Trả lời câu hỏi Thực hành 2 trang 21 SGK Toán 12 Chân trời sáng tạo
Tìm tiệm cận ngang của đồ thị các hàm số sau:
a) \(f(x) = \frac{{x - 1}}{{4x + 1}}\)
b) \(g(x) = \frac{{\sqrt x }}{{\sqrt x + 2}}\)
Phương pháp giải:
Đường thẳng y = m được gọi là một đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số y = f(x) nếu \(\mathop {\lim }\limits_{x \to - \infty } f(x) = m\) hoặc \(\mathop {\lim }\limits_{x \to + \infty } f(x) = m\)
Lời giải chi tiết:
a) Xét \(f(x) = \frac{{x - 1}}{{4x + 1}}\)
Tập xác định: \(D = \mathbb{R}\backslash \left\{ { - \frac{1}{4}} \right\}\)
Ta có: \(\mathop {\lim }\limits_{x \to + \infty } f(x) = \mathop {\lim }\limits_{x \to + \infty } \frac{{x - 1}}{{4x + 1}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{1 - \frac{1}{x}}}{{4 + \frac{1}{x}}} = \frac{1}{4}\); \(\mathop {\lim }\limits_{x \to - \infty } f(x) = \mathop {\lim }\limits_{x \to - \infty } \frac{{x - 1}}{{4x + 1}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{1 - \frac{1}{x}}}{{4 + \frac{1}{x}}} = \frac{1}{4}\)
Vậy đường thẳng \(y = \frac{1}{4}\) là tiệm cận ngang của đồ thị hàm số
b) Xét \(g(x) = \frac{{\sqrt x }}{{\sqrt x + 2}}\)
Tập xác định: \(D = [0; + \infty )\)
Ta có: \(\mathop {\lim }\limits_{x \to + \infty } g(x) = \mathop {\lim }\limits_{x \to + \infty } \frac{{\sqrt x }}{{\sqrt x + 2}} = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{{1 + \frac{2}{{\sqrt x }}}} = 1\)
Vậy đường thẳng \(y = 1\) là tiệm cận ngang của đồ thị hàm số
Trả lời câu hỏi Khám phá 2 trang 21 SGK Toán 12 Chân trời sáng tạo
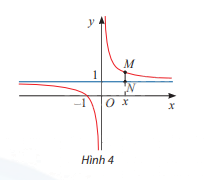
Cho hàm số \(y = \frac{{x + 1}}{x}\) có đồ thị như Hình 4.
a) Tìm \(\mathop {\lim }\limits_{x \to + \infty } = \frac{{x + 1}}{x},\mathop {\lim }\limits_{x \to - \infty } = \frac{{x + 1}}{x}\)
b) Đường thẳng vuông góc với trục Ox tại điểm x cắt đồ thị hàm số tại điểm M và cắt đường thẳng y = 1 tại điểm N (Hình 4). Tính MN theo x và nhận xét về MN khi \(x \to + \infty \) hoặc \(x \to - \infty \)
Phương pháp giải:
Quan sát đồ thị
Lời giải chi tiết:
a) Từ đồ thị ta thấy:
Khi \(x \to + \infty \)thì y tiến dần đến \(1\), vậy \(\mathop {\lim }\limits_{x \to + \infty } = \frac{{x + 1}}{x} = 1\)
Khi \(x \to - \infty \)thì y tiến dần đến \(1\), vậy \(\mathop {\lim }\limits_{x \to - \infty } = \frac{{x + 1}}{x} = 1\)
b) MN = y – 1 = \(\frac{{x + 1}}{x} - 1 = \frac{1}{x}\)
Khi \(x \to + \infty \) hoặc \(x \to - \infty \) thì MN tiến dần về 0
Mục 2 trang 21 SGK Toán 12 tập 1 - Chân trời sáng tạo thường tập trung vào các bài toán liên quan đến giới hạn của hàm số. Đây là một khái niệm nền tảng trong giải tích, đóng vai trò quan trọng trong việc hiểu các khái niệm phức tạp hơn như đạo hàm và tích phân. Để giải tốt các bài toán trong mục này, học sinh cần nắm vững định nghĩa giới hạn, các tính chất của giới hạn và các phương pháp tính giới hạn thường gặp.
Giới hạn của hàm số f(x) khi x tiến tới a được ký hiệu là limx→a f(x). Định nghĩa giới hạn cho biết giá trị mà hàm số f(x) tiến tới khi x tiến gần a, nhưng không nhất thiết phải bằng a.
Bài tập: Tính limx→2 (x2 - 4) / (x - 2)
Lời giải:
Ta có thể phân tích thành nhân tử biểu thức x2 - 4 như sau: x2 - 4 = (x - 2)(x + 2)
Do đó, limx→2 (x2 - 4) / (x - 2) = limx→2 [(x - 2)(x + 2)] / (x - 2) = limx→2 (x + 2) = 2 + 2 = 4
Để nắm vững kiến thức và kỹ năng giải các bài toán về giới hạn, bạn nên luyện tập thường xuyên với các bài tập trong SGK và các tài liệu tham khảo khác. Hãy chú trọng vào việc hiểu bản chất của các khái niệm và phương pháp giải, thay vì chỉ học thuộc lòng công thức.
| Dạng bài tập | Phương pháp giải |
|---|---|
| Tính giới hạn của hàm số đa thức | Thay trực tiếp giá trị x = a vào hàm số |
| Tính giới hạn của hàm số hữu tỉ | Phân tích thành nhân tử, nhân liên hợp, chia đa thức |
| Tính giới hạn của hàm số lượng giác | Sử dụng giới hạn đặc biệt, biến đổi lượng giác |
Giaitoan.edu.vn hy vọng rằng với lời giải chi tiết và hướng dẫn cụ thể này, bạn sẽ tự tin hơn trong việc giải các bài tập mục 2 trang 21 SGK Toán 12 tập 1 - Chân trời sáng tạo. Chúc bạn học tập tốt!