Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập Toán 12 tập 1 - Chân trời sáng tạo. Bài viết này sẽ hướng dẫn bạn giải bài tập 9 trang 37 một cách dễ hiểu nhất.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập môn Toán.
Tìm hai số không âm a và b có tổng bằng 10 sao cho: a) Biểu thức ab đạt giá trị lớn nhất; b) Tổng bình phương của chúng đạt giá trị nhỏ nhất; c) Biểu thức (a{b^2}) đạt giá trị lớn nhất
Đề bài
Tìm hai số không âm a và b có tổng bằng 10 sao cho:
a) Biểu thức ab đạt giá trị lớn nhất;
b) Tổng bình phương của chúng đạt giá trị nhỏ nhất;
c) Biểu thức \(a{b^2}\) đạt giá trị lớn nhất
Phương pháp giải - Xem chi tiết
Tìm biểu thức liên hệ của a theo b hoặc ngược lại. Sau đó lập hàm số theo a hoặc b, lập bảng biến thiên và quan sát
Lời giải chi tiết
Ta có: a, b > 0 và a + b = 10
a) Đặt: \(f(a) = ab = a(10 - a) = - {a^2} + 10a\)
\(f'(a) = - 2a + 10 = 0 \Leftrightarrow a = 5\)
Bảng biến thiên:
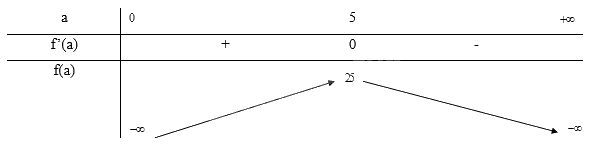
Từ bảng biến thiên ta thấy, \(\mathop {\max }\limits_{(0; + \infty )} f(a) = f(5) = 25\)
Vậy để biểu thức ab đạt giá trị lớn nhất là 25 thì a = 5 và b = 5
b) Đặt: \(f(a) = {a^2} + {b^2} = {a^2} + {(10 - a)^2} = 2{a^2} - 20a + 100\)
\(f'(a) = 4a - 20 = 0 \Leftrightarrow a = 5\)
Bảng biến thiên:
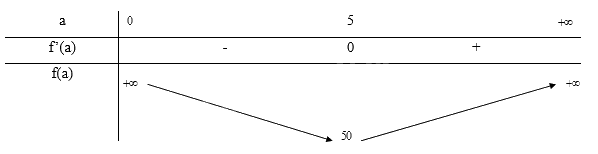
Từ bảng biến thiên ta thấy, \(\mathop {\min }\limits_{(0; + \infty )} f(a) = f(5) = 50\)
Vậy để biểu thức \({a^2} + {b^2}\) đạt giá trị nhỏ nhất là 50 thì a = 5 và b = 5
c) Đặt: \(f(a) = a{b^2} = a{(10 - a)^2} = {a^3} - 20{a^2} + 100a\)
\(f'(a) = 3{a^2} - 40a + 100 = 0 \Leftrightarrow \left[ \begin{array}{l}a = \frac{{10}}{3}\\a = 10\end{array} \right.\)
Bảng biến thiên:
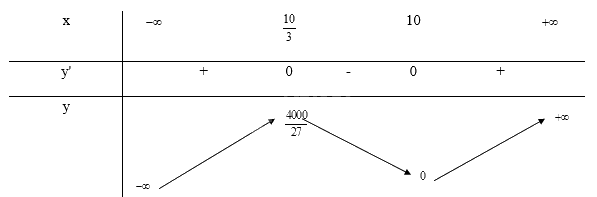
Từ bảng biến thiên ta thấy, \(\mathop {\max }\limits_{(0; + \infty )} f(a) = f(\frac{{10}}{3}) = \frac{{4000}}{{27}}\)
Vậy để biểu thức \(a{b^2}\) đạt giá trị lớn nhất là \(\frac{{4000}}{{27}}\) thì a = \(\frac{{10}}{3}\) và b = \(\frac{{20}}{3}\)
Bài tập 9 trang 37 SGK Toán 12 tập 1 - Chân trời sáng tạo thuộc chương trình học về giới hạn của hàm số. Đây là một bài tập quan trọng giúp học sinh hiểu rõ hơn về khái niệm giới hạn, cách tính giới hạn và ứng dụng của giới hạn trong việc giải quyết các bài toán thực tế.
(Nội dung đề bài sẽ được chèn vào đây - ví dụ: Tính các giới hạn sau: a) lim (x->2) (x^2 - 4)/(x - 2); b) lim (x->0) sin(3x)/x)
Để giải bài tập về giới hạn, chúng ta cần nắm vững các phương pháp sau:
(Lời giải chi tiết cho từng phần của bài tập 9 sẽ được trình bày ở đây, bao gồm các bước giải, giải thích và kết luận. Ví dụ:)
Ta có: (x^2 - 4)/(x - 2) = (x - 2)(x + 2)/(x - 2) = x + 2 (với x ≠ 2)
Vậy, lim (x->2) (x^2 - 4)/(x - 2) = lim (x->2) (x + 2) = 2 + 2 = 4
Ta có: lim (x->0) sin(3x)/x = lim (x->0) 3 * (sin(3x)/(3x)) = 3 * 1 = 3 (sử dụng giới hạn đặc biệt lim (sin x)/x = 1)
Để củng cố kiến thức về giới hạn, bạn có thể tham khảo và giải các bài tập tương tự sau:
Bài tập 9 trang 37 SGK Toán 12 tập 1 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng tính giới hạn. Hy vọng với lời giải chi tiết và các phương pháp giải được trình bày ở trên, bạn sẽ tự tin hơn trong việc giải quyết các bài tập tương tự.
Giaitoan.edu.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán. Chúc bạn học tập tốt!