Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 3 trang 46, 47, 48 SGK Toán 12 tập 1 chương trình Chân trời sáng tạo. Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và phương pháp giải bài tập hiệu quả.
Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi đã biên soạn lời giải dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải quyết các bài toán tương tự.
Tích của một số với một vectơ
Trả lời câu hỏi Thực hành 7 trang 47 SGK Toán 12 Chân trời sáng tạo
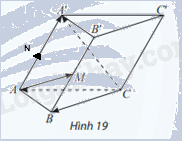
Cho hình lăng trụ ABC.A′B′C′ có M là trung điểm của BB′ (Hình 19). Đặt \(\overrightarrow {CA} = \overrightarrow a ,\overrightarrow {CB} = \overrightarrow b ,\overrightarrow {CC'} = \overrightarrow c \). Chứng minh rằng \(\overrightarrow {AM} = \overrightarrow b - \overrightarrow a + \frac{1}{2}\overrightarrow c \)
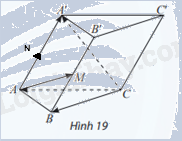
Phương pháp giải:
Áp dụng quy tắc hiệu, quy tắc hình bình hành và 2 vecto bằng nhau.
Lời giải chi tiết:
Gọi N là trung điểm AA’.
Ta có: \(\overrightarrow {CB} - \overrightarrow {CA} + \frac{1}{2}\overrightarrow {CC'} = \overrightarrow {AB} + \frac{1}{2}\overrightarrow {AA'} = \overrightarrow {AB} + \overrightarrow {AN} = \overrightarrow {AM} \)
Hay \(\overrightarrow {AM} = \overrightarrow b - \overrightarrow a + \frac{1}{2}\overrightarrow c \).
Trả lời câu hỏi Khám phá 4 trang 46 SGK Toán 12 Chân trời sáng tạo
Cho hình hộp ABCD. A′B′C′D′ có AC′ và A′C cắt nhau tại O (Hình 17).
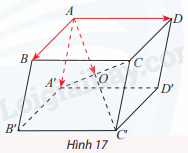
a) Tìm vectơ \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} \).
b) Cho biết mối quan hệ giữa vectơ tìm được ở câu a) và vectơ \(\overrightarrow {AO} \).
Phương pháp giải:
Áp dụng quy tắc hình hộp.
Lời giải chi tiết:
a) \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \).
b) \(\overrightarrow {AC'} = 2\overrightarrow {AO} \).
Trả lời câu hỏi Vận dụng 3 trang 48 SGK Toán 12 Chân trời sáng tạo
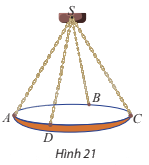
Một chiếc đèn chùm treo có khối lượng m = 5 kg được thiết kế với đĩa đèn được giữ bởi bốn đoạn xích SA, SB, SC, SD sao cho S.ABCD là hình chóp tứ giác đều có \(\widehat {ASC} = 60^\circ \) (Hình 21).
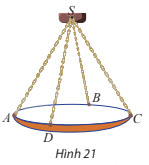
a) Sử dụng công thức \(\overrightarrow P = m\overrightarrow g \) trong đó \(\overrightarrow g \) là vectơ gia tốc rơi tự do có độ lớn 10\(m/{s^2}\), tìm độ lớn của trọng lực \(\overrightarrow P \) tác động lên chiếc đèn chùm.
b) Tìm độ lớn của lực căng cho mỗi sợi xích.
Phương pháp giải:
a) Áp dụng công thức tính trọng lực.
b) Để chiếc đèn cân bằng thì hợp lực của 4 sợi xích phải cân bằng với trọng lực. Dựa vào tính chất của hình chóp tứ giác đều và quy tắc hình bình hành để tìm hợp lực đó rồi tìm ra lực căng của mỗi sợi xích.
Lời giải chi tiết:
a) Độ lớn trọng lực tác động lên đèn chùm là: P = mg = 5.10 = 50 (N).
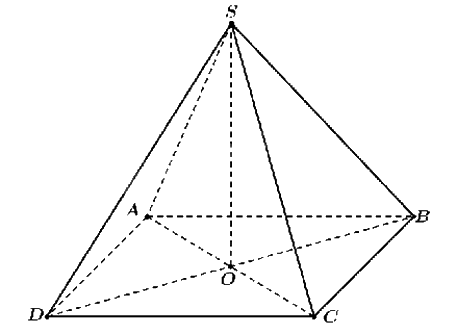
b) Giả sử đèn chùm được minh họa như hình vẽ trên.
Gọi O là tâm hình vuông ABCD.
Ta có \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \)
\( \Leftrightarrow \overrightarrow {OS} + \overrightarrow {SA} + \overrightarrow {OS} + \overrightarrow {SB} + \overrightarrow {OS} + \overrightarrow {SC} + \overrightarrow {OS} + \overrightarrow {SD} = \overrightarrow 0 \)
\( \Leftrightarrow \overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = - 4\overrightarrow {OS} = 4\overrightarrow {SO} \)
\( \Rightarrow \left| {\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} } \right| = \left| {4\overrightarrow {SO} } \right| = 4SO\).
Trọng lượng của vật là \(P = 50\) (N).
Suy ra \(4\left| {\overrightarrow {SO} } \right| = P = 50\). Do đó \(SO = \frac{{50}}{4} = \frac{{25}}{2}\).
Vì \(\widehat {ASC} = {60^o}\) suy ra \(\widehat {ASO} = {30^o}\).
Xét tam giác SAO vuông tại O:
\(\cos \widehat {ASO} = \frac{{SO}}{{SA}} \Leftrightarrow SA = \frac{{SO}}{{\cos \widehat {ASO}}} = \frac{{\frac{{25}}{2}}}{{\cos {{30}^o}}} = \frac{{25\sqrt 3 }}{3}\).
Vậy lực tác dụng lên mỗi sợi dây xích bằng \(\frac{{25\sqrt 3 }}{3}\) (N).
Trả lời câu hỏi Khám phá 4 trang 46 SGK Toán 12 Chân trời sáng tạo
Cho hình hộp ABCD. A′B′C′D′ có AC′ và A′C cắt nhau tại O (Hình 17).
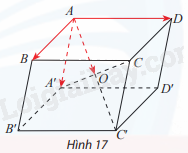
a) Tìm vectơ \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} \).
b) Cho biết mối quan hệ giữa vectơ tìm được ở câu a) và vectơ \(\overrightarrow {AO} \).
Phương pháp giải:
Áp dụng quy tắc hình hộp.
Lời giải chi tiết:
a) \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \).
b) \(\overrightarrow {AC'} = 2\overrightarrow {AO} \).
Trả lời câu hỏi Thực hành 7 trang 47 SGK Toán 12 Chân trời sáng tạo
Cho hình lăng trụ ABC.A′B′C′ có M là trung điểm của BB′ (Hình 19). Đặt \(\overrightarrow {CA} = \overrightarrow a ,\overrightarrow {CB} = \overrightarrow b ,\overrightarrow {CC'} = \overrightarrow c \). Chứng minh rằng \(\overrightarrow {AM} = \overrightarrow b - \overrightarrow a + \frac{1}{2}\overrightarrow c \)
Phương pháp giải:
Áp dụng quy tắc hiệu, quy tắc hình bình hành và 2 vecto bằng nhau.
Lời giải chi tiết:
Gọi N là trung điểm AA’.
Ta có: \(\overrightarrow {CB} - \overrightarrow {CA} + \frac{1}{2}\overrightarrow {CC'} = \overrightarrow {AB} + \frac{1}{2}\overrightarrow {AA'} = \overrightarrow {AB} + \overrightarrow {AN} = \overrightarrow {AM} \)
Hay \(\overrightarrow {AM} = \overrightarrow b - \overrightarrow a + \frac{1}{2}\overrightarrow c \).
Trả lời câu hỏi Vận dụng 3 trang 48 SGK Toán 12 Chân trời sáng tạo
Một chiếc đèn chùm treo có khối lượng m = 5 kg được thiết kế với đĩa đèn được giữ bởi bốn đoạn xích SA, SB, SC, SD sao cho S.ABCD là hình chóp tứ giác đều có \(\widehat {ASC} = 60^\circ \) (Hình 21).
a) Sử dụng công thức \(\overrightarrow P = m\overrightarrow g \) trong đó \(\overrightarrow g \) là vectơ gia tốc rơi tự do có độ lớn 10\(m/{s^2}\), tìm độ lớn của trọng lực \(\overrightarrow P \) tác động lên chiếc đèn chùm.
b) Tìm độ lớn của lực căng cho mỗi sợi xích.
Phương pháp giải:
a) Áp dụng công thức tính trọng lực.
b) Để chiếc đèn cân bằng thì hợp lực của 4 sợi xích phải cân bằng với trọng lực. Dựa vào tính chất của hình chóp tứ giác đều và quy tắc hình bình hành để tìm hợp lực đó rồi tìm ra lực căng của mỗi sợi xích.
Lời giải chi tiết:
a) Độ lớn trọng lực tác động lên đèn chùm là: P = mg = 5.10 = 50 (N).
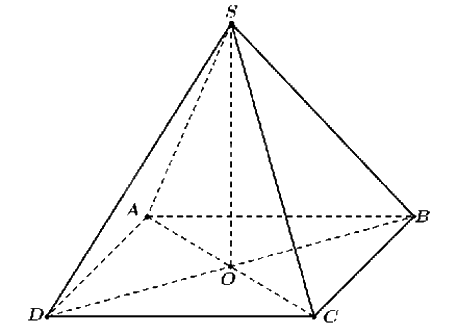
b) Giả sử đèn chùm được minh họa như hình vẽ trên.
Gọi O là tâm hình vuông ABCD.
Ta có \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \)
\( \Leftrightarrow \overrightarrow {OS} + \overrightarrow {SA} + \overrightarrow {OS} + \overrightarrow {SB} + \overrightarrow {OS} + \overrightarrow {SC} + \overrightarrow {OS} + \overrightarrow {SD} = \overrightarrow 0 \)
\( \Leftrightarrow \overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = - 4\overrightarrow {OS} = 4\overrightarrow {SO} \)
\( \Rightarrow \left| {\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} } \right| = \left| {4\overrightarrow {SO} } \right| = 4SO\).
Trọng lượng của vật là \(P = 50\) (N).
Suy ra \(4\left| {\overrightarrow {SO} } \right| = P = 50\). Do đó \(SO = \frac{{50}}{4} = \frac{{25}}{2}\).
Vì \(\widehat {ASC} = {60^o}\) suy ra \(\widehat {ASO} = {30^o}\).
Xét tam giác SAO vuông tại O:
\(\cos \widehat {ASO} = \frac{{SO}}{{SA}} \Leftrightarrow SA = \frac{{SO}}{{\cos \widehat {ASO}}} = \frac{{\frac{{25}}{2}}}{{\cos {{30}^o}}} = \frac{{25\sqrt 3 }}{3}\).
Vậy lực tác dụng lên mỗi sợi dây xích bằng \(\frac{{25\sqrt 3 }}{3}\) (N).
Mục 3 trong SGK Toán 12 tập 1 chương trình Chân trời sáng tạo tập trung vào việc nghiên cứu về đạo hàm của hàm số. Đây là một phần kiến thức nền tảng và quan trọng trong chương trình Toán học lớp 12, đóng vai trò then chốt trong việc giải quyết các bài toán liên quan đến cực trị, đơn điệu của hàm số và ứng dụng của đạo hàm trong nhiều lĩnh vực khác.
Mục 3 bao gồm các nội dung chính sau:
Trang 46 SGK Toán 12 tập 1 Chân trời sáng tạo chứa các bài tập vận dụng các kiến thức về định nghĩa đạo hàm để tính đạo hàm của các hàm số đơn giản. Các bài tập này giúp học sinh làm quen với việc áp dụng các quy tắc tính đạo hàm và rèn luyện kỹ năng tính toán.
Ví dụ, bài 1 yêu cầu tính đạo hàm của hàm số f(x) = x2 + 3x - 2. Áp dụng quy tắc đạo hàm của tổng và đạo hàm của hàm lũy thừa, ta có:
f'(x) = 2x + 3
Trang 47 tập trung vào việc tính đạo hàm của các hàm số phức tạp hơn, đòi hỏi học sinh phải vận dụng linh hoạt các quy tắc tính đạo hàm và kết hợp chúng một cách hợp lý. Các bài tập này thường liên quan đến hàm hợp và các phép biến đổi đại số.
Ví dụ, bài 2 yêu cầu tính đạo hàm của hàm số g(x) = sin(2x). Áp dụng quy tắc đạo hàm của hàm hợp, ta có:
g'(x) = cos(2x) * 2 = 2cos(2x)
Trang 48 chứa các bài tập ứng dụng đạo hàm để giải quyết các bài toán thực tế. Các bài tập này thường liên quan đến việc tìm cực trị của hàm số và xét tính đơn điệu của hàm số.
Ví dụ, bài 3 yêu cầu tìm cực trị của hàm số h(x) = x3 - 3x2 + 2. Để tìm cực trị, ta thực hiện các bước sau:
Việc nắm vững kiến thức về đạo hàm là rất quan trọng đối với học sinh lớp 12. Hy vọng rằng với lời giải chi tiết và các lời khuyên trên, các em sẽ tự tin giải quyết các bài tập trong Mục 3 SGK Toán 12 tập 1 chương trình Chân trời sáng tạo và đạt kết quả tốt trong môn Toán.