Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 3 trang 28, 29, 30 sách giáo khoa Toán 12 tập 1 chương trình Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Khảo sát hàm số \(y = \frac{{ax + b}}{{cx + d}}(c \ne 0,ad - bc \ne 0)\)
Trả lời câu hỏi Thực hành 2 trang 30 SGK Toán 12 Chân trời sáng tạo
Khảo sát và vẽ đồ thị của các hàm số sau:
a) \(y = \frac{{x + 1}}{{x - 1}}\)
b) \(y = \frac{{2x}}{{3x - 1}}\)
c) \(y = \frac{{5 + x}}{{2 - x}}\)
Phương pháp giải:
Bước 1. Tìm tập xác định của hàm số
Bước 2. Xét sự biến thiên của hàm số
− Tìm đạo hàm y', xét dấu y', xác định khoảng đơn điệu của hàm số.
− Tìm các tiệm cận của đồ thị hàm số
− Lập bảng biến thiên của hàm số.
Bước 3. Vẽ đồ thị của hàm số
− Xác định các giao điểm của đồ thị với các trục toạ độ
− Vẽ các đường tiệm cận của đồ thị hàm số (nếu có).
− Vẽ đồ thị hàm số.
Lời giải chi tiết:
a) \(y = \frac{{x + 1}}{{x - 1}}\)
Tập xác định: \(D = \mathbb{R}\backslash \{ 1\} \)
\(y' = \frac{{ - 2}}{{{{(x - 1)}^2}}} \le 0\forall x \in D\)nên hàm số nghịch biến trên D
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \frac{{x + 1}}{{x - 1}} = 1;\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \frac{{x + 1}}{{x - 1}} = 1\) nên y = 1 là tiệm cận ngang của đồ thị hàm số
\(\mathop {\lim }\limits_{x \to {1^ + }} y = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{x + 1}}{{x - 1}} = + \infty ;\mathop {\lim }\limits_{x \to {1^ - }} y = \mathop {\lim }\limits_{x \to {1^ - }} \frac{{x + 1}}{{x - 1}} = - \infty \) nên x = 1 là tiệm cận đứng của đồ thị hàm số
Bảng biến thiên: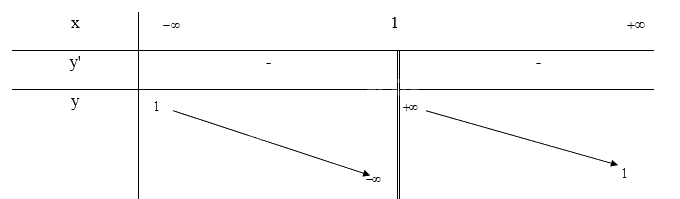
Khi x = 0 thì y = -1 nên (0; -1) là giao điểm của đồ thị với trục Oy
Ta có: \(y = 0 \Leftrightarrow \frac{{x + 1}}{{x - 1}} = 0 \Leftrightarrow x = - 1\)
Vậy đồ thị của hàm số giao với trục Ox tại điểm (-1; 0)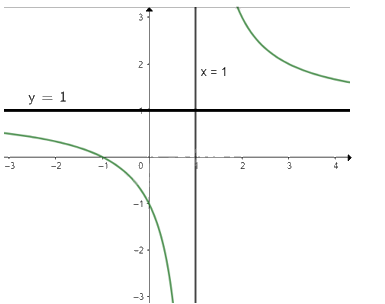
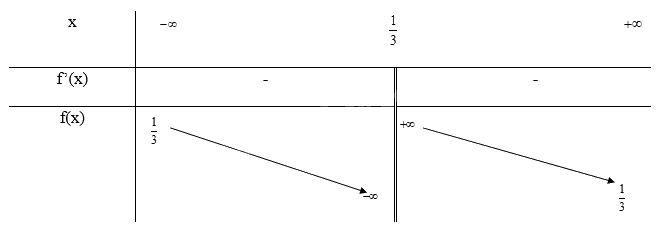
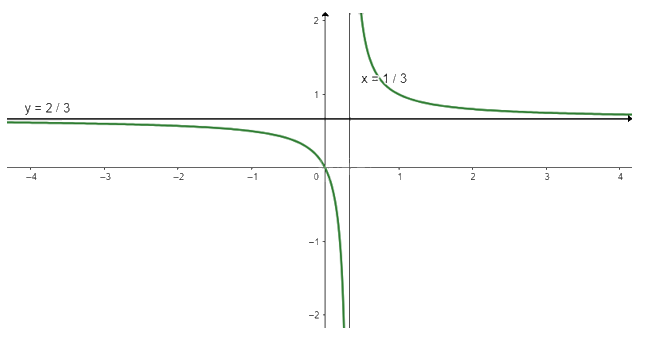
b) \(y = \frac{{2x}}{{3x - 1}}\)
Tập xác định: \(D = \mathbb{R}\backslash \{ \frac{1}{3}\} \)
\(y' = \frac{{ - 2}}{{{{(3x - 1)}^2}}} \le 0\forall x \in D\) nên hàm số nghịch biến trên D
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \frac{{2x}}{{3x - 1}} = \frac{2}{3};\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \frac{{2x}}{{3x - 1}} = \frac{2}{3}\) nên y = \(\frac{2}{3}\) là tiệm cận ngang của đồ thị hàm số
\(\mathop {\lim }\limits_{x \to {{\frac{1}{3}}^ + }} y = \mathop {\lim }\limits_{x \to {{\frac{1}{3}}^ + }} \frac{{2x}}{{3x - 1}} = + \infty ;\mathop {\lim }\limits_{x \to {{\frac{1}{3}}^ - }} y = \mathop {\lim }\limits_{x \to {{\frac{1}{3}}^ - }} \frac{{2x}}{{3x - 1}} = - \infty \) nên x = \(\frac{1}{3}\) là tiệm cận đứng của đồ thị hàm số
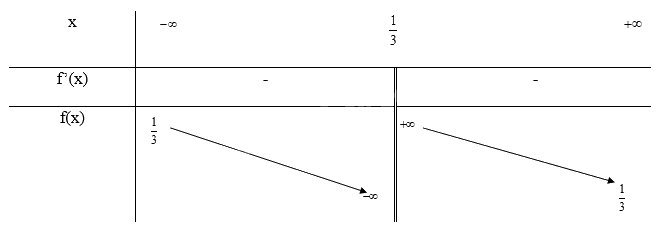
Khi x = 0 thì y = 0 nên (0; 0) là giao điểm của đồ thị với trục Oy
Ta có: \(y = 0 \Leftrightarrow \frac{{2x}}{{3x - 1}} = 0 \Leftrightarrow x = 0\)
Vậy đồ thị của hàm số giao với trục Ox tại điểm (0; 0)
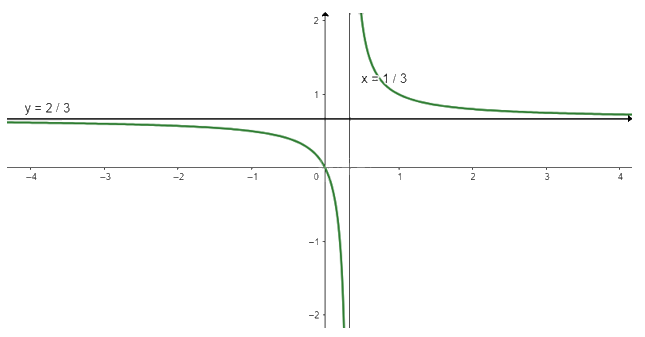
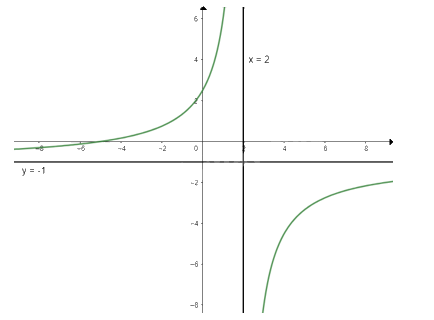
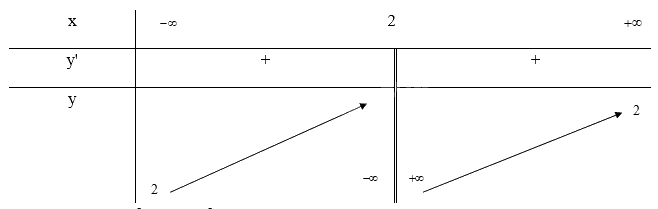
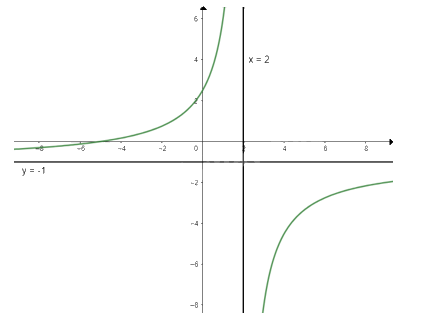
c) \(y = \frac{{5 + x}}{{2 - x}}\)
Tập xác định: \(D = \mathbb{R}\backslash \{ 2\} \)
\(y' = \frac{7}{{{{(2 - x)}^2}}} \ge 0\forall x \in D\) nên hàm số đồng biến trên D
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \frac{{5 + x}}{{2 - x}} = - 1;\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \frac{{5 + x}}{{2 - x}} = - 1\) nên y = -1 là tiệm cận ngang của đồ thị hàm số
\(\mathop {\lim }\limits_{x \to {2^ + }} y = \mathop {\lim }\limits_{x \to {2^ + }} y = \frac{{5 + x}}{{2 - x}} = - \infty ;\mathop {\lim }\limits_{x \to {2^ - }} y = \mathop {\lim }\limits_{x \to {2^ - }} \frac{{2x}}{{3x - 1}} = + \infty \) nên x = 2 là tiệm cận đứng của đồ thị hàm số
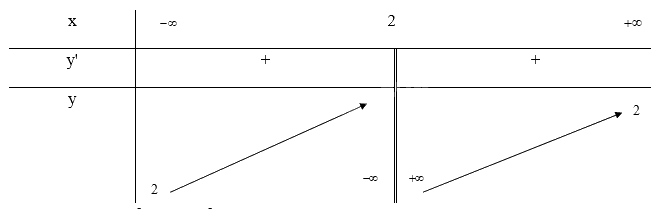
Khi x = 0 thì y = \(\frac{5}{2}\) nên (0; \(\frac{5}{2}\)) là giao điểm của đồ thị với trục Oy
Ta có: \(y = 0 \Leftrightarrow \frac{{5 + x}}{{2 - x}} = 0 \Leftrightarrow x = - 5\)
Vậy đồ thị của hàm số giao với trục Ox tại điểm (-5; 0)
Trả lời câu hỏi Thực hành 2 trang 30 SGK Toán 12 Chân trời sáng tạo
Khảo sát và vẽ đồ thị của các hàm số sau:
a) \(y = \frac{{x + 1}}{{x - 1}}\)
b) \(y = \frac{{2x}}{{3x - 1}}\)
c) \(y = \frac{{5 + x}}{{2 - x}}\)
Phương pháp giải:
Bước 1. Tìm tập xác định của hàm số
Bước 2. Xét sự biến thiên của hàm số
− Tìm đạo hàm y', xét dấu y', xác định khoảng đơn điệu của hàm số.
− Tìm các tiệm cận của đồ thị hàm số
− Lập bảng biến thiên của hàm số.
Bước 3. Vẽ đồ thị của hàm số
− Xác định các giao điểm của đồ thị với các trục toạ độ
− Vẽ các đường tiệm cận của đồ thị hàm số (nếu có).
− Vẽ đồ thị hàm số.
Lời giải chi tiết:
a) \(y = \frac{{x + 1}}{{x - 1}}\)
Tập xác định: \(D = \mathbb{R}\backslash \{ 1\} \)
\(y' = \frac{{ - 2}}{{{{(x - 1)}^2}}} \le 0\forall x \in D\)nên hàm số nghịch biến trên D
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \frac{{x + 1}}{{x - 1}} = 1;\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \frac{{x + 1}}{{x - 1}} = 1\) nên y = 1 là tiệm cận ngang của đồ thị hàm số
\(\mathop {\lim }\limits_{x \to {1^ + }} y = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{x + 1}}{{x - 1}} = + \infty ;\mathop {\lim }\limits_{x \to {1^ - }} y = \mathop {\lim }\limits_{x \to {1^ - }} \frac{{x + 1}}{{x - 1}} = - \infty \) nên x = 1 là tiệm cận đứng của đồ thị hàm số
Bảng biến thiên: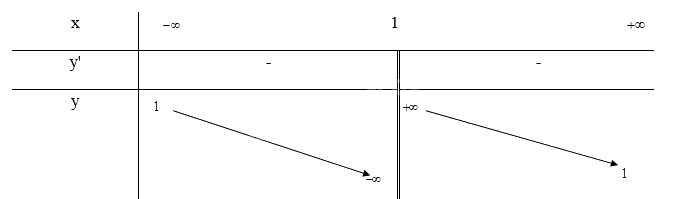
Khi x = 0 thì y = -1 nên (0; -1) là giao điểm của đồ thị với trục Oy
Ta có: \(y = 0 \Leftrightarrow \frac{{x + 1}}{{x - 1}} = 0 \Leftrightarrow x = - 1\)
Vậy đồ thị của hàm số giao với trục Ox tại điểm (-1; 0)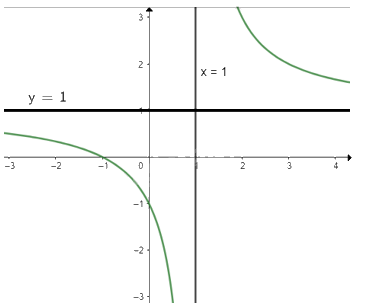
b) \(y = \frac{{2x}}{{3x - 1}}\)
Tập xác định: \(D = \mathbb{R}\backslash \{ \frac{1}{3}\} \)
\(y' = \frac{{ - 2}}{{{{(3x - 1)}^2}}} \le 0\forall x \in D\) nên hàm số nghịch biến trên D
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \frac{{2x}}{{3x - 1}} = \frac{2}{3};\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \frac{{2x}}{{3x - 1}} = \frac{2}{3}\) nên y = \(\frac{2}{3}\) là tiệm cận ngang của đồ thị hàm số
\(\mathop {\lim }\limits_{x \to {{\frac{1}{3}}^ + }} y = \mathop {\lim }\limits_{x \to {{\frac{1}{3}}^ + }} \frac{{2x}}{{3x - 1}} = + \infty ;\mathop {\lim }\limits_{x \to {{\frac{1}{3}}^ - }} y = \mathop {\lim }\limits_{x \to {{\frac{1}{3}}^ - }} \frac{{2x}}{{3x - 1}} = - \infty \) nên x = \(\frac{1}{3}\) là tiệm cận đứng của đồ thị hàm số
Khi x = 0 thì y = 0 nên (0; 0) là giao điểm của đồ thị với trục Oy
Ta có: \(y = 0 \Leftrightarrow \frac{{2x}}{{3x - 1}} = 0 \Leftrightarrow x = 0\)
Vậy đồ thị của hàm số giao với trục Ox tại điểm (0; 0)
c) \(y = \frac{{5 + x}}{{2 - x}}\)
Tập xác định: \(D = \mathbb{R}\backslash \{ 2\} \)
\(y' = \frac{7}{{{{(2 - x)}^2}}} \ge 0\forall x \in D\) nên hàm số đồng biến trên D
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \frac{{5 + x}}{{2 - x}} = - 1;\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \frac{{5 + x}}{{2 - x}} = - 1\) nên y = -1 là tiệm cận ngang của đồ thị hàm số
\(\mathop {\lim }\limits_{x \to {2^ + }} y = \mathop {\lim }\limits_{x \to {2^ + }} y = \frac{{5 + x}}{{2 - x}} = - \infty ;\mathop {\lim }\limits_{x \to {2^ - }} y = \mathop {\lim }\limits_{x \to {2^ - }} \frac{{2x}}{{3x - 1}} = + \infty \) nên x = 2 là tiệm cận đứng của đồ thị hàm số
Khi x = 0 thì y = \(\frac{5}{2}\) nên (0; \(\frac{5}{2}\)) là giao điểm của đồ thị với trục Oy
Ta có: \(y = 0 \Leftrightarrow \frac{{5 + x}}{{2 - x}} = 0 \Leftrightarrow x = - 5\)
Vậy đồ thị của hàm số giao với trục Ox tại điểm (-5; 0)
Mục 3 trong SGK Toán 12 tập 1 chương trình Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết các bài tập trong mục này một cách hiệu quả, học sinh cần nắm vững lý thuyết, công thức và phương pháp giải liên quan. Bài viết này sẽ đi sâu vào từng bài tập, cung cấp lời giải chi tiết và phân tích các bước giải để giúp học sinh hiểu rõ hơn về cách tiếp cận và giải quyết vấn đề.
Bài tập này thường yêu cầu học sinh vận dụng kiến thức về... (giả sử bài tập liên quan đến giới hạn). Để giải bài tập này, ta cần:
Lời giải chi tiết:
...
Bài tập này có thể liên quan đến... (giả sử bài tập liên quan đến đạo hàm). Để giải quyết bài tập này, chúng ta cần:
Lời giải chi tiết:
...
Bài tập này yêu cầu... (giả sử bài tập liên quan đến ứng dụng đạo hàm để khảo sát hàm số). Các bước giải quyết:
Lời giải chi tiết:
...
Bài tập này tập trung vào... (giả sử bài tập liên quan đến tối ưu hóa). Để giải bài toán tối ưu hóa, ta cần:
Lời giải chi tiết:
...
Trong quá trình giải bài tập, học sinh cần lưu ý một số điểm sau:
Để học tập và ôn luyện Toán 12 hiệu quả, học sinh có thể tham khảo các tài liệu sau:
Hy vọng rằng bài viết này đã cung cấp cho các em học sinh những kiến thức và kỹ năng cần thiết để giải quyết các bài tập trong mục 3 trang 28,29,30 SGK Toán 12 tập 1 chương trình Chân trời sáng tạo. Chúc các em học tập tốt và đạt kết quả cao trong kỳ thi sắp tới!