Giải bài tập 3 trang 75 SGK Toán 12 tập 2 - Chân trời sáng tạo

Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập Toán 12 tập 2. Bài viết này sẽ hướng dẫn bạn giải bài tập 3 trang 75 SGK Toán 12 tập 2 theo chương trình Chân trời sáng tạo.

Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi đã biên soạn lời giải một cách dễ hiểu, kèm theo các bước giải chi tiết để giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.

Mỗi bạn học sinh trong lớp của Minh lựa chọn học một trong hai ngoại ngữ là tiếng Anh hoặc tiếng Nhật. Xác suất chọn tiếng Anh của mỗi bạn học sinh nữ là 0,6 và của mỗi bạn học sinh nam là 0,7. Lớp của Minh có 25 bạn nữ và 20 bạn nam. Chọn ra ngẫu nhiên một bạn trong lớp. Sử dụng sơ đồ hình cây, tính xác suất của các biến cố: \(A\): “Bạn được chọn là nam và học tiếng Nhật” \(B\): “Bạn được chọn là nữ và học tiếng Anh”

Đề bài

Sử dụng sơ đồ hình cây, tính xác suất của các biến cố:

\(A\): “Bạn được chọn là nam và học tiếng Nhật”

\(B\): “Bạn được chọn là nữ và học tiếng Anh”

Phương pháp giải - Xem chi tiết Giải bài tập 3 trang 75 SGK Toán 12 tập 2 - Chân trời sáng tạo 1

Gọi \(M\) là biến cố “Bạn được chọn là nam”, \(N\) là biến cố “Bạn được chọn học tiếng Anh”. Sử dụng sơ đồ hình cây, từ đó tính được \(P\left( A \right)\) và \(P\left( B \right)\).

Lời giải chi tiết

Gọi \(M\) là biến cố “Bạn được chọn là nam”, \(N\) là biến cố “Bạn được chọn học tiếng Anh”. Lớp có 25 bạn nữ và 20 bạn nam nên xác suất chọn được 1 bạn nam là \(P\left( M \right) = \frac{{20}}{{45}} = \frac{4}{9}\). Từ đó, ta có sơ đồ hình cây sau:

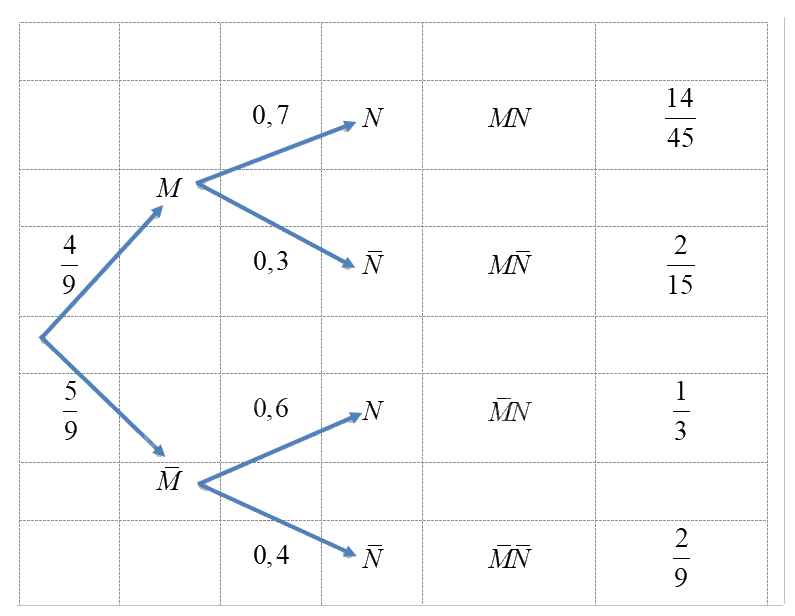
Giải bài tập 3 trang 75 SGK Toán 12 tập 2 - Chân trời sáng tạo 2

Từ sơ đồ hình cây, suy ra:

\(P\left( A \right) = P\left( {M\bar N} \right) = \frac{2}{{15}}\) và \(P\left( B \right) = P\left( {\bar MN} \right) = \frac{1}{3}.\)

Tự tin bứt phá Kỳ thi THPT Quốc gia môn Toán! Đừng bỏ lỡ Giải bài tập 3 trang 75 SGK Toán 12 tập 2 - Chân trời sáng tạo đặc sắc thuộc chuyên mục đề thi toán 12 trên nền tảng toán. Với bộ bài tập lý thuyết toán thpt được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình Toán 12, đây chính là "chiến lược vàng" giúp các em tối ưu hóa ôn luyện. Học sinh sẽ không chỉ làm chủ mọi dạng bài thi mà còn nắm vững chiến thuật làm bài hiệu quả, sẵn sàng tự tin chinh phục điểm cao, vững bước vào đại học mơ ước nhờ phương pháp học trực quan, khoa học và hiệu quả học tập vượt trội!

Giải bài tập 3 trang 75 SGK Toán 12 tập 2 - Chân trời sáng tạo: Tổng quan

Bài tập 3 trang 75 SGK Toán 12 tập 2 thuộc chương trình Chân trời sáng tạo tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế liên quan đến tốc độ thay đổi của một đại lượng. Bài tập này thường yêu cầu học sinh phải hiểu rõ các khái niệm như đạo hàm, quy tắc tính đạo hàm, và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.

Nội dung bài tập 3 trang 75 SGK Toán 12 tập 2 - Chân trời sáng tạo

Bài tập 3 thường bao gồm các dạng bài sau:

Dạng 1: Xác định đạo hàm của hàm số và tính giá trị đạo hàm tại một điểm cho trước.
Dạng 2: Tìm đạo hàm của hàm hợp.
Dạng 3: Vận dụng đạo hàm để giải các bài toán về tốc độ thay đổi, chẳng hạn như tốc độ tăng trưởng dân số, tốc độ thay đổi của sản lượng, v.v.
Dạng 4: Sử dụng đạo hàm để tìm cực trị của hàm số.

Lời giải chi tiết bài tập 3 trang 75 SGK Toán 12 tập 2 - Chân trời sáng tạo

Để giúp bạn hiểu rõ hơn về cách giải bài tập này, chúng tôi sẽ trình bày lời giải chi tiết cho từng câu hỏi. Lưu ý rằng, trước khi bắt đầu giải bài tập, bạn nên ôn lại các kiến thức lý thuyết liên quan đến đạo hàm và ứng dụng của đạo hàm.

Ví dụ minh họa (Giả định một bài tập cụ thể):

Bài tập: Cho hàm số f(x) = x³ - 3x² + 2. Tìm đạo hàm f'(x) và tính f'(1).

Lời giải:

Bước 1: Tính đạo hàm f'(x) bằng quy tắc tính đạo hàm của tổng và tích.
f'(x) = 3x² - 6x
Bước 2: Thay x = 1 vào f'(x) để tính f'(1).
f'(1) = 3(1)² - 6(1) = -3
Kết luận: Đạo hàm f'(x) = 3x² - 6x và f'(1) = -3.

Mẹo giải bài tập đạo hàm hiệu quả

Để giải bài tập đạo hàm một cách hiệu quả, bạn có thể tham khảo một số mẹo sau:

Nắm vững các quy tắc tính đạo hàm cơ bản: Quy tắc tính đạo hàm của tổng, hiệu, tích, thương, hàm hợp, v.v.
Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để làm quen với các dạng bài và rèn luyện kỹ năng giải toán.
Sử dụng các công cụ hỗ trợ: Sử dụng máy tính cầm tay hoặc các phần mềm tính đạo hàm để kiểm tra kết quả và tiết kiệm thời gian.
Hiểu rõ bản chất của đạo hàm: Đạo hàm biểu thị tốc độ thay đổi của một hàm số tại một điểm.

Ứng dụng của đạo hàm trong thực tế

Đạo hàm có rất nhiều ứng dụng trong thực tế, chẳng hạn như:

Vật lý: Tính vận tốc, gia tốc, lực, v.v.
Kinh tế: Tính chi phí biên, doanh thu biên, lợi nhuận biên, v.v.
Kỹ thuật: Tối ưu hóa thiết kế, điều khiển hệ thống, v.v.
Thống kê: Phân tích dữ liệu, dự đoán xu hướng, v.v.

Tổng kết

Bài tập 3 trang 75 SGK Toán 12 tập 2 - Chân trời sáng tạo là một bài tập quan trọng giúp bạn củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm. Hy vọng rằng, với lời giải chi tiết và các mẹo giải bài tập mà chúng tôi đã cung cấp, bạn sẽ tự tin hơn trong quá trình học tập và giải quyết các bài toán liên quan đến đạo hàm.

Hãy tiếp tục luyện tập và khám phá thêm nhiều kiến thức thú vị về toán học tại giaitoan.edu.vn!