Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12. Bài viết này sẽ hướng dẫn bạn giải bài tập 7 trang 57 SGK Toán 12 tập 1 - Chân trời sáng tạo một cách nhanh chóng và hiệu quả.
Chúng tôi cam kết mang đến cho bạn những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và đạt kết quả cao trong môn Toán.
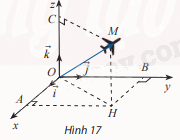
Ở một sân bay, ví trí của máy bay được xác định bởi điểm M trong không gian Oxyz như Hình 17. Gọi H là hình chiếu vuông góc của M xuống mặt phẳng (Oxy). Cho biết OM = 50, ((overrightarrow i ;overrightarrow {OH} ) = 64^circ ), ((overrightarrow {OH} ;overrightarrow {OM} ) = 48^circ ). Tìm toạ độ của điểm M.
Đề bài
Ở một sân bay, ví trí của máy bay được xác định bởi điểm M trong không gian Oxyz như Hình 17. Gọi H là hình chiếu vuông góc của M xuống mặt phẳng (Oxy). Cho biết OM = 50, \((\overrightarrow i ;\overrightarrow {OH} ) = 64^\circ \), \((\overrightarrow {OH} ;\overrightarrow {OM} ) = 48^\circ \). Tìm toạ độ của điểm M.
Phương pháp giải - Xem chi tiết
Áp dụng hệ thức về cạnh và góc trong tam giác vuông để tìm hoành độ, tung độ và cao độ của M.
Lời giải chi tiết
Ta có: \(OC = MH = OM.\sin (\overrightarrow {OH} ;\overrightarrow {OM} ) = 50.\sin 48^\circ \approx 37,16\)
\(OH = OM.\cos (\overrightarrow {OH} ;\overrightarrow {OM} ) = 50.\cos 48^\circ = 50.\cos 48^\circ \approx 33,46\)
\(OA = OH.\cos (\overrightarrow i ;\overrightarrow {OH} ) = 33,46.\cos 64^\circ = 33,46.\cos 64^\circ \approx 14,67\)
\(OB = OH.\cos (90^\circ - (\overrightarrow i ;\overrightarrow {OH} )) = 33,46.\cos (90^\circ - 64^\circ ) = 33,46.\cos 26^\circ \approx 30,07\)
\(\Rightarrow M(14,67; 30,07; 37,16)\).
Bài tập 7 trang 57 SGK Toán 12 tập 1 - Chân trời sáng tạo thuộc chương trình học về giới hạn của hàm số. Bài tập này yêu cầu học sinh vận dụng kiến thức về giới hạn một bên, giới hạn tại một điểm và các tính chất của giới hạn để giải quyết các bài toán cụ thể. Việc nắm vững kiến thức nền tảng và kỹ năng giải bài tập là rất quan trọng để học tốt môn Toán 12.
Bài tập 7 bao gồm các câu hỏi liên quan đến việc tính giới hạn của hàm số tại một điểm, sử dụng định nghĩa và các tính chất của giới hạn. Các hàm số thường gặp trong bài tập này là hàm đa thức, hàm phân thức và các hàm số đặc biệt khác. Để giải quyết bài tập này, học sinh cần:
Dưới đây là lời giải chi tiết cho từng câu hỏi trong bài tập 7 trang 57 SGK Toán 12 tập 1 - Chân trời sáng tạo:
Để giải câu a, ta cần tính giới hạn của hàm số f(x) khi x tiến tới một giá trị cụ thể. Ta có thể sử dụng định nghĩa giới hạn hoặc các tính chất của giới hạn để tìm ra kết quả.
Ví dụ:
lim (x->2) (x^2 - 4) / (x - 2) = lim (x->2) (x + 2) = 4Tương tự như câu a, ta cần tính giới hạn của hàm số f(x) khi x tiến tới một giá trị khác. Trong trường hợp này, ta có thể sử dụng phương pháp nhân liên hợp để đơn giản hóa biểu thức và tính giới hạn.
Ví dụ:
lim (x->0) (sqrt(x + 1) - 1) / x = lim (x->0) (x + 1 - 1) / (x * (sqrt(x + 1) + 1)) = lim (x->0) 1 / (sqrt(x + 1) + 1) = 1/2Câu c có thể yêu cầu tính giới hạn của một hàm số phức tạp hơn, đòi hỏi học sinh phải vận dụng nhiều kiến thức và kỹ năng khác nhau. Trong trường hợp này, ta có thể sử dụng định lý giới hạn hoặc các phương pháp biến đổi đại số để tìm ra kết quả.
Ngoài bài tập 7, còn rất nhiều bài tập tương tự về giới hạn hàm số trong SGK Toán 12 tập 1 - Chân trời sáng tạo. Để giải quyết các bài tập này, học sinh cần:
Kiến thức về giới hạn hàm số có ứng dụng rất lớn trong nhiều lĩnh vực khác nhau của toán học và khoa học kỹ thuật, như:
Bài tập 7 trang 57 SGK Toán 12 tập 1 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về giới hạn hàm số. Hy vọng rằng với lời giải chi tiết và các hướng dẫn trên, bạn sẽ giải quyết bài tập này một cách dễ dàng và hiệu quả. Chúc bạn học tốt!