Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tập 1 của giaitoan.edu.vn. Chúng tôi xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 3 trang 22, 23, 24 sách giáo khoa Toán 12 tập 1 chương trình Chân trời sáng tạo.
Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi cam kết cung cấp những lời giải chính xác, đầy đủ và giúp các em nắm vững kiến thức.
Đường tiệm cận xiên
Trả lời câu hỏi Thực hành 3 trang 24 SGK Toán 12 Chân trời sáng tạo
Tìm tiệm cận xiên của đồ thị hàm số \(y = \frac{{2{x^2} - 3x}}{{x + 5}}\)
Phương pháp giải:
Đường thẳng y = ax + b, a ≠ 0, được gọi là đường tiệm cận xiên (hay tiệm cận xiên) của đồ thị hàm số y = f(x) nếu \(\mathop {\lim }\limits_{x \to - \infty } [f(x) - (ax + b)] = 0\) hoặc \(\mathop {\lim }\limits_{x \to + \infty } [f(x) - (ax + b)] = 0\)
Lời giải chi tiết:
Tập xác định: \(D = \mathbb{R}\backslash \left\{ { - 5} \right\}\)
Ta có: \(a = \mathop {\lim }\limits_{x \to + \infty } \frac{y}{x} = \mathop {\lim }\limits_{x \to + \infty } \frac{{\frac{{2{x^2} - 3x}}{{x + 5}}}}{x} = \mathop {\lim }\limits_{x \to + \infty } \frac{{2{x^2} - 3x}}{{{x^2} + 5x}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{2 - \frac{3}{x}}}{{1 + \frac{5}{x}}} = 2\)
\(b = \mathop {\lim }\limits_{x \to + \infty } (y - ax) = \mathop {\lim }\limits_{x \to + \infty } (\frac{{2{x^2} - 3x}}{{x + 5}} - 2x) = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - 13x}}{{x + 5}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - 13}}{{1 + \frac{5}{x}}} = - 13\)
Ta có: \(\mathop {\lim }\limits_{x \to + \infty } [y - (ax + b)] = \mathop {\lim }\limits_{x \to + \infty } [y - (2x - 3)] = \mathop {\lim }\limits_{x \to + \infty } \frac{{2{x^2} - 3x}}{{x + 5}} - (2x - 13) = \mathop {\lim }\limits_{x \to + \infty } \frac{{65}}{{x + 5}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{\frac{{65}}{x}}}{{1 + \frac{5}{x}}} = 0\)
Do đó, đồ thị hàm số có tiệm cận xiên là đường thẳng y = 2x - 13
Trả lời câu hỏi Thực hành 4 trang 24 SGK Toán 12 Chân trời sáng tạo
Nếu trong một ngày, một xưởng sản xuất được x kilôgam sản phẩm thì chi phí trung bình (tính bằng nghìn đồng) cho một sản phẩm được cho bởi công thức: \(C(x) = \frac{{50x + 2000}}{x}\)
Tìm các đường tiệm cận của hàm số C(x).
Phương pháp giải:
- Đường thẳng x = a được gọi là một đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau thoả mãn: \(\mathop {\lim f(x) = }\limits_{x \to {a^ - }} + \infty ,\mathop {\lim f(x) = }\limits_{x \to {a^ + }} + \infty ,\mathop {\lim f(x) = }\limits_{x \to {a^ - }} - \infty ,\mathop {\lim f(x) = }\limits_{x \to {a^ + }} - \infty \)
- Đường thẳng y = m được gọi là một đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số y = f(x) nếu \(\mathop {\lim }\limits_{x \to - \infty } f(x) = m\) hoặc \(\mathop {\lim }\limits_{x \to + \infty } f(x) = m\)
- Đường thẳng y = ax + b, a ≠ 0, được gọi là đường tiệm cận xiên (hay tiệm cận xiên) của đồ thị hàm số y = f(x) nếu \(\mathop {\lim }\limits_{x \to - \infty } [f(x) - (ax + b)] = 0\) hoặc \(\mathop {\lim }\limits_{x \to + \infty } [f(x) - (ax + b)] = 0\)
Lời giải chi tiết:
Tập xác định: \(D = \mathbb{R}\backslash \left\{ 0 \right\}\)
\(\mathop {\lim }\limits_{x \to {0^ + }} C(x) = \mathop {\lim }\limits_{x \to {0^ + }} \frac{{50x + 2000}}{x} = \frac{{2000}}{0} = + \infty \); \(\mathop {\lim }\limits_{x \to {0^ - }} C(x) = \mathop {\lim }\limits_{x \to {0^ - }} \frac{{50x + 2000}}{x} = \frac{{2000}}{0} = + \infty \)
Vậy tiệm cận đứng của đồ thị hàm số là đường thẳng x = 0
\(\mathop {\lim }\limits_{x \to + \infty } C(x) = \mathop {\lim }\limits_{x \to + \infty } \frac{{50x + 2000}}{x} = \mathop {\lim }\limits_{x \to + \infty } \frac{{50 + \frac{{2000}}{x}}}{1} = 50\); \(\mathop {\lim }\limits_{x \to - \infty } C(x) = \mathop {\lim }\limits_{x \to - \infty } \frac{{50x + 2000}}{x} = \mathop {\lim }\limits_{x \to - \infty } \frac{{50 + \frac{{2000}}{x}}}{1} = 50\)
Vậy tiệm cận ngang của đồ thị hàm số là đường thẳng y = 50
Trả lời câu hỏi Khám phá 3 trang 22 SGK Toán 12 Chân trời sáng tạo
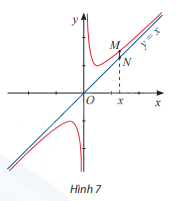
Cho đồ thị của hàm số \(y = \frac{{{x^2} + 1}}{x}\) và đường thẳng y = x. Đường thẳng vuông góc với trục Ox tại điểm x cắt đồ thị hàm số tại điểm M và cắt đường thẳng y = x tại điểm N (Hình 7).
a) Tính \(\mathop {\lim }\limits_{x \to - \infty } (\frac{{{x^2} + 1}}{x} - x)\) và \(\mathop {\lim }\limits_{x \to + \infty } (\frac{{{x^2} + 1}}{x} - x)\)
b) Tính MN theo x và nhận xét về MN khi \(x \to + \infty \) hoặc \(x \to - \infty \)
Phương pháp giải:
Quan sát đồ thị
Lời giải chi tiết:
a) Tập xác định: \(D = \mathbb{R}\backslash \left\{ 0 \right\}\)
Ta có: \(\mathop {\lim }\limits_{x \to - \infty } (\frac{{{x^2} + 1}}{x} - x) = \mathop {\lim }\limits_{x \to - \infty } \frac{{{x^2} + 1 - {x^2}}}{x} = \mathop {\lim }\limits_{x \to - \infty } \frac{1}{x} = 0\); \(\mathop {\lim }\limits_{x \to + \infty } (\frac{{{x^2} + 1}}{x} - x) = \mathop {\lim }\limits_{x \to + \infty } \frac{{{x^2} + 1 - {x^2}}}{x} = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{x} = 0\)
Do đó, đồ thị hàm số có tiệm cận xiên là đường thẳng y = x
b) MN = y – x = \(\frac{{{x^2} + 1}}{x} - x = \frac{1}{x}\)
Khi \(x \to + \infty \) hoặc \(x \to - \infty \) thì MN tiến dần về 0
Trả lời câu hỏi Khám phá 3 trang 22 SGK Toán 12 Chân trời sáng tạo
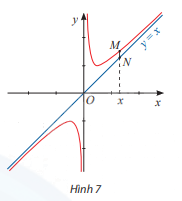
Cho đồ thị của hàm số \(y = \frac{{{x^2} + 1}}{x}\) và đường thẳng y = x. Đường thẳng vuông góc với trục Ox tại điểm x cắt đồ thị hàm số tại điểm M và cắt đường thẳng y = x tại điểm N (Hình 7).
a) Tính \(\mathop {\lim }\limits_{x \to - \infty } (\frac{{{x^2} + 1}}{x} - x)\) và \(\mathop {\lim }\limits_{x \to + \infty } (\frac{{{x^2} + 1}}{x} - x)\)
b) Tính MN theo x và nhận xét về MN khi \(x \to + \infty \) hoặc \(x \to - \infty \)
Phương pháp giải:
Quan sát đồ thị
Lời giải chi tiết:
a) Tập xác định: \(D = \mathbb{R}\backslash \left\{ 0 \right\}\)
Ta có: \(\mathop {\lim }\limits_{x \to - \infty } (\frac{{{x^2} + 1}}{x} - x) = \mathop {\lim }\limits_{x \to - \infty } \frac{{{x^2} + 1 - {x^2}}}{x} = \mathop {\lim }\limits_{x \to - \infty } \frac{1}{x} = 0\); \(\mathop {\lim }\limits_{x \to + \infty } (\frac{{{x^2} + 1}}{x} - x) = \mathop {\lim }\limits_{x \to + \infty } \frac{{{x^2} + 1 - {x^2}}}{x} = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{x} = 0\)
Do đó, đồ thị hàm số có tiệm cận xiên là đường thẳng y = x
b) MN = y – x = \(\frac{{{x^2} + 1}}{x} - x = \frac{1}{x}\)
Khi \(x \to + \infty \) hoặc \(x \to - \infty \) thì MN tiến dần về 0
Trả lời câu hỏi Thực hành 3 trang 24 SGK Toán 12 Chân trời sáng tạo
Tìm tiệm cận xiên của đồ thị hàm số \(y = \frac{{2{x^2} - 3x}}{{x + 5}}\)
Phương pháp giải:
Đường thẳng y = ax + b, a ≠ 0, được gọi là đường tiệm cận xiên (hay tiệm cận xiên) của đồ thị hàm số y = f(x) nếu \(\mathop {\lim }\limits_{x \to - \infty } [f(x) - (ax + b)] = 0\) hoặc \(\mathop {\lim }\limits_{x \to + \infty } [f(x) - (ax + b)] = 0\)
Lời giải chi tiết:
Tập xác định: \(D = \mathbb{R}\backslash \left\{ { - 5} \right\}\)
Ta có: \(a = \mathop {\lim }\limits_{x \to + \infty } \frac{y}{x} = \mathop {\lim }\limits_{x \to + \infty } \frac{{\frac{{2{x^2} - 3x}}{{x + 5}}}}{x} = \mathop {\lim }\limits_{x \to + \infty } \frac{{2{x^2} - 3x}}{{{x^2} + 5x}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{2 - \frac{3}{x}}}{{1 + \frac{5}{x}}} = 2\)
\(b = \mathop {\lim }\limits_{x \to + \infty } (y - ax) = \mathop {\lim }\limits_{x \to + \infty } (\frac{{2{x^2} - 3x}}{{x + 5}} - 2x) = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - 13x}}{{x + 5}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - 13}}{{1 + \frac{5}{x}}} = - 13\)
Ta có: \(\mathop {\lim }\limits_{x \to + \infty } [y - (ax + b)] = \mathop {\lim }\limits_{x \to + \infty } [y - (2x - 3)] = \mathop {\lim }\limits_{x \to + \infty } \frac{{2{x^2} - 3x}}{{x + 5}} - (2x - 13) = \mathop {\lim }\limits_{x \to + \infty } \frac{{65}}{{x + 5}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{\frac{{65}}{x}}}{{1 + \frac{5}{x}}} = 0\)
Do đó, đồ thị hàm số có tiệm cận xiên là đường thẳng y = 2x - 13
Trả lời câu hỏi Thực hành 4 trang 24 SGK Toán 12 Chân trời sáng tạo
Nếu trong một ngày, một xưởng sản xuất được x kilôgam sản phẩm thì chi phí trung bình (tính bằng nghìn đồng) cho một sản phẩm được cho bởi công thức: \(C(x) = \frac{{50x + 2000}}{x}\)
Tìm các đường tiệm cận của hàm số C(x).
Phương pháp giải:
- Đường thẳng x = a được gọi là một đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau thoả mãn: \(\mathop {\lim f(x) = }\limits_{x \to {a^ - }} + \infty ,\mathop {\lim f(x) = }\limits_{x \to {a^ + }} + \infty ,\mathop {\lim f(x) = }\limits_{x \to {a^ - }} - \infty ,\mathop {\lim f(x) = }\limits_{x \to {a^ + }} - \infty \)
- Đường thẳng y = m được gọi là một đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số y = f(x) nếu \(\mathop {\lim }\limits_{x \to - \infty } f(x) = m\) hoặc \(\mathop {\lim }\limits_{x \to + \infty } f(x) = m\)
- Đường thẳng y = ax + b, a ≠ 0, được gọi là đường tiệm cận xiên (hay tiệm cận xiên) của đồ thị hàm số y = f(x) nếu \(\mathop {\lim }\limits_{x \to - \infty } [f(x) - (ax + b)] = 0\) hoặc \(\mathop {\lim }\limits_{x \to + \infty } [f(x) - (ax + b)] = 0\)
Lời giải chi tiết:
Tập xác định: \(D = \mathbb{R}\backslash \left\{ 0 \right\}\)
\(\mathop {\lim }\limits_{x \to {0^ + }} C(x) = \mathop {\lim }\limits_{x \to {0^ + }} \frac{{50x + 2000}}{x} = \frac{{2000}}{0} = + \infty \); \(\mathop {\lim }\limits_{x \to {0^ - }} C(x) = \mathop {\lim }\limits_{x \to {0^ - }} \frac{{50x + 2000}}{x} = \frac{{2000}}{0} = + \infty \)
Vậy tiệm cận đứng của đồ thị hàm số là đường thẳng x = 0
\(\mathop {\lim }\limits_{x \to + \infty } C(x) = \mathop {\lim }\limits_{x \to + \infty } \frac{{50x + 2000}}{x} = \mathop {\lim }\limits_{x \to + \infty } \frac{{50 + \frac{{2000}}{x}}}{1} = 50\); \(\mathop {\lim }\limits_{x \to - \infty } C(x) = \mathop {\lim }\limits_{x \to - \infty } \frac{{50x + 2000}}{x} = \mathop {\lim }\limits_{x \to - \infty } \frac{{50 + \frac{{2000}}{x}}}{1} = 50\)
Vậy tiệm cận ngang của đồ thị hàm số là đường thẳng y = 50
Mục 3 trong SGK Toán 12 tập 1 chương trình Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết các bài tập trong mục này một cách hiệu quả, học sinh cần nắm vững kiến thức lý thuyết, các định nghĩa, định lý và công thức liên quan. Ngoài ra, việc luyện tập thường xuyên với các bài tập tương tự cũng rất quan trọng.
Để hiểu rõ hơn về nội dung Mục 3, chúng ta cần xem xét chi tiết các bài tập và kiến thức được đề cập trong SGK. Thông thường, mục này sẽ bao gồm các dạng bài tập sau:
Bài 1: (Nêu lại đề bài). Lời giải: (Giải chi tiết từng bước, kèm theo giải thích rõ ràng). Ví dụ: Để giải bài tập này, ta sử dụng định lý... và áp dụng công thức... Kết quả: ...
Bài 2: (Nêu lại đề bài). Lời giải: (Giải chi tiết từng bước, kèm theo giải thích rõ ràng). Ví dụ: Ta cần phân tích bài toán thành các bước nhỏ hơn. Bước 1: ... Bước 2: ... Kết quả: ...
Bài 3: (Nêu lại đề bài). Lời giải: (Giải chi tiết từng bước, kèm theo giải thích rõ ràng). Ví dụ: Bài toán này đòi hỏi sự hiểu biết về... Kết quả: ...
Bài 4: (Nêu lại đề bài). Lời giải: (Giải chi tiết từng bước, kèm theo giải thích rõ ràng). Ví dụ: Ta có thể sử dụng phương pháp... để giải quyết bài toán này. Kết quả: ...
Bài 5: (Nêu lại đề bài). Lời giải: (Giải chi tiết từng bước, kèm theo giải thích rõ ràng). Ví dụ: Bài toán này liên quan đến... Kết quả: ...
Bài 6: (Nêu lại đề bài). Lời giải: (Giải chi tiết từng bước, kèm theo giải thích rõ ràng). Ví dụ: Ta cần chú ý đến các điều kiện của bài toán. Kết quả: ...
Để giải các bài tập Toán 12 tập 1 chương trình Chân trời sáng tạo một cách nhanh chóng và hiệu quả, các em có thể áp dụng một số mẹo sau:
Kiến thức được học trong Mục 3 có ứng dụng rất lớn trong việc giải quyết các bài toán thực tế và trong các kỳ thi quan trọng. Việc nắm vững kiến thức này sẽ giúp các em tự tin hơn khi đối mặt với các bài toán khó.
Ngoài SGK, các em có thể tham khảo thêm các tài liệu sau để nâng cao kiến thức:
Hy vọng rằng với lời giải chi tiết và những hướng dẫn trên, các em học sinh sẽ giải quyết thành công các bài tập trong Mục 3 trang 22, 23, 24 SGK Toán 12 tập 1 chương trình Chân trời sáng tạo. Chúc các em học tập tốt!