Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập Toán 12 tập 1 - Chân trời sáng tạo. Bài viết này sẽ giúp bạn hiểu rõ cách giải bài tập 3 trang 13, từ đó nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, giúp bạn tiết kiệm thời gian và đạt kết quả tốt nhất.
Tìm cực trị của các hàm số sau: a) (y = 2{x^3} + 3{x^2}--36x + 1) b) (y = frac{{{x^2} - 8x + 10}}{{x - 2}}) c) (y = sqrt { - {x^2} + 4} )
Đề bài
Tìm cực trị của các hàm số sau:a) \(y = 2{x^3} + 3{x^2}--36x + 1\)b) \(y = \frac{{{x^2} - 8x + 10}}{{x - 2}}\)c) \(y = \sqrt { - {x^2} + 4} \)
Phương pháp giải - Xem chi tiết
Tìm tập xác định, đạo hàm và lập bảng biến thiên
Lời giải chi tiết
a) \(y = 2{x^3} + 3{x^2}--36x + 1\)
Tập xác định: \(D = \mathbb{R}\)
\(y' = 6{x^2} + 6x - 36\)
\(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = - 3\end{array} \right.\)
Bảng biến thiên:
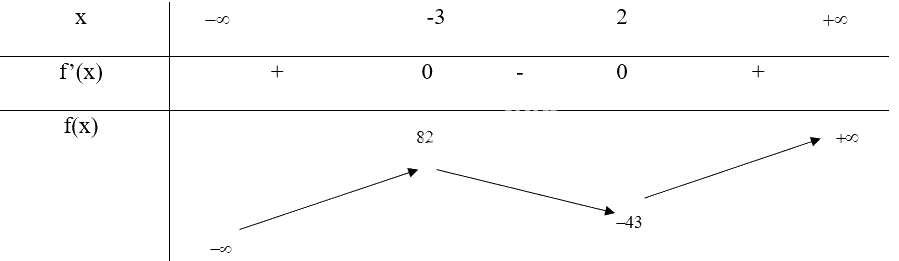
Hàm số đạt cực đại tại x = -3, \({y_{cd}} = f( - 3) = 82\), đạt cực tiểu tại x = 2, \({y_{ct}} = f(2) = - 43\)
b) \(y = \frac{{{x^2} - 8x + 10}}{{x - 2}}\)
Tập xác định: \(D = \mathbb{R}\backslash \{ 2\} \)
\(y' = \frac{{{x^2} - 4x + 6}}{{{{(x - 2)}^2}}}\)
Ta có: \(\left\{ \begin{array}{l}({x^2} - 4x + 6) > 0\forall x \in \mathbb{R}\backslash \{ 2\} \\{(x - 2)^2} > 0\forall x \in \mathbb{R}\backslash \{ 2\} \end{array} \right.\) nên \(y' > 0\forall x \in \mathbb{R}\backslash \{ 2\} \)
Bảng biến thiên:
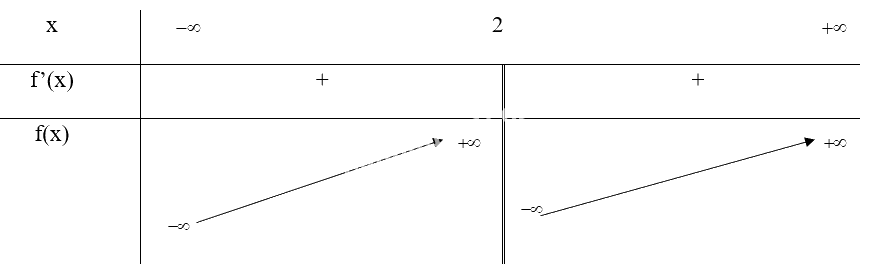
Vậy hàm số không có điểm cực trị
c) \(y = \sqrt { - {x^2} + 4} \)
Tập xác định: \(D = \left( { - 2;2} \right)\)
\(y' = \frac{{ - x}}{{\sqrt { - {x^2} + 4} }}\)
\(y' = 0 \Leftrightarrow x = 0\)
Bảng biến thiên:
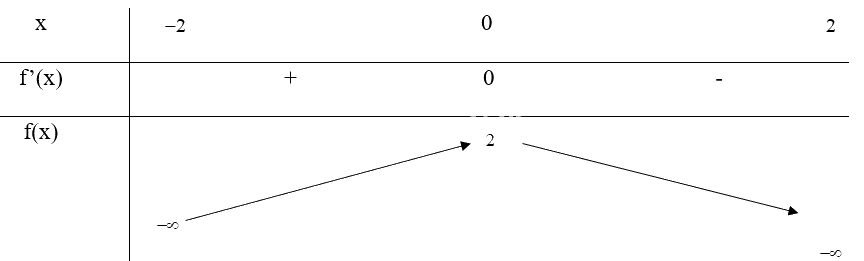
Hàm số đạt cực đại tại x = 0, \({y_{cd}} = f(0) = 2\)
Bài tập 3 trang 13 SGK Toán 12 tập 1 - Chân trời sáng tạo thuộc chương trình học về giới hạn của hàm số. Đây là một phần kiến thức quan trọng, nền tảng cho các chương trình học toán cao hơn. Việc nắm vững các khái niệm và phương pháp giải bài tập trong chương này sẽ giúp học sinh xây dựng một nền tảng toán học vững chắc.
Bài tập 3 trang 13 SGK Toán 12 tập 1 - Chân trời sáng tạo thường bao gồm các dạng bài tập sau:
Để giải bài tập 3 trang 13 SGK Toán 12 tập 1 - Chân trời sáng tạo hiệu quả, học sinh cần nắm vững các phương pháp sau:
Ví dụ 1: Tính giới hạn limx→2 (x2 - 4) / (x - 2)
Giải:
Ta có: limx→2 (x2 - 4) / (x - 2) = limx→2 (x - 2)(x + 2) / (x - 2) = limx→2 (x + 2) = 4
Để củng cố kiến thức và kỹ năng giải bài tập về giới hạn, học sinh nên luyện tập thêm với các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Ngoài ra, việc tham gia các diễn đàn học tập trực tuyến hoặc tìm kiếm sự giúp đỡ từ giáo viên và bạn bè cũng là những cách hiệu quả để nâng cao khả năng giải toán.
Khi giải bài tập về giới hạn, học sinh cần chú ý đến các điểm sau:
Bài tập 3 trang 13 SGK Toán 12 tập 1 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh hiểu rõ hơn về khái niệm giới hạn và các phương pháp tính giới hạn. Việc nắm vững kiến thức và kỹ năng giải bài tập này sẽ giúp học sinh tự tin hơn trong quá trình học tập môn Toán.