Chào mừng các em học sinh đến với lời giải chi tiết bài tập 10 trang 65 SGK Toán 12 tập 1 - Chân trời sáng tạo. Bài viết này được giaitoan.edu.vn biên soạn nhằm hỗ trợ các em trong quá trình ôn tập và làm bài tập Toán 12 hiệu quả.
Chúng tôi cung cấp lời giải đầy đủ, dễ hiểu, kèm theo các bước giải chi tiết và phân tích chuyên sâu, giúp các em nắm vững kiến thức và kỹ năng giải toán.
Tìm toạ độ của điểm P được biểu diễn trong Hình 2 và tính khoảng cách OP.
Đề bài
Tìm toạ độ của điểm P được biểu diễn trong Hình 2 và tính khoảng cách OP.
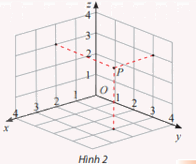
Phương pháp giải - Xem chi tiết
Quan sát hình vẽ và xem hình chiếu của P lên các mặt phẳng có tọa độ là bao nhiêu => tọa độ của P. Công thức tính độ lớn vecto: \(|\overrightarrow a | = \sqrt {{a_1}^2 + {a_2}^2 + {a_3}^2} \)
Lời giải chi tiết
P(2;3;3) => \(\overrightarrow {OP} = (2;3;3) \Rightarrow OP = \sqrt {{2^2} + {3^2} + {3^2}} = \sqrt {22} \)
Bài tập 10 trang 65 SGK Toán 12 tập 1 - Chân trời sáng tạo thuộc chương trình học về đạo hàm. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán thực tế. Việc nắm vững các khái niệm và công thức đạo hàm là yếu tố then chốt để hoàn thành tốt bài tập này.
Bài tập 10 bao gồm các câu hỏi liên quan đến việc tính đạo hàm của hàm số, tìm điểm cực trị của hàm số và khảo sát hàm số. Cụ thể, bài tập yêu cầu học sinh:
Để giải quyết bài tập 10 trang 65 SGK Toán 12 tập 1 - Chân trời sáng tạo, học sinh cần nắm vững các phương pháp sau:
Dưới đây là lời giải chi tiết cho từng câu hỏi trong bài tập 10 trang 65 SGK Toán 12 tập 1 - Chân trời sáng tạo:
Đề bài: Tính đạo hàm của hàm số f(x) = x3 - 3x2 + 2x - 1.
Lời giải:
f'(x) = 3x2 - 6x + 2
Đề bài: Tìm các điểm cực trị của hàm số g(x) = x4 - 4x2 + 3.
Lời giải:
g'(x) = 4x3 - 8x
Giải phương trình g'(x) = 0, ta được x = 0, x = √2, x = -√2.
Vậy hàm số g(x) có các điểm cực trị tại x = 0, x = √2, x = -√2.
Đề bài: Khảo sát sự biến thiên của hàm số h(x) = x2 - 2x + 1.
Lời giải:
h'(x) = 2x - 2
Giải phương trình h'(x) = 0, ta được x = 1.
Hàm số h(x) đồng biến trên khoảng (1, +∞) và nghịch biến trên khoảng (-∞, 1).
Bài tập 10 trang 65 SGK Toán 12 tập 1 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm. Hy vọng với lời giải chi tiết và phương pháp giải được trình bày trong bài viết này, các em sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn Toán 12.