Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 2 trang 33, 34 SGK Toán 12 tập 2 chương trình Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập một cách khoa học và hiệu quả.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, tự tin giải quyết các bài toán Toán 12 và đạt kết quả cao trong học tập.
Trong không gian (Oxyz), cho mặt phẳng (left( alpha right)) có cặp vectơ chỉ phương (vec a = left( {{a_1};{a_2};{a_3}} right)), (vec b = left( {{b_1};{b_2};{b_3}} right)). Xét vectơ (vec n = left( {{a_2}{b_3} - {a_3}{b_2};{a_3}{b_1} - {a_1}{b_3};{a_1}{b_2} - {a_2}{b_1}} right)).
Trả lời câu hỏi Hoạt động 2 trang 33, 34 SGK Toán 12 Chân trời sáng tạo
Trong không gian \(Oxyz\), cho mặt phẳng \(\left( \alpha \right)\) có cặp vectơ chỉ phương \(\vec a = \left( {{a_1};{a_2};{a_3}} \right)\), \(\vec b = \left( {{b_1};{b_2};{b_3}} \right)\). Xét vectơ \(\vec n = \left( {{a_2}{b_3} - {a_3}{b_2};{a_3}{b_1} - {a_1}{b_3};{a_1}{b_2} - {a_2}{b_1}} \right)\).
a) Vectơ \(\vec n\) có khác \(\vec 0\) hay không?
b) Tính \(\vec a.\vec n\); \(\vec b.\vec n\).
c) Vectơ \(\vec n\) có phải là vectơ pháp tuyến của mặt phẳng \(\left( \alpha \right)\) không?
Phương pháp giải:
a) Giả sử \(\vec n = \vec 0\), sau đó chứng minh rằng \(\vec a\) và \(\vec b\) là hai vectơ cùng phương. Điều này là vô lí do \(\vec a\) và \(\vec b\) là một cặp vectơ chỉ phương của \(\left( \alpha \right)\).
b) Sử dụng công thức tích vô hướng của hai vectơ trong không gian.
c) Để chứng minh \(\vec n\) là vectơ pháp tuyến của mặt phẳng \(\left( \alpha \right)\), ta chỉ ra rằng \(\vec n\) có giá vuông góc với mặt phẳng \(\left( \alpha \right)\).
Lời giải chi tiết:
a) Giả sử \(\vec n = \vec 0\), khi đó \({a_2}{b_3} - {a_3}{b_2} = {a_3}{b_1} - {a_1}{b_3} = {a_1}{b_2} - {a_2}{b_1} = 0\).
Với trường hợp \({b_1}\), \({b_2}\), \({b_3}\) cùng khác 0, ta suy ra \(\frac{{{a_1}}}{{{b_1}}} = \frac{{{a_2}}}{{{b_2}}} = \frac{{{a_3}}}{{{b_3}}}\), điều này có nghĩa \(\vec a\) và \(\vec b\) là hai vectơ cùng phương.
Nếu \({b_1} = 0\) thì \({a_1} = 0\), ta vẫn thu được kết quả \(\vec a\) và \(\vec b\) là hai vectơ cùng phương.
Các trường hợp còn lại cho ra kết quả tương tự.
Như vậy \(\vec a\) và \(\vec b\) là hai vectơ cùng phương.
Mặt khác, do \(\vec a\) và \(\vec b\) là một cặp vectơ chỉ phương của \(\left( \alpha \right)\), nên \(\vec a\) và \(\vec b\) là hai vectơ không cùng phương, mâu thuẫn.
Như vậy \(\vec n \ne \vec 0\).
b) Ta có:
+)\(\vec a.\vec n = {a_1}\left( {{a_2}{b_3} - {a_3}{b_2}} \right) + {a_2}\left( {{a_3}{b_1} - {a_1}{b_3}} \right) + {a_3}\left( {{a_1}{b_2} - {a_2}{b_1}} \right)\)
\( = {a_1}{a_2}{b_3} - {a_1}{a_3}{b_2} + {a_2}{a_3}{b_1} - {a_2}{a_1}{b_3} + {a_3}{a_1}{b_2} - {a_3}{a_2}{b_1} = 0\)
+) \(\vec b.\vec n = {b_1}\left( {{a_2}{b_3} - {a_3}{b_2}} \right) + {b_2}\left( {{a_3}{b_1} - {a_1}{b_3}} \right) + {b_3}\left( {{a_1}{b_2} - {a_2}{b_1}} \right)\)
\( = {b_1}{a_2}{b_3} - {b_1}{a_3}{b_2} + {b_2}{a_3}{b_1} - {b_2}{a_1}{b_3} + {b_3}{a_1}{b_2} - {b_3}{a_2}{b_1} = 0\)
Như vậy \(\vec a.\vec n = \vec b.\vec n = 0\).
c) Theo câu b, ta có \(\vec a.\vec n = \vec b.\vec n = 0\), điều này có nghĩa là \(\vec n\) có giá vuông góc với giá của \(\vec a\) và \(\vec b\). Mà \(\vec a\) và \(\vec b\) là một cặp vectơ chỉ phương của \(\left( \alpha \right)\), nên \(\vec n\) có giá vuông góc với mặt phẳng \(\left( \alpha \right)\). Như vậy \(\vec n\) là một vectơ pháp tuyến của \(\left( \alpha \right)\).
Trả lời câu hỏi Thực hành 2 trang 34 SGK Toán 12 Chân trời sáng tạo
Cho mặt phẳng \(\left( Q \right)\) đi qua ba điểm \(A\left( {1;1;1} \right)\), \(B\left( { - 1;1;5} \right)\), \(C\left( {10;7; - 1} \right)\). Tìm một cặp vectơ chỉ phương và một vectơ pháp tuyến của \(\left( Q \right)\).
Phương pháp giải:
Mặt phẳng \(\left( Q \right)\) đi qua \(A\left( {1;1;1} \right)\), \(B\left( { - 1;1;5} \right)\), , nên nó sẽ có một cặp vectơ chỉ phương là và .
Để tìm toạ độ một vectơ pháp tuyến của mặt phẳng , thực hiện tính tích có hướng của hai vectơ và . Vectơ thu được là một\(C\left( {10;7; - 1} \right)\) vectơ pháp tuyến của \(\left( Q \right)\).
Lời giải chi tiết:
Ta có \(\left( Q \right)\) đi qua \(A\left( {1;1;1} \right)\), \(B\left( { - 1;1;5} \right)\), \(C\left( {10;7; - 1} \right)\), nên nó sẽ có một cặp vectơ chỉ phương là \(\overrightarrow {AB} \left( { - 2;0;4} \right)\) và \(\overrightarrow {AC} \left( {9;6; - 2} \right)\).
Tích có hướng của hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) là:
\(\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {0.\left( { - 2} \right) - 4.6;4.9 - \left( { - 2} \right).\left( { - 2} \right); - 2.6 - 0.9} \right) = \left( { - 24;32; - 12} \right)\)
Do đó, mặt phẳng \(\left( Q \right)\) nhận \(\vec n = \frac{1}{4}\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( { - 6;8; - 3} \right)\) làm một vectơ pháp tuyến.
Trả lời câu hỏi Hoạt động 2 trang 33, 34 SGK Toán 12 Chân trời sáng tạo
Trong không gian \(Oxyz\), cho mặt phẳng \(\left( \alpha \right)\) có cặp vectơ chỉ phương \(\vec a = \left( {{a_1};{a_2};{a_3}} \right)\), \(\vec b = \left( {{b_1};{b_2};{b_3}} \right)\). Xét vectơ \(\vec n = \left( {{a_2}{b_3} - {a_3}{b_2};{a_3}{b_1} - {a_1}{b_3};{a_1}{b_2} - {a_2}{b_1}} \right)\).
a) Vectơ \(\vec n\) có khác \(\vec 0\) hay không?
b) Tính \(\vec a.\vec n\); \(\vec b.\vec n\).
c) Vectơ \(\vec n\) có phải là vectơ pháp tuyến của mặt phẳng \(\left( \alpha \right)\) không?
Phương pháp giải:
a) Giả sử \(\vec n = \vec 0\), sau đó chứng minh rằng \(\vec a\) và \(\vec b\) là hai vectơ cùng phương. Điều này là vô lí do \(\vec a\) và \(\vec b\) là một cặp vectơ chỉ phương của \(\left( \alpha \right)\).
b) Sử dụng công thức tích vô hướng của hai vectơ trong không gian.
c) Để chứng minh \(\vec n\) là vectơ pháp tuyến của mặt phẳng \(\left( \alpha \right)\), ta chỉ ra rằng \(\vec n\) có giá vuông góc với mặt phẳng \(\left( \alpha \right)\).
Lời giải chi tiết:
a) Giả sử \(\vec n = \vec 0\), khi đó \({a_2}{b_3} - {a_3}{b_2} = {a_3}{b_1} - {a_1}{b_3} = {a_1}{b_2} - {a_2}{b_1} = 0\).
Với trường hợp \({b_1}\), \({b_2}\), \({b_3}\) cùng khác 0, ta suy ra \(\frac{{{a_1}}}{{{b_1}}} = \frac{{{a_2}}}{{{b_2}}} = \frac{{{a_3}}}{{{b_3}}}\), điều này có nghĩa \(\vec a\) và \(\vec b\) là hai vectơ cùng phương.
Nếu \({b_1} = 0\) thì \({a_1} = 0\), ta vẫn thu được kết quả \(\vec a\) và \(\vec b\) là hai vectơ cùng phương.
Các trường hợp còn lại cho ra kết quả tương tự.
Như vậy \(\vec a\) và \(\vec b\) là hai vectơ cùng phương.
Mặt khác, do \(\vec a\) và \(\vec b\) là một cặp vectơ chỉ phương của \(\left( \alpha \right)\), nên \(\vec a\) và \(\vec b\) là hai vectơ không cùng phương, mâu thuẫn.
Như vậy \(\vec n \ne \vec 0\).
b) Ta có:
+)\(\vec a.\vec n = {a_1}\left( {{a_2}{b_3} - {a_3}{b_2}} \right) + {a_2}\left( {{a_3}{b_1} - {a_1}{b_3}} \right) + {a_3}\left( {{a_1}{b_2} - {a_2}{b_1}} \right)\)
\( = {a_1}{a_2}{b_3} - {a_1}{a_3}{b_2} + {a_2}{a_3}{b_1} - {a_2}{a_1}{b_3} + {a_3}{a_1}{b_2} - {a_3}{a_2}{b_1} = 0\)
+) \(\vec b.\vec n = {b_1}\left( {{a_2}{b_3} - {a_3}{b_2}} \right) + {b_2}\left( {{a_3}{b_1} - {a_1}{b_3}} \right) + {b_3}\left( {{a_1}{b_2} - {a_2}{b_1}} \right)\)
\( = {b_1}{a_2}{b_3} - {b_1}{a_3}{b_2} + {b_2}{a_3}{b_1} - {b_2}{a_1}{b_3} + {b_3}{a_1}{b_2} - {b_3}{a_2}{b_1} = 0\)
Như vậy \(\vec a.\vec n = \vec b.\vec n = 0\).
c) Theo câu b, ta có \(\vec a.\vec n = \vec b.\vec n = 0\), điều này có nghĩa là \(\vec n\) có giá vuông góc với giá của \(\vec a\) và \(\vec b\). Mà \(\vec a\) và \(\vec b\) là một cặp vectơ chỉ phương của \(\left( \alpha \right)\), nên \(\vec n\) có giá vuông góc với mặt phẳng \(\left( \alpha \right)\). Như vậy \(\vec n\) là một vectơ pháp tuyến của \(\left( \alpha \right)\).
Trả lời câu hỏi Thực hành 2 trang 34 SGK Toán 12 Chân trời sáng tạo
Cho mặt phẳng \(\left( Q \right)\) đi qua ba điểm \(A\left( {1;1;1} \right)\), \(B\left( { - 1;1;5} \right)\), \(C\left( {10;7; - 1} \right)\). Tìm một cặp vectơ chỉ phương và một vectơ pháp tuyến của \(\left( Q \right)\).
Phương pháp giải:
Mặt phẳng \(\left( Q \right)\) đi qua \(A\left( {1;1;1} \right)\), \(B\left( { - 1;1;5} \right)\), , nên nó sẽ có một cặp vectơ chỉ phương là và .
Để tìm toạ độ một vectơ pháp tuyến của mặt phẳng , thực hiện tính tích có hướng của hai vectơ và . Vectơ thu được là một\(C\left( {10;7; - 1} \right)\) vectơ pháp tuyến của \(\left( Q \right)\).
Lời giải chi tiết:
Ta có \(\left( Q \right)\) đi qua \(A\left( {1;1;1} \right)\), \(B\left( { - 1;1;5} \right)\), \(C\left( {10;7; - 1} \right)\), nên nó sẽ có một cặp vectơ chỉ phương là \(\overrightarrow {AB} \left( { - 2;0;4} \right)\) và \(\overrightarrow {AC} \left( {9;6; - 2} \right)\).
Tích có hướng của hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) là:
\(\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {0.\left( { - 2} \right) - 4.6;4.9 - \left( { - 2} \right).\left( { - 2} \right); - 2.6 - 0.9} \right) = \left( { - 24;32; - 12} \right)\)
Do đó, mặt phẳng \(\left( Q \right)\) nhận \(\vec n = \frac{1}{4}\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( { - 6;8; - 3} \right)\) làm một vectơ pháp tuyến.
Trả lời câu hỏi Vận dụng 2 trang 34 SGK Toán 12 Chân trời sáng tạo
Cho biết hai vectơ \(\vec a = \left( {2;1;1} \right)\), \(\vec b = \left( {1; - 2;0} \right)\) có giá lần lượt song song với ngón trỏ và ngón giữa của bàn tay trong hình dưới đây. Tìm vectơ \(\vec n\) có giá song song với ngón cái. (Xem như ba ngón tay nói trên tạo thành 3 đường thẳng đôi một vuông góc).
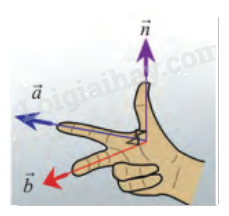
Phương pháp giải:
Theo hình vẽ, do vectơ \(\vec n\) có giá vuông góc lần lượt với giá của hai vectơ \(\vec a\) và \(\vec b\), nên có thể chọn vectơ \(\vec n\) là tích có hướng của hai vectơ \(\vec a\) và \(\vec b\).
Lời giải chi tiết:
Theo hình vẽ, do vectơ \(\vec n\) có giá vuông góc lần lượt với giá của hai vectơ \(\vec a\) và \(\vec b\), nên có thể chọn vectơ \(\vec n\) là tích có hướng của hai vectơ \(\vec a\) và \(\vec b\).
Tích có hướng của hai vectơ \(\vec a\) và \(\vec b\) là
\(\left[ {\vec a,\vec b} \right] = \left( {1.0 - 1.\left( { - 2} \right);1.1 - 2.0;2.\left( { - 2} \right) - 1.1} \right) = \left( {2;1; - 5} \right)\).
Do đó, vectơ \(\vec n\) cần tìm là \(\vec n = \left( {2;1; - 5} \right)\).
Trả lời câu hỏi Vận dụng 2 trang 34 SGK Toán 12 Chân trời sáng tạo
Cho biết hai vectơ \(\vec a = \left( {2;1;1} \right)\), \(\vec b = \left( {1; - 2;0} \right)\) có giá lần lượt song song với ngón trỏ và ngón giữa của bàn tay trong hình dưới đây. Tìm vectơ \(\vec n\) có giá song song với ngón cái. (Xem như ba ngón tay nói trên tạo thành 3 đường thẳng đôi một vuông góc).
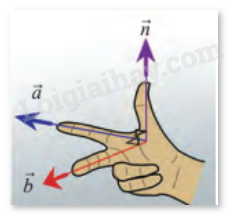
Phương pháp giải:
Theo hình vẽ, do vectơ \(\vec n\) có giá vuông góc lần lượt với giá của hai vectơ \(\vec a\) và \(\vec b\), nên có thể chọn vectơ \(\vec n\) là tích có hướng của hai vectơ \(\vec a\) và \(\vec b\).
Lời giải chi tiết:
Theo hình vẽ, do vectơ \(\vec n\) có giá vuông góc lần lượt với giá của hai vectơ \(\vec a\) và \(\vec b\), nên có thể chọn vectơ \(\vec n\) là tích có hướng của hai vectơ \(\vec a\) và \(\vec b\).
Tích có hướng của hai vectơ \(\vec a\) và \(\vec b\) là
\(\left[ {\vec a,\vec b} \right] = \left( {1.0 - 1.\left( { - 2} \right);1.1 - 2.0;2.\left( { - 2} \right) - 1.1} \right) = \left( {2;1; - 5} \right)\).
Do đó, vectơ \(\vec n\) cần tìm là \(\vec n = \left( {2;1; - 5} \right)\).
Mục 2 của SGK Toán 12 tập 2 chương trình Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể trong chương trình học. Việc nắm vững kiến thức nền tảng và phương pháp giải bài tập là yếu tố then chốt để giải quyết các bài toán một cách hiệu quả. Bài viết này sẽ cung cấp lời giải chi tiết cho từng bài tập trong mục 2 trang 33, 34, đồng thời phân tích các phương pháp giải và lưu ý quan trọng.
Đề bài: (Nêu rõ đề bài)
Lời giải: (Giải thích chi tiết từng bước giải, sử dụng công thức và định lý liên quan. Có thể sử dụng hình ảnh minh họa nếu cần thiết.)
Lưu ý: (Nêu các điểm cần lưu ý khi giải bài tập này, các lỗi thường gặp và cách khắc phục.)
Đề bài: (Nêu rõ đề bài)
Lời giải: (Giải thích chi tiết từng bước giải, sử dụng công thức và định lý liên quan. Có thể sử dụng hình ảnh minh họa nếu cần thiết.)
Lưu ý: (Nêu các điểm cần lưu ý khi giải bài tập này, các lỗi thường gặp và cách khắc phục.)
Đề bài: (Nêu rõ đề bài)
Lời giải: (Giải thích chi tiết từng bước giải, sử dụng công thức và định lý liên quan. Có thể sử dụng hình ảnh minh họa nếu cần thiết.)
Lưu ý: (Nêu các điểm cần lưu ý khi giải bài tập này, các lỗi thường gặp và cách khắc phục.)
Kiến thức trong mục 2 có ứng dụng rộng rãi trong nhiều lĩnh vực của toán học và thực tế. Ví dụ, kiến thức về phương trình và bất phương trình được sử dụng trong việc giải quyết các bài toán tối ưu hóa, mô hình hóa các hiện tượng vật lý và kinh tế. Kiến thức về hàm số được sử dụng trong việc phân tích và dự đoán xu hướng của các hiện tượng tự nhiên và xã hội.
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, các em có thể tham khảo các bài tập luyện tập sau:
Hy vọng rằng bài viết này đã cung cấp cho các em những kiến thức và kỹ năng cần thiết để giải quyết các bài tập trong mục 2 trang 33, 34 SGK Toán 12 tập 2 chương trình Chân trời sáng tạo. Chúc các em học tập tốt và đạt kết quả cao!
| Bài tập | Lời giải |
|---|---|
| Bài 1 | (Link đến lời giải chi tiết) |
| Bài 2 | (Link đến lời giải chi tiết) |