Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12 tập 1 - Chân trời sáng tạo. Bài tập 16 trang 37 là một phần quan trọng trong chương trình học, đòi hỏi học sinh phải nắm vững kiến thức về các khái niệm và phương pháp giải toán đã được học.
Chúng tôi hiểu rằng việc tự giải bài tập đôi khi gặp khó khăn, vì vậy chúng tôi đã biên soạn lời giải chi tiết, kèm theo các bước giải rõ ràng, giúp bạn hiểu rõ bản chất của bài toán và áp dụng vào các bài tập tương tự.
Điện trở R (\(\Omega \)) của một đoạn dây dẫn hình trụ được làm từ vật liệu có điện trở suất \(\rho \)(\(\Omega \)m), chiều dài \(\ell \)(m) và tiết diện S (\({m^2}\)) được cho bởi công thức \(R = \rho \frac{\ell }{S}\) (Vật lí 11 – Chân trời sáng tạo, Nhà xuất bản Giáo dục Việt Nam, 2023, trang 104) Giả sử người ta khảo sát sự biến thiên của điện trở R theo tiết diện S (ở nhiệt độ \(20^\circ C\)) của một sợi dây điện dài 10m làm từ kim loại có điện trở suất \(\rho \) và thu được đồ thị hàm
Đề bài
Điện trở R (\(\Omega \)) của một đoạn dây dẫn hình trụ được làm từ vật liệu có điện trở suất \(\rho \)(\(\Omega \)m), chiều dài \(\ell \)(m) và tiết diện S (\({m^2}\)) được cho bởi công thức
\(R = \rho \frac{\ell }{S}\)
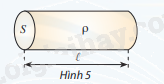
(Vật lí 11 – Chân trời sáng tạo, Nhà xuất bản Giáo dục Việt Nam, 2023, trang 104)
Giả sử người ta khảo sát sự biến thiên của điện trở R theo tiết diện S (ở nhiệt độ \(20^\circ C\)) của một sợi dây điện dài 10m làm từ kim loại có điện trở suất \(\rho \) và thu được đồ thị hàm số như Hình 6.
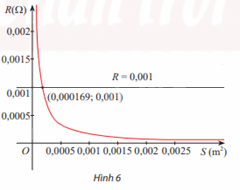
a) Có nhận xét gì về sự biến thiên của điện trở R theo tiết diện S?
b) Từ đồ thị, hãy giải thích ý nghĩa của toạ độ giao điểm của đồ thị hàm số với đường thẳng R = 0,001.
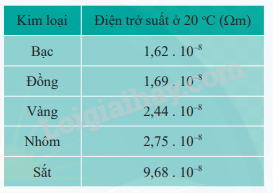
c) Tính điện trở suất \(\rho \) của dây điện. Từ đó, hãy cho biết dây điện được làm bằng kim loại nào trong số các kim loại được cho ở bảng sau:
Phương pháp giải - Xem chi tiết
a) Quan sát đồ thị
b) Giao điểm của đồ thị hàm số với đường thẳng y = a cho biết tại \({x_0}\) thì \({y_0} = a\)
c) Tính \(\rho \) từ công thức của R rồi tra bảng
Lời giải chi tiết
a) Khi \(S \to + \infty \) thì \(R \to 0\), nghĩa là khi S càng lớn thì R càng bé
b) Toạ độ giao điểm của đồ thị hàm số với đường thẳng R = 0,001 cho biết khi S = 0,000169\({m^2}\) thì R = 0,001
c) \(\rho = \frac{{RS}}{\ell } = \frac{{0,001.0,000169}}{{10}} = 1,{69.10^{ - 8}}(\Omega m)\)
Vậy dây điện trở được làm bằng đồng
Bài tập 16 trang 37 SGK Toán 12 tập 1 - Chân trời sáng tạo thuộc chương trình học về giới hạn của hàm số. Để giải quyết bài tập này, học sinh cần nắm vững các khái niệm về giới hạn một bên, giới hạn tại một điểm, và các tính chất của giới hạn.
Trước khi bắt đầu giải bài tập, điều quan trọng là phải đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Bài tập 16 thường yêu cầu học sinh tính giới hạn của một hàm số tại một điểm cho trước, hoặc chứng minh một giới hạn nào đó.
Giả sử bài tập 16 yêu cầu tính giới hạn của hàm số f(x) = (x^2 - 1) / (x - 1) khi x tiến tới 1.
Giải:
Ta có thể phân tích tử số thành nhân tử: x^2 - 1 = (x - 1)(x + 1).
Vậy, f(x) = (x - 1)(x + 1) / (x - 1) = x + 1 (với x ≠ 1).
Khi x tiến tới 1, f(x) tiến tới 1 + 1 = 2.
Vậy, lim (x→1) f(x) = 2.
Kiến thức về giới hạn có ứng dụng rộng rãi trong nhiều lĩnh vực của toán học, như giải tích, hình học, và xác suất thống kê. Nó cũng là nền tảng để hiểu các khái niệm phức tạp hơn, như đạo hàm và tích phân.
Ngoài SGK Toán 12 tập 1 - Chân trời sáng tạo, bạn có thể tham khảo thêm các tài liệu sau để học tập và ôn luyện:
Giaitoan.edu.vn hy vọng rằng với hướng dẫn chi tiết này, bạn sẽ tự tin giải quyết bài tập 16 trang 37 SGK Toán 12 tập 1 - Chân trời sáng tạo và đạt kết quả tốt trong môn Toán.