Lý thuyết Biểu thức tọa độ của các phép toán vecto Toán 12 Chân trời sáng tạo

Chào mừng bạn đến với bài học lý thuyết về biểu thức tọa độ của các phép toán vecto trong chương trình Toán 12 Chân trời sáng tạo.

Bài học này sẽ cung cấp cho bạn những kiến thức nền tảng và công thức quan trọng để giải quyết các bài toán liên quan đến vecto trong không gian, đặc biệt là các phép toán cộng, trừ, nhân với một số và các tích vô hướng, tích có hướng.

Bài 3. Biểu thức tọa độ của các phép toán vecto 1. Biểu thức tọa độ của tổng, hiệu hai vecto và tích của một số với một vecto

1. Biểu thức tọa độ của tổng, hiệu hai vecto và tích của một số với một vecto

Trong không gian Oxyz, cho hai vecto \(\overrightarrow a = (x;y;z)\) và \(\overrightarrow b = (x';y';z')\). Ta có:

\(\overrightarrow a + \overrightarrow b = (x + x';y + y';z + z')\)
\(\overrightarrow a - \overrightarrow b = (x - x';y - y';z - z')\)
\(k\overrightarrow a = (kx;ky;kz)\) với k là một số thực

2. Biểu thức tọa độ của tích vô hướng

Trong không gian Oxyz, tích vô hướng của hai vecto \(\overrightarrow a = (x;y;z)\) và \(\overrightarrow b = (x';y';z')\) được xác định bởi công thức \(\overrightarrow a \cdot \overrightarrow b = xx' + yy' + zz'\)

3. Vận dụng

a) Xác định tọa độ của vecto khi biết tọa độ điểm đầu và điểm cuối

Trong không gian Oxyz, cho hai điểm \(A({x_A};{y_A};{z_A}),B({x_B};{y_B};{z_B})\). Ta có:

\(\overrightarrow {AB} = ({x_B} - {x_A};{y_B} - {y_A};{z_B} - {z_A})\)

b) Tọa độ trung điểm đoạn thẳng. Tọa độ trọng tâm tam giác

Trong không gian Oxyz, cho ba điểm không thẳng hàng \(A({x_A};{y_A};{z_A}),B({x_B};{y_B};{z_B}),C({x_C};{y_C};{z_C})\). Khi đó:

Tọa độ trung điểm của đoạn thẳng AB là \(\left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2};\frac{{{z_A} + {z_B}}}{2}} \right)\)
Tọa độ trọng tâm tam giác ABC là \(\left( {\frac{{{x_A} + {x_B} + {x_C}}}{2};\frac{{{y_A} + {y_B} + {y_C}}}{2};\frac{{{z_A} + {z_B} + {z_C}}}{2}} \right)\)

Tự tin bứt phá Kỳ thi THPT Quốc gia môn Toán! Đừng bỏ lỡ Lý thuyết Biểu thức tọa độ của các phép toán vecto Toán 12 Chân trời sáng tạo đặc sắc thuộc chuyên mục toán lớp 12 trên nền tảng toán học. Với bộ bài tập toán thpt được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình Toán 12, đây chính là "chiến lược vàng" giúp các em tối ưu hóa ôn luyện. Học sinh sẽ không chỉ làm chủ mọi dạng bài thi mà còn nắm vững chiến thuật làm bài hiệu quả, sẵn sàng tự tin chinh phục điểm cao, vững bước vào đại học mơ ước nhờ phương pháp học trực quan, khoa học và hiệu quả học tập vượt trội!

Lý thuyết Biểu thức tọa độ của các phép toán vecto Toán 12 Chân trời sáng tạo

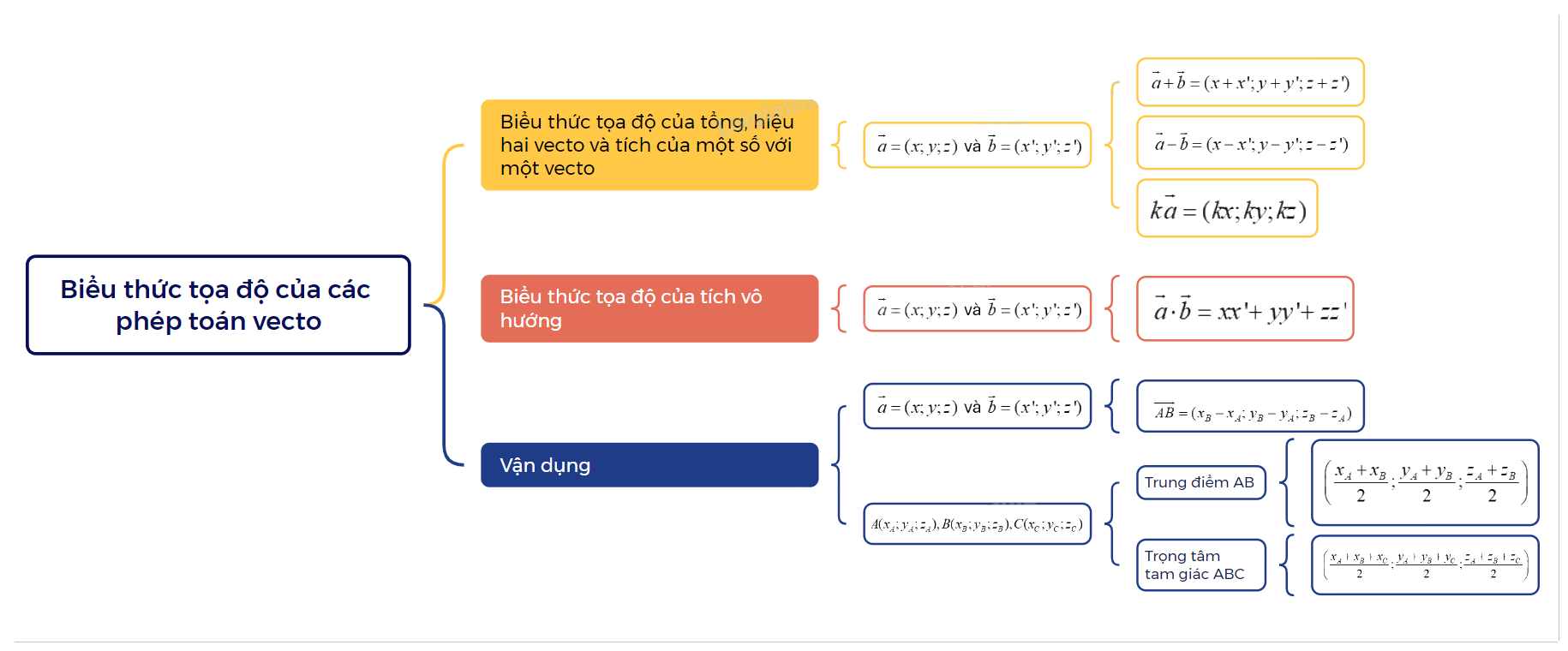
Trong chương trình Toán 12, phần Hình học Vectơ đóng vai trò quan trọng, đặc biệt là kiến thức về biểu thức tọa độ của các phép toán vecto. Việc nắm vững lý thuyết này không chỉ giúp học sinh giải quyết các bài toán trong sách giáo khoa mà còn là nền tảng cho các kiến thức nâng cao hơn trong chương trình đại học.

1. Khái niệm cơ bản về Vectơ

Vectơ là một đoạn thẳng có hướng. Trong không gian, một vectơ được xác định bởi điểm gốc và điểm cuối của nó. Vectơ có các đặc trưng quan trọng như độ dài (magnitude) và hướng (direction). Biểu diễn một vectơ thường sử dụng ký hiệu AB, trong đó A là điểm gốc và B là điểm cuối.

2. Tọa độ của Vectơ

Trong hệ tọa độ Descartes, một vectơ có thể được biểu diễn bằng tọa độ. Ví dụ, nếu A(x_A, y_A, z_A) và B(x_B, y_B, z_B) là hai điểm trong không gian, thì vectơ AB có tọa độ là (x_B - x_A, y_B - y_A, z_B - z_A).

3. Các phép toán trên Vectơ và Biểu thức Tọa độ

Phép cộng Vectơ: Cho hai vectơ a = (x₁, y₁, z₁) và b = (x₂, y₂, z₂), thì a + b = (x₁ + x₂, y₁ + y₂, z₁ + z₂).
Phép trừ Vectơ: Cho hai vectơ a = (x₁, y₁, z₁) và b = (x₂, y₂, z₂), thì a - b = (x₁ - x₂, y₁ - y₂, z₁ - z₂).
Phép nhân Vectơ với một số: Cho vectơ a = (x, y, z) và một số thực k, thì ka = (kx, ky, kz).
Tích vô hướng: Cho hai vectơ a = (x₁, y₁, z₁) và b = (x₂, y₂, z₂), thì a . b = x₁x₂ + y₁y₂ + z₁z₂.
Tích có hướng: Cho hai vectơ a = (x₁, y₁, z₁) và b = (x₂, y₂, z₂), thì a x b = (y₁z₂ - z₁y₂, z₁x₂ - x₁z₂, x₁y₂ - y₁x₂).

4. Ứng dụng của Biểu thức Tọa độ trong các bài toán Hình học

Biểu thức tọa độ của các phép toán vecto được ứng dụng rộng rãi trong việc giải các bài toán hình học không gian, như:

Chứng minh các đẳng thức vecto: Sử dụng các công thức cộng, trừ, nhân vectơ để biến đổi và chứng minh các đẳng thức.
Tìm tọa độ của các điểm: Sử dụng các phép toán vecto để xác định tọa độ của các điểm trong không gian.
Tính góc giữa hai vectơ: Sử dụng công thức tích vô hướng để tính góc giữa hai vectơ.
Tính diện tích hình bình hành và thể tích hình hộp: Sử dụng tích có hướng để tính diện tích hình bình hành và thể tích hình hộp.

5. Ví dụ minh họa

Ví dụ 1: Cho A(1, 2, 3) và B(4, 5, 6). Tìm tọa độ của vectơ AB.

Giải:AB = (4 - 1, 5 - 2, 6 - 3) = (3, 3, 3).

Ví dụ 2: Cho a = (1, 2, 3) và b = (4, 5, 6). Tính a . b.

Giải:a . b = 1*4 + 2*5 + 3*6 = 4 + 10 + 18 = 32.

6. Luyện tập và Củng cố

Để nắm vững kiến thức về biểu thức tọa độ của các phép toán vecto, bạn nên luyện tập thêm nhiều bài tập khác nhau. Hãy tìm các bài tập trong sách giáo khoa, sách bài tập hoặc trên các trang web học toán trực tuyến. Việc giải bài tập thường xuyên sẽ giúp bạn hiểu sâu hơn về lý thuyết và rèn luyện kỹ năng giải toán.

Hy vọng bài học này đã cung cấp cho bạn những kiến thức hữu ích về lý thuyết Biểu thức tọa độ của các phép toán vecto Toán 12 Chân trời sáng tạo. Chúc bạn học tốt!