Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 6, 7, 8 sách giáo khoa Toán 12 tập 1 chương trình Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Tính đơn điệu của hàm số
Trả lời câu hỏi Thực hành 3 trang 9 SGK Toán 12 Chân trời sáng tạo
Chứng minh rằng hàm số \(f\left( x \right) = 3x - sinx\) đồng biến trên \(\mathbb{R}\)
Phương pháp giải:
Tìm tập xác định D, đạo hàm f’(x) và dựa vào tính chất \( - 1 \le \cos x \le 1\)
Lời giải chi tiết:
Tập xác định: \(D = \mathbb{R}\)
\(f'(x) = 3 - \cos x\)
Ta có: \( - 1 \le \cos x \le 1\) nên \(2 \le 3 - \cos x \le 4\). Vì vậy \(f'(x) > 0\forall x \in \mathbb{R}\)
=> Hàm số \(f\left( x \right){\rm{ }} = {\rm{ }}3x{\rm{ }} - {\rm{ }}sinx\) đồng biến trên \(\mathbb{R}\)
Trả lời câu hỏi Khám phá 1 trang 7 SGK Toán 12 Chân trời sáng tạo
Cho hàm số y = f(x) = \({x^2}\)
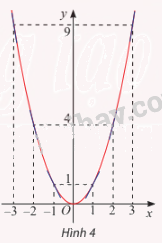
a) Từ đồ thị của hàm số y = f(x) (Hình 4), hãy chỉ ra các
khoảng đồng biến và nghịch biến của hàm số đã cho.
b) Tính đạo hàm f '(x) và xét dấu f '(x).
c) Từ đó, nhận xét về mối liên hệ giữa các khoảng đồng biến,
nghịch biến của hàm số với dấu của f '(x).
Phương pháp giải:
a) Hàm số y = f(x) gọi là đồng biến (tăng) trên K nếu với mọi \({x_1}\), \({x_2}\) thuộc K mà \({x_1}\) < \({x_2}\) thì f(\({x_1}\)) < f(\({x_2}\)). Hàm số y = f(x) gọi là nghịch biến (giảm) trên K nếu với mọi \({x_1}\), \({x_2}\) thuộc K mà \({x_1}\) < \({x_2}\) thì f(\({x_1}\)) > f(\({x_2}\)).
b) Dựa vào công thức đạo hàm để tìm f '(x)
c) So sánh và rút ra nhận xét
Lời giải chi tiết:
a) Hàm số đồng biến trên khoảng (0; \( + \infty \))
Hàm số nghịch biến trên khoảng (\( - \infty \); 0)
b) f '(x) = (\({x^2}\))' = 2x
Ta có:
f '(x) > 0 \( \Leftrightarrow 2x > 0 \Leftrightarrow x > 0\)
f '(x) < 0 \( \Leftrightarrow 2x < 0 \Leftrightarrow x < 0\)
c) Nhận xét:
f’(x) > 0 trên K thì y = f(x) đồng biến trên K
f’(x) < 0 trên K thì y = f(x) nghịch biến trên K
Trả lời câu hỏi Thực hành 2 trang 9 SGK Toán 12 Chân trời sáng tạo
Xét tính đơn điệu của các hàm số sau:
a) \(f(x) = {x^3} - 6{x^2} + 9x\)
b) \(g(x) = \frac{1}{x}\)
Phương pháp giải:
Xác định tập xác định D, đạo hàm f’(x) và lập bảng biến thiên
Lời giải chi tiết:
a) \(f(x) = {x^3} - 6{x^2} + 9x\)
Tập xác định: \(D = \mathbb{R}\)
\(f'(x) = 3{x^2} - 12x + 9\)
\(f'(x) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = 1\end{array} \right.\)
Bảng biến thiên:
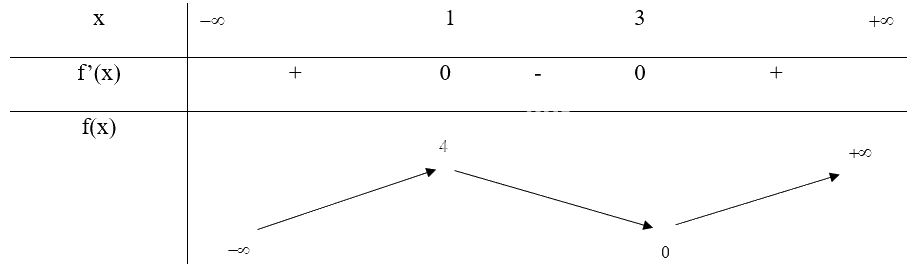
Vậy hàm số \(f(x) = {x^3} - 6{x^2} + 9x\) đồng biến trên các khoảng (\( - \infty \); 1) và (3; \( + \infty \)), nghịch biến trên khoảng (1; 3)
b) \(g(x) = \frac{1}{x}\)
Tập xác định: \(D = \mathbb{R}\backslash \{ 0\} \)
\(g'(x) = - \frac{1}{{{x^2}}}\)
Vì \({x^2} > 0\forall x \in \mathbb{R}\backslash \{ 0\} \) nên \(g'(x) < 0\forall x \in \mathbb{R}\backslash \{ 0\} \)
Bảng biến thiên:
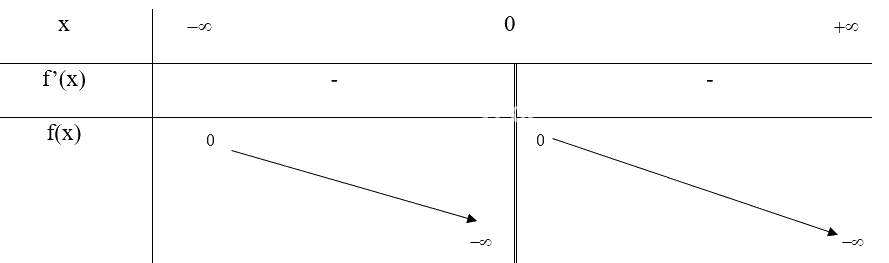
Vậy hàm số \(g(x) = \frac{1}{x}\) nghịch biến trên các khoảng (\( - \infty \); 0) và (0; \( + \infty \))
Trả lời câu hỏi Thực hành 1 trang 7 SGK Toán 12 Chân trời sáng tạo
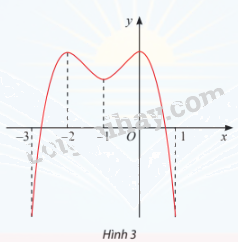
Tìm các khoảng đơn điệu của hàm số y = f(x) có đồ thị cho ở Hình 3.
Phương pháp giải:
Hàm số y = f(x) gọi là đồng biến (tăng) trên K nếu với mọi \({x_1}\), \({x_2}\) thuộc K mà \({x_1}\) < \({x_2}\) thì f(\({x_1}\)) < f(\({x_2}\)). Hàm số y = f(x) gọi là nghịch biến (giảm) trên K nếu với mọi \({x_1}\), \({x_2}\) thuộc K mà \({x_1}\) < \({x_2}\) thì f(\({x_1}\)) > f(\({x_2}\)).
Lời giải chi tiết:
Hàm số đồng biến trên các khoảng (−3; -2) và (-1; 0)
Hàm số nghịch biến trên khoảng (-2; -1) và (0; 1)
Trả lời câu hỏi Vận dụng 1 trang 9 SGK Toán 12 Chân trời sáng tạo
Hãy trả lời câu hỏi trong Khởi động (trang 6) bằng cách xét dấu đạo hàm của hàm số \(h\left( t \right) = 6{t^3} - 81{t^2} + 324t\) với \(0 \le t \le 8\)
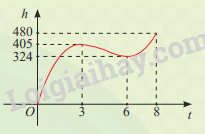
Trong 8 phút đầu kể từ khi xuất phát, độ cao h (tính bằng mét) của khinh khí cầu vào thời điểm t phút được cho bởi công thức \(h\left( t \right) = 6{t^3} - 81{t^2} + 324t\). Đồ thị của hàm số h(t) được biểu diễn trong hình bên. Trong các khoảng thời gian nào khinh khí cầu tăng dần độ cao, giảm dần độ cao? Độ cao của khinh khí cầu vào các thời điểm 3 phút và 6 phút sau khi xuất phát có gì đặc biệt?
Phương pháp giải:
Xét dấu h’(x) để tìm ra các khoảng đồng biến, nghịch biến
Lời giải chi tiết:
\(h\left( t \right) = 6{t^3} - 81{t^2} + 324t\)
Tập xác định: \(D = \mathbb{R}\)
\(h'(t) = 18{t^2} - 162t + 324\)
\(h'(t) = 0 \Leftrightarrow \left[ \begin{array}{l}t = 3\\t = 6\end{array} \right.\)
Bảng biến thiên:
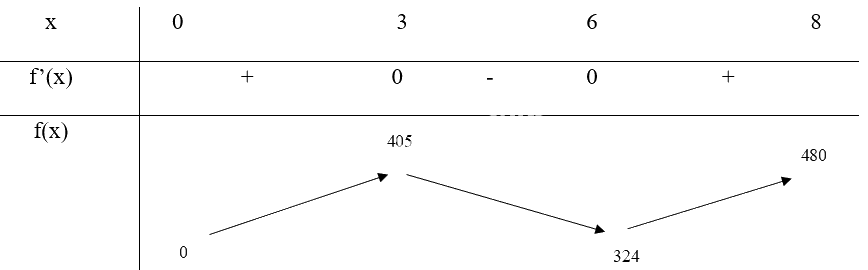
Trong thời gian từ lúc xuất phát đến thời điểm 3 phút, độ cao của khinh khí cầu tăng dần từ 0m lên 405m
Độ cao của khinh khí cầu tăng dần từ 0m lên 405m trong thời gian từ lúc xuất phát đến thời điểm 3 phút, từ 324m lên 480m trong thời gian từ 6 phút đến 8 phút
Độ cao của khinh khí cầu giảm dần từ 405m xuống 324m trong thời gian từ 3 phút đến 6 phút
Trả lời câu hỏi Thực hành 1 trang 7 SGK Toán 12 Chân trời sáng tạo
Tìm các khoảng đơn điệu của hàm số y = f(x) có đồ thị cho ở Hình 3.
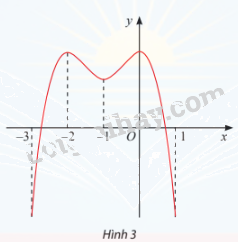
Phương pháp giải:
Hàm số y = f(x) gọi là đồng biến (tăng) trên K nếu với mọi \({x_1}\), \({x_2}\) thuộc K mà \({x_1}\) < \({x_2}\) thì f(\({x_1}\)) < f(\({x_2}\)). Hàm số y = f(x) gọi là nghịch biến (giảm) trên K nếu với mọi \({x_1}\), \({x_2}\) thuộc K mà \({x_1}\) < \({x_2}\) thì f(\({x_1}\)) > f(\({x_2}\)).
Lời giải chi tiết:
Hàm số đồng biến trên các khoảng (−3; -2) và (-1; 0)
Hàm số nghịch biến trên khoảng (-2; -1) và (0; 1)
Trả lời câu hỏi Khám phá 1 trang 7 SGK Toán 12 Chân trời sáng tạo
Cho hàm số y = f(x) = \({x^2}\)
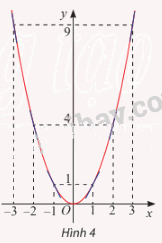
a) Từ đồ thị của hàm số y = f(x) (Hình 4), hãy chỉ ra các
khoảng đồng biến và nghịch biến của hàm số đã cho.
b) Tính đạo hàm f '(x) và xét dấu f '(x).
c) Từ đó, nhận xét về mối liên hệ giữa các khoảng đồng biến,
nghịch biến của hàm số với dấu của f '(x).
Phương pháp giải:
a) Hàm số y = f(x) gọi là đồng biến (tăng) trên K nếu với mọi \({x_1}\), \({x_2}\) thuộc K mà \({x_1}\) < \({x_2}\) thì f(\({x_1}\)) < f(\({x_2}\)). Hàm số y = f(x) gọi là nghịch biến (giảm) trên K nếu với mọi \({x_1}\), \({x_2}\) thuộc K mà \({x_1}\) < \({x_2}\) thì f(\({x_1}\)) > f(\({x_2}\)).
b) Dựa vào công thức đạo hàm để tìm f '(x)
c) So sánh và rút ra nhận xét
Lời giải chi tiết:
a) Hàm số đồng biến trên khoảng (0; \( + \infty \))
Hàm số nghịch biến trên khoảng (\( - \infty \); 0)
b) f '(x) = (\({x^2}\))' = 2x
Ta có:
f '(x) > 0 \( \Leftrightarrow 2x > 0 \Leftrightarrow x > 0\)
f '(x) < 0 \( \Leftrightarrow 2x < 0 \Leftrightarrow x < 0\)
c) Nhận xét:
f’(x) > 0 trên K thì y = f(x) đồng biến trên K
f’(x) < 0 trên K thì y = f(x) nghịch biến trên K
Trả lời câu hỏi Thực hành 2 trang 9 SGK Toán 12 Chân trời sáng tạo
Xét tính đơn điệu của các hàm số sau:
a) \(f(x) = {x^3} - 6{x^2} + 9x\)
b) \(g(x) = \frac{1}{x}\)
Phương pháp giải:
Xác định tập xác định D, đạo hàm f’(x) và lập bảng biến thiên
Lời giải chi tiết:
a) \(f(x) = {x^3} - 6{x^2} + 9x\)
Tập xác định: \(D = \mathbb{R}\)
\(f'(x) = 3{x^2} - 12x + 9\)
\(f'(x) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = 1\end{array} \right.\)
Bảng biến thiên:
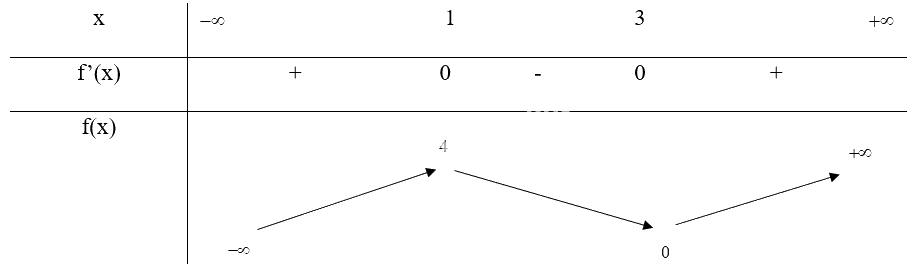
Vậy hàm số \(f(x) = {x^3} - 6{x^2} + 9x\) đồng biến trên các khoảng (\( - \infty \); 1) và (3; \( + \infty \)), nghịch biến trên khoảng (1; 3)
b) \(g(x) = \frac{1}{x}\)
Tập xác định: \(D = \mathbb{R}\backslash \{ 0\} \)
\(g'(x) = - \frac{1}{{{x^2}}}\)
Vì \({x^2} > 0\forall x \in \mathbb{R}\backslash \{ 0\} \) nên \(g'(x) < 0\forall x \in \mathbb{R}\backslash \{ 0\} \)
Bảng biến thiên:
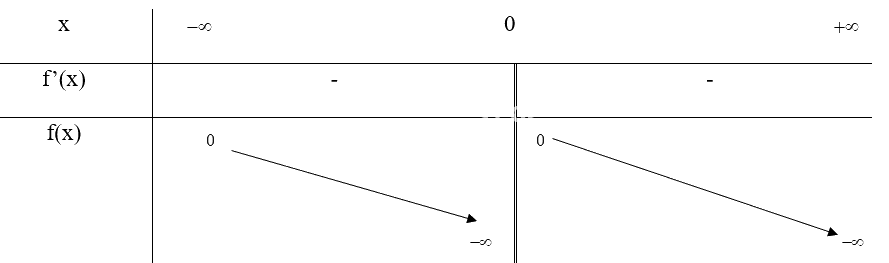
Vậy hàm số \(g(x) = \frac{1}{x}\) nghịch biến trên các khoảng (\( - \infty \); 0) và (0; \( + \infty \))
Trả lời câu hỏi Thực hành 3 trang 9 SGK Toán 12 Chân trời sáng tạo
Chứng minh rằng hàm số \(f\left( x \right) = 3x - sinx\) đồng biến trên \(\mathbb{R}\)
Phương pháp giải:
Tìm tập xác định D, đạo hàm f’(x) và dựa vào tính chất \( - 1 \le \cos x \le 1\)
Lời giải chi tiết:
Tập xác định: \(D = \mathbb{R}\)
\(f'(x) = 3 - \cos x\)
Ta có: \( - 1 \le \cos x \le 1\) nên \(2 \le 3 - \cos x \le 4\). Vì vậy \(f'(x) > 0\forall x \in \mathbb{R}\)
=> Hàm số \(f\left( x \right){\rm{ }} = {\rm{ }}3x{\rm{ }} - {\rm{ }}sinx\) đồng biến trên \(\mathbb{R}\)
Trả lời câu hỏi Vận dụng 1 trang 9 SGK Toán 12 Chân trời sáng tạo
Hãy trả lời câu hỏi trong Khởi động (trang 6) bằng cách xét dấu đạo hàm của hàm số \(h\left( t \right) = 6{t^3} - 81{t^2} + 324t\) với \(0 \le t \le 8\)
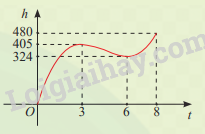
Trong 8 phút đầu kể từ khi xuất phát, độ cao h (tính bằng mét) của khinh khí cầu vào thời điểm t phút được cho bởi công thức \(h\left( t \right) = 6{t^3} - 81{t^2} + 324t\). Đồ thị của hàm số h(t) được biểu diễn trong hình bên. Trong các khoảng thời gian nào khinh khí cầu tăng dần độ cao, giảm dần độ cao? Độ cao của khinh khí cầu vào các thời điểm 3 phút và 6 phút sau khi xuất phát có gì đặc biệt?
Phương pháp giải:
Xét dấu h’(x) để tìm ra các khoảng đồng biến, nghịch biến
Lời giải chi tiết:
\(h\left( t \right) = 6{t^3} - 81{t^2} + 324t\)
Tập xác định: \(D = \mathbb{R}\)
\(h'(t) = 18{t^2} - 162t + 324\)
\(h'(t) = 0 \Leftrightarrow \left[ \begin{array}{l}t = 3\\t = 6\end{array} \right.\)
Bảng biến thiên:
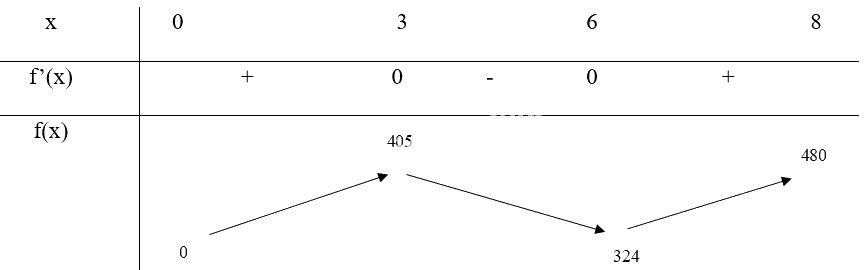
Trong thời gian từ lúc xuất phát đến thời điểm 3 phút, độ cao của khinh khí cầu tăng dần từ 0m lên 405m
Độ cao của khinh khí cầu tăng dần từ 0m lên 405m trong thời gian từ lúc xuất phát đến thời điểm 3 phút, từ 324m lên 480m trong thời gian từ 6 phút đến 8 phút
Độ cao của khinh khí cầu giảm dần từ 405m xuống 324m trong thời gian từ 3 phút đến 6 phút
Mục 1 của chương trình Toán 12 tập 1 Chân trời sáng tạo tập trung vào việc ôn tập và mở rộng kiến thức về hàm số và đồ thị. Các bài tập trong mục này thường yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, đồng thời rèn luyện kỹ năng tư duy logic và phân tích.
Bài 1 tập trung vào việc nhắc lại định nghĩa hàm số, tập xác định, tập giá trị và các khái niệm liên quan đến tính liên tục của hàm số. Các bài tập thường yêu cầu học sinh xác định tập xác định, tập giá trị của hàm số, xét tính liên tục của hàm số tại một điểm hoặc trên một khoảng.
Bài 2 giới thiệu về khái niệm giới hạn của hàm số tại một điểm và tại vô cùng. Các bài tập thường yêu cầu học sinh tính giới hạn của hàm số, chứng minh sự tồn tại của giới hạn và ứng dụng giới hạn để giải quyết các bài toán thực tế.
Bài 3 giới thiệu về khái niệm đạo hàm của hàm số tại một điểm và đạo hàm của hàm số trên một khoảng. Các bài tập thường yêu cầu học sinh tính đạo hàm của hàm số, tìm đạo hàm cấp hai và ứng dụng đạo hàm để giải quyết các bài toán liên quan đến tiếp tuyến, cực trị và sự biến thiên của hàm số.
| Hàm số | Đạo hàm |
|---|---|
| y = x² | y' = 2x |
| y = sin(x) | y' = cos(x) |
Để giải các bài tập trong mục 1 một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về hàm số, giới hạn và đạo hàm. Bên cạnh đó, cần rèn luyện kỹ năng biến đổi đại số, sử dụng các công thức đạo hàm và áp dụng các phương pháp giải toán phù hợp.
Một số phương pháp giải bài tập thường được sử dụng:
Để học tốt môn Toán 12, học sinh cần:
Giaitoan.edu.vn hy vọng rằng với lời giải chi tiết và những hướng dẫn hữu ích này, các em sẽ tự tin hơn trong việc học tập và giải quyết các bài tập Toán 12 tập 1 Chân trời sáng tạo.