Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 1 trang 52,53 SGK Toán 12 tập 1 chương trình Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập một cách khoa học.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, tự tin giải quyết các bài toán Toán 12 và đạt kết quả cao trong học tập.
Hệ toạ độ trong không gian
Trả lời câu hỏi Thực hành 1 trang 53 SGK Toán 12 Chân trời sáng tạo
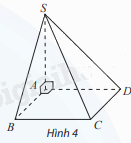
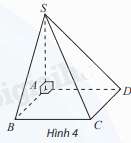
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 1, SA vuông góc với mặt phẳng đáy và có độ dài bằng 1 (Hình 4). Vẽ hệ trục toạ độ Oxyz có gốc O trùng với điểm A, các điểm B, D, S lần lượt nằm trên các tia Ox, Oy, Oz và chỉ ra các vectơ đơn vị trên các trục toạ độ.
Phương pháp giải:
Vẽ một hệ trục tọa độ Oxyz và quan sát hình vẽ.
Lời giải chi tiết:
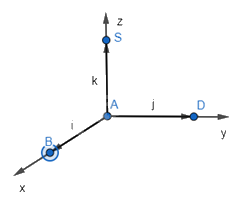
Các vecto đơn vị của Ox, Oy, Oz lần lượt là \(\overrightarrow i = \overrightarrow {AB} \), \(\overrightarrow j = \overrightarrow {AD} \), \(\overrightarrow k = \overrightarrow {AS} \).
Trả lời câu hỏi Khám phá 1 trang 52 SGK Toán 12 Chân trời sáng tạo
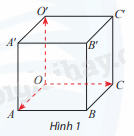
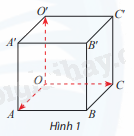
Cho hình lập phương OABC.O′A′B′C′ có cạnh bằng 1. Đặt \(\overrightarrow i = \overrightarrow {OA} ;\overrightarrow j = \overrightarrow {OC} ;\overrightarrow k = \overrightarrow {OO'} \)
a) Nêu nhận xét về phương và độ dài của ba vectơ \(\overrightarrow i \), \(\overrightarrow j \), \(\overrightarrow k \).
b) Nêu nhận xét về ba trục toạ độ \((O,\overrightarrow i )\) , \((O,\overrightarrow j )\) , \((O,\overrightarrow k )\).
Phương pháp giải:
Quan sát hình vẽ.
Lời giải chi tiết:
a) Độ dài 3 vecto \(\overrightarrow i \), \(\overrightarrow j \), \(\overrightarrow k \) bằng nhau: |\(\overrightarrow i \)| = |\(\overrightarrow j \)| = |\(\overrightarrow k \)|.
b) Ba trục toạ độ \((O,\overrightarrow i )\) , \((O,\overrightarrow j )\) , \((O,\overrightarrow k )\) đôi một vuông góc với nhau.
Trả lời câu hỏi Vận dụng 1 trang 53 SGK Toán 12 Chân trời sáng tạo
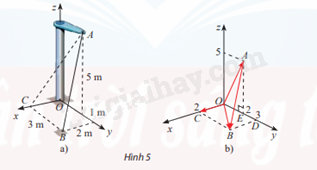
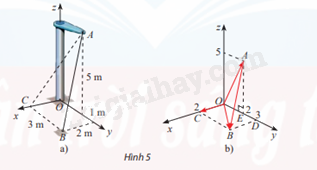
Một thiết kế cơ khí trong Hình 5a được biểu diễn trong không gian Oxyz như Hình 5b.
a) Hãy vẽ ba vectơ đơn vị \(\overrightarrow i \), \(\overrightarrow j \), \(\overrightarrow k \) lần lượt trên ba trục toạ độ Ox, Oy, Oz (mỗi vectơ đơn vị có độ dài bằng 1m).
b) Biểu diễn các vectơ \(\overrightarrow {OC} ,\overrightarrow {OB} ,\overrightarrow {OA} ,\overrightarrow {AB} \) theo \(\overrightarrow i \), \(\overrightarrow j \), \(\overrightarrow k \).
Phương pháp giải:
Quan sát hình vẽ.
Lời giải chi tiết:
a)
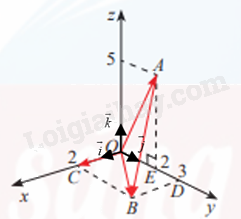
b) \(\overrightarrow {OC} = 2\overrightarrow i \).
\(\overrightarrow {OB} = 2\overrightarrow i + 3\overrightarrow j \).
\(\overrightarrow {OA} = 2\overrightarrow j + 5\overrightarrow k \).
\(\overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {OA} = \left( {2\overrightarrow i + 3\overrightarrow j } \right) - \left( {2\overrightarrow j + 5\overrightarrow k } \right) = 2\overrightarrow i + \overrightarrow j - 5\overrightarrow k \).
Trả lời câu hỏi Khám phá 1 trang 52 SGK Toán 12 Chân trời sáng tạo
Cho hình lập phương OABC.O′A′B′C′ có cạnh bằng 1. Đặt \(\overrightarrow i = \overrightarrow {OA} ;\overrightarrow j = \overrightarrow {OC} ;\overrightarrow k = \overrightarrow {OO'} \)
a) Nêu nhận xét về phương và độ dài của ba vectơ \(\overrightarrow i \), \(\overrightarrow j \), \(\overrightarrow k \).
b) Nêu nhận xét về ba trục toạ độ \((O,\overrightarrow i )\) , \((O,\overrightarrow j )\) , \((O,\overrightarrow k )\).
Phương pháp giải:
Quan sát hình vẽ.
Lời giải chi tiết:
a) Độ dài 3 vecto \(\overrightarrow i \), \(\overrightarrow j \), \(\overrightarrow k \) bằng nhau: |\(\overrightarrow i \)| = |\(\overrightarrow j \)| = |\(\overrightarrow k \)|.
b) Ba trục toạ độ \((O,\overrightarrow i )\) , \((O,\overrightarrow j )\) , \((O,\overrightarrow k )\) đôi một vuông góc với nhau.
Trả lời câu hỏi Thực hành 1 trang 53 SGK Toán 12 Chân trời sáng tạo
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 1, SA vuông góc với mặt phẳng đáy và có độ dài bằng 1 (Hình 4). Vẽ hệ trục toạ độ Oxyz có gốc O trùng với điểm A, các điểm B, D, S lần lượt nằm trên các tia Ox, Oy, Oz và chỉ ra các vectơ đơn vị trên các trục toạ độ.
Phương pháp giải:
Vẽ một hệ trục tọa độ Oxyz và quan sát hình vẽ.
Lời giải chi tiết:
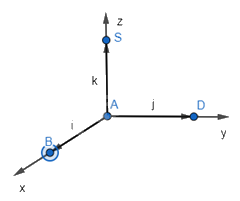
Các vecto đơn vị của Ox, Oy, Oz lần lượt là \(\overrightarrow i = \overrightarrow {AB} \), \(\overrightarrow j = \overrightarrow {AD} \), \(\overrightarrow k = \overrightarrow {AS} \).
Trả lời câu hỏi Vận dụng 1 trang 53 SGK Toán 12 Chân trời sáng tạo
Một thiết kế cơ khí trong Hình 5a được biểu diễn trong không gian Oxyz như Hình 5b.
a) Hãy vẽ ba vectơ đơn vị \(\overrightarrow i \), \(\overrightarrow j \), \(\overrightarrow k \) lần lượt trên ba trục toạ độ Ox, Oy, Oz (mỗi vectơ đơn vị có độ dài bằng 1m).
b) Biểu diễn các vectơ \(\overrightarrow {OC} ,\overrightarrow {OB} ,\overrightarrow {OA} ,\overrightarrow {AB} \) theo \(\overrightarrow i \), \(\overrightarrow j \), \(\overrightarrow k \).
Phương pháp giải:
Quan sát hình vẽ.
Lời giải chi tiết:
a)
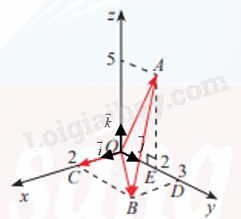
b) \(\overrightarrow {OC} = 2\overrightarrow i \).
\(\overrightarrow {OB} = 2\overrightarrow i + 3\overrightarrow j \).
\(\overrightarrow {OA} = 2\overrightarrow j + 5\overrightarrow k \).
\(\overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {OA} = \left( {2\overrightarrow i + 3\overrightarrow j } \right) - \left( {2\overrightarrow j + 5\overrightarrow k } \right) = 2\overrightarrow i + \overrightarrow j - 5\overrightarrow k \).
Mục 1 của chương trình Toán 12 tập 1 Chân trời sáng tạo thường tập trung vào các khái niệm cơ bản về giới hạn của hàm số. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương tiếp theo. Bài tập trang 52, 53 SGK là cơ hội để học sinh rèn luyện và củng cố kiến thức đã học.
Các bài tập trong mục này thường yêu cầu học sinh:
Để giải các bài tập về giới hạn, học sinh cần nắm vững các phương pháp sau:
Bài 1: Tính limx→2 (x2 - 4) / (x - 2)
Giải:
Ta có: (x2 - 4) / (x - 2) = (x - 2)(x + 2) / (x - 2) = x + 2 (với x ≠ 2)
Vậy, limx→2 (x2 - 4) / (x - 2) = limx→2 (x + 2) = 2 + 2 = 4
Ngoài SGK Toán 12 tập 1 Chân trời sáng tạo, học sinh có thể tham khảo thêm các tài liệu sau:
Việc giải bài tập mục 1 trang 52,53 SGK Toán 12 tập 1 Chân trời sáng tạo đòi hỏi học sinh phải nắm vững kiến thức về giới hạn và các phương pháp giải bài tập liên quan. Hy vọng với những hướng dẫn chi tiết và ví dụ minh họa trên, các em sẽ tự tin hơn trong quá trình học tập và đạt kết quả tốt nhất.