Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập Toán 12 tập 2. Bài viết này sẽ hướng dẫn bạn giải bài tập 4 trang 75 SGK Toán 12 tập 2 theo chương trình Chân trời sáng tạo.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi luôn cố gắng trình bày lời giải một cách dễ hiểu nhất, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Máy tính và thiết bị lưu điện (UPS) được kết nối như hình dưới đây. Khi xảy ra sự cố điện, UPS bị hỏng với xác suất 0,02. Nếu UPS bị hỏng khi xảy ra sự cố điện, máy tính sẽ bị hỏng với xác suất 0,1; ngược lại, nếu UPS không bị hỏng, máy tính sẽ không bị hỏng. a) Tính xác suất để cả UPS và máy tính đều không bị hỏng khi xảy ra sự cố điện. b) Tính xác suất để cả UPS và máy tính đều bị hỏng khi xảy ra sự cố điện.
Đề bài
Máy tính và thiết bị lưu điện (UPS) được kết nối như hình dưới đây. Khi xảy ra sự cố điện, UPS bị hỏng với xác suất 0,02. Nếu UPS bị hỏng khi xảy ra sự cố điện, máy tính sẽ bị hỏng với xác suất 0,1; ngược lại, nếu UPS không bị hỏng, máy tính sẽ không bị hỏng.
a) Tính xác suất để cả UPS và máy tính đều không bị hỏng khi xảy ra sự cố điện.
b) Tính xác suất để cả UPS và máy tính đều bị hỏng khi xảy ra sự cố điện.

Phương pháp giải - Xem chi tiết
Gọi \(M\) là biến cố “UPS không bị hỏng”, \(N\) là biến cố “Máy tính không bị hỏng”.
Sử dụng sơ đồ hình cây, từ đó tính được xác suất của các biến cố mà đề bài yêu cầu.
Lời giải chi tiết
Gọi \(M\) là biến cố “UPS không bị hỏng”, \(N\) là biến cố “Máy tính không bị hỏng”.
Theo đề bài, ta có sơ đồ hình cây sau:
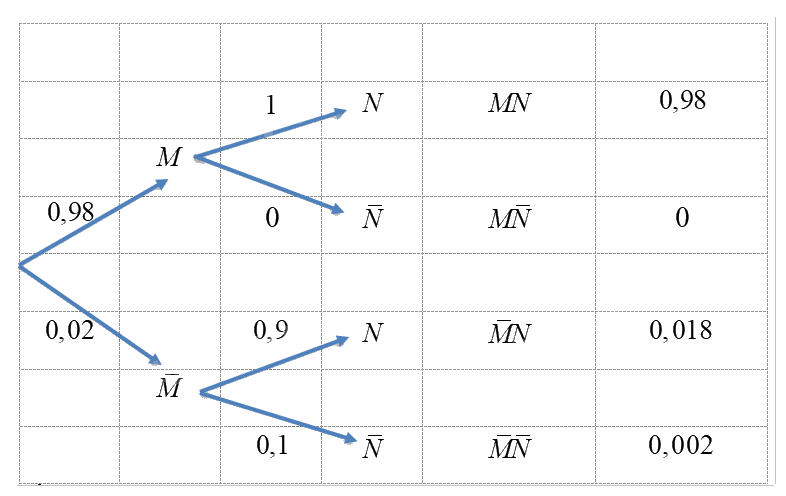
Từ sơ đồ hình cây, ta suy ra:
a) Xác suất để cả UPS và máy tính không bị hỏng là \(P\left( {MN} \right) = 0,98.\)
b) Xác suất để cả UPS và máy tính bị hỏng là \(P\left( {\bar M\bar N} \right) = 0,002.\)
Bài tập 4 trang 75 SGK Toán 12 tập 2 thuộc chương trình Chân trời sáng tạo, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế liên quan đến tốc độ thay đổi của đại lượng. Bài tập này thường yêu cầu học sinh phải hiểu rõ các khái niệm như đạo hàm, quy tắc tính đạo hàm, và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.
Bài tập 4 thường bao gồm các dạng bài sau:
Để giúp bạn hiểu rõ hơn về cách giải bài tập này, chúng tôi sẽ trình bày lời giải chi tiết cho từng phần của bài tập.
Để xác định vận tốc tức thời của một vật chuyển động, ta cần tìm đạo hàm của hàm vị trí theo thời gian. Vận tốc tức thời tại thời điểm t được tính bằng công thức:
v(t) = s'(t)
Trong đó:
Để tìm đạo hàm của hàm số hợp, ta sử dụng quy tắc chuỗi. Quy tắc chuỗi phát biểu rằng:
(f(g(x)))' = f'(g(x)) * g'(x)
Trong đó:
Để giải bài toán tối ưu hóa, ta cần tìm giá trị lớn nhất hoặc nhỏ nhất của một hàm số trên một khoảng cho trước. Để tìm cực trị của hàm số, ta thực hiện các bước sau:
Giả sử một vật chuyển động theo hàm vị trí s(t) = t^3 - 3t^2 + 2t. Hãy tìm vận tốc tức thời của vật tại thời điểm t = 2.
Lời giải:
Ta có s'(t) = 3t^2 - 6t + 2. Thay t = 2 vào, ta được v(2) = 3(2)^2 - 6(2) + 2 = 2.
Vậy vận tốc tức thời của vật tại thời điểm t = 2 là 2.
Ngoài SGK Toán 12 tập 2, bạn có thể tham khảo thêm các tài liệu sau:
Bài tập 4 trang 75 SGK Toán 12 tập 2 - Chân trời sáng tạo là một bài tập quan trọng giúp bạn củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc giải quyết các bài toán thực tế. Hy vọng rằng với lời giải chi tiết và các mẹo giải bài tập mà chúng tôi đã cung cấp, bạn sẽ tự tin hơn trong quá trình học tập.