Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12 tập 1 - Chân trời sáng tạo. Bài viết này sẽ hướng dẫn bạn giải bài tập 4 trang 18 một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập môn Toán.
Khi làm nhà kho, bác An muốn cửa sổ có dạng hình chữ nhật với chu vi bằng 4m (Hình 6). Tìm kích thước khung cửa sổ sao cho diện tích cửa sổ lớn nhất (để hứng được nhiều ánh sáng nhất)?
Đề bài
Khi làm nhà kho, bác An muốn cửa sổ có dạng hình chữ nhật với chu vi bằng 4m (Hình 6). Tìm kích thước khung cửa sổ sao cho diện tích cửa sổ lớn nhất (để hứng được nhiều ánh sáng nhất)?

Phương pháp giải - Xem chi tiết
Tìm mối liên hệ giữa chiều dài và chiều rộng của cửa, sau đó lập hàm số của diện tích cửa sổ, tìm đạo hàm, vẽ bảng biến thiên và xác định giá trị lớn nhất của diện tích.
Lời giải chi tiết
Gọi a, b lần lượt là chiều dài và chiều rộng của cửa sổ (m; a,b > 0).
Chu vi cửa sổ là: \(2(a + b) = 4 \Leftrightarrow b = 2 - a\).
Diện tích cửa sổ là: \(y = ab = a(2 - a) = - {a^2} + 2a\).
\(y' = - 2a + 2 = 0 \Leftrightarrow a = 1\).
Bảng biến thiên:
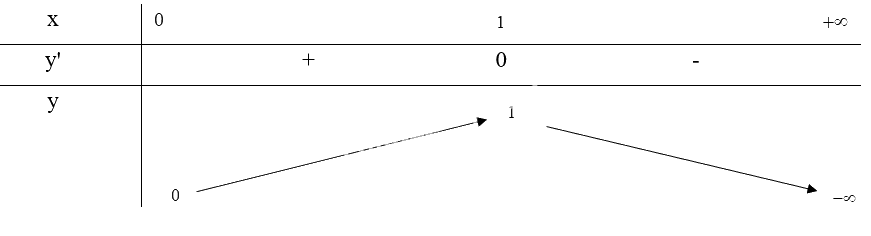
Từ bảng biến thiên, ta thấy \(\mathop {\max }\limits_{(0; + \infty )} y = y(1) = 1\).
Vậy để diện tích cửa sổ lớn nhất bằng 1 \{m^2}\) thì chiều dài và chiều rộng bằng nhau và bằng 1m.
Bài tập 4 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo thuộc chương trình học về giới hạn của hàm số. Bài tập này yêu cầu học sinh vận dụng kiến thức về giới hạn một bên, giới hạn tại một điểm và các tính chất của giới hạn để giải quyết các bài toán cụ thể. Việc nắm vững kiến thức nền tảng và kỹ năng giải bài tập là rất quan trọng để đạt kết quả tốt trong môn Toán.
Bài tập 4 bao gồm một số câu hỏi nhỏ, yêu cầu học sinh tính giới hạn của hàm số tại một điểm cho trước. Các hàm số có thể là hàm đa thức, hàm hữu tỉ hoặc hàm lượng giác. Để giải bài tập này, học sinh cần:
Dưới đây là lời giải chi tiết cho từng câu hỏi trong bài tập 4 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo:
Để tính giới hạn này, ta có thể thay trực tiếp x = 2 vào biểu thức:
limx→2 (x2 - 3x + 2) = 22 - 3*2 + 2 = 4 - 6 + 2 = 0
Tương tự như câu a, ta thay x = -1 vào biểu thức:
limx→-1 (x3 + 1) = (-1)3 + 1 = -1 + 1 = 0
Thay x = 0 vào biểu thức:
limx→0 (x2 + 2x + 1) = 02 + 2*0 + 1 = 0 + 0 + 1 = 1
Ngoài bài tập 4, còn rất nhiều bài tập tương tự về giới hạn hàm số. Để giải quyết các bài tập này, bạn có thể áp dụng các phương pháp sau:
Khi giải bài tập về giới hạn, bạn cần lưu ý những điều sau:
Để củng cố kiến thức và kỹ năng giải bài tập về giới hạn, bạn có thể tự giải các bài tập sau:
Bài tập 4 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo là một bài tập cơ bản về giới hạn hàm số. Việc nắm vững kiến thức và kỹ năng giải bài tập này sẽ giúp bạn tự tin hơn trong quá trình học tập môn Toán. Hãy luyện tập thường xuyên để củng cố kiến thức và đạt kết quả tốt nhất.