Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12 tập 1 - Chân trời sáng tạo. Bài viết này sẽ giúp bạn Giải bài tập 8 trang 51 một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và đạt kết quả cao trong môn Toán.
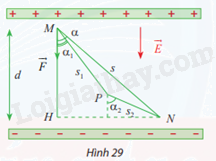
Một lực tĩnh điện \(\overrightarrow F \) tác động lên điện tích điểm M trong điện trường đều làm cho M dịch chuyển theo đường gấp khúc MNP (Hình 29). Biết \(q = {2.10^{ - 12}}C\), vectơ điện trường có độ lớn \(E = 1,{8.10^5}\)N/C và d = MH = 5mm. Tính công A sinh bởi lực tĩnh điện \(\overrightarrow F \).
Đề bài
Một lực tĩnh điện \(\overrightarrow F \) tác động lên điện tích điểm M trong điện trường đều làm cho M dịch chuyển theo đường gấp khúc MNP (Hình 29). Biết \(q = {2.10^{ - 12}}C\), vectơ điện trường có độ lớn \(E = 1,{8.10^5}\)N/C và d = MH = 5mm. Tính công A sinh bởi lực tĩnh điện \(\overrightarrow F \).
Phương pháp giải - Xem chi tiết
Áp dụng công thức tính công \(A = Fs\cos \alpha \)
Lời giải chi tiết
Đổi: 5mm = 0,005m
Gọi K là điểm thuộc MH sao cho \(PK \bot MH\), L là điểm thuộc HN sao cho \(PL \bot HN\)
\({A_{MNP}} = {A_{MP}} + {A_{PN}} = {F_d}.MP\cos {\alpha _1} + {F_d}.PN\cos {\alpha _2}\)
\( \Leftrightarrow {A_{MNP}} = qE.\frac{{MK}}{{\cos {\alpha _1}}}.\cos {\alpha _1} + qE.\frac{{PL}}{{\cos {\alpha _2}}}.\cos {\alpha _2}\)
\( \Leftrightarrow {A_{MNP}} = qE(MK + PL) = qE(MK + KH) = qE.MH = {2.10^{ - 12}}.1,{8.10^5}.0,005 = 1,{8.10^{ - 9}}J\)
Bài tập 8 trang 51 SGK Toán 12 tập 1 - Chân trời sáng tạo thuộc chương trình học về giới hạn của hàm số. Bài tập này yêu cầu học sinh vận dụng kiến thức về giới hạn một bên, giới hạn tại một điểm và các tính chất của giới hạn để giải quyết các bài toán cụ thể. Việc nắm vững kiến thức nền tảng và kỹ năng giải bài tập là rất quan trọng để học tốt môn Toán 12.
Bài tập 8 bao gồm các câu hỏi liên quan đến việc tính giới hạn của hàm số tại một điểm, sử dụng định nghĩa và các tính chất của giới hạn. Các hàm số thường gặp trong bài tập này là hàm đa thức, hàm hữu tỉ và hàm lượng giác. Để giải quyết bài tập này, học sinh cần:
Dưới đây là lời giải chi tiết cho từng câu hỏi trong bài tập 8 trang 51 SGK Toán 12 tập 1 - Chân trời sáng tạo:
Để giải câu a, ta cần tính giới hạn của hàm số f(x) khi x tiến tới một giá trị cụ thể. Ta có thể sử dụng định nghĩa giới hạn hoặc các tính chất của giới hạn để tìm ra kết quả.
Ví dụ:
lim (x->2) (x^2 - 4) / (x - 2) = lim (x->2) (x + 2) = 4Tương tự như câu a, ta cần áp dụng các kiến thức và kỹ năng đã học để tính giới hạn của hàm số f(x) khi x tiến tới một giá trị khác.
Ví dụ:
lim (x->0) sin(x) / x = 1Câu c có thể yêu cầu học sinh chứng minh một giới hạn nào đó hoặc tìm điều kiện để giới hạn tồn tại. Trong trường hợp này, ta cần sử dụng các định lý và tính chất của giới hạn một cách linh hoạt.
Ngoài bài tập 8, còn rất nhiều bài tập tương tự về giới hạn hàm số trong SGK Toán 12 tập 1 - Chân trời sáng tạo. Để giải quyết các bài tập này, học sinh có thể tham khảo các phương pháp sau:
Khi giải bài tập về giới hạn hàm số, học sinh cần lưu ý những điều sau:
Bài tập 8 trang 51 SGK Toán 12 tập 1 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về giới hạn hàm số. Hy vọng rằng với lời giải chi tiết và các phương pháp giải được trình bày trong bài viết này, các bạn học sinh sẽ tự tin hơn khi giải quyết các bài tập tương tự.
Chúc các bạn học tập tốt!