Giải bài tập 10 trang 29 SGK Toán 12 tập 2 - Chân trời sáng tạo

Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12 tập 2. Bài viết này sẽ hướng dẫn bạn giải bài tập 10 trang 29 SGK Toán 12 tập 2 theo chương trình Chân trời sáng tạo.

Chúng tôi cam kết cung cấp nội dung chính xác, đầy đủ và giúp bạn nắm vững kiến thức Toán học.

Tốc độ chuyển động (v{rm{ }}left( {{rm{m/s}}} right)) của một ca nô trong khoảng thời gian 40 giây được thể hiện như hình dưới đây. Quãng đường đi được của ca nô trong khoảng thời gian này là: A. 400 m B. 350 m C. 310 m D. 200 m

Đề bài

Tốc độ chuyển động \(v{\rm{ }}\left( {{\rm{m/s}}} \right)\) của một ca nô trong khoảng thời gian 40 giây được thể hiện như hình 1. Quãng đường đi được của ca nô trong khoảng thời gian này là:

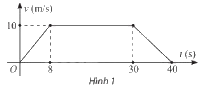
Giải bài tập 10 trang 29 SGK Toán 12 tập 2 - Chân trời sáng tạo 1

A. 400 m

B. 350 m

C. 310 m

D. 200 m

Phương pháp giải - Xem chi tiết Giải bài tập 10 trang 29 SGK Toán 12 tập 2 - Chân trời sáng tạo 2

Quãng đường đi được của ca nô trong khoảng thời gian 40 giây là \(s = \int\limits_0^{40} {v\left( t \right)dt} \).

Viết phương trình hàm \(v\left( t \right)\), sau đó tính tích phân \(s = \int\limits_0^{40} {v\left( t \right)dt} \).

Lời giải chi tiết

Đồ thị hàm số \(v\left( t \right)\) được chia thành 3 đường thằng \(OA\), \(AB\), \(BC\) như hình dưới đây.

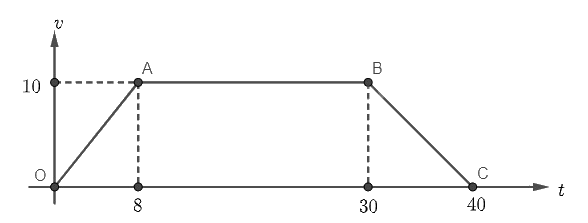
Giải bài tập 10 trang 29 SGK Toán 12 tập 2 - Chân trời sáng tạo 3

Đường thẳng \(OA\) đi qua \(O\left( {0;0} \right)\) và \(A\left( {8;10} \right)\) nên phương trình đường thẳng \(OA\) là \(v = \frac{5}{4}t\).

Đường thẳng \(AB\) đi qua \(A\left( {8;10} \right)\) và \(B\left( {30;10} \right)\) nên phương trình đường thẳng \(AB\) là \(v = 10\).

Đường thẳng \(BC\) đi qua \(B\left( {30;10} \right)\) và \(C\left( {40;0} \right)\) nên phương trình đường thẳng \(BC\) là \(v = - t + 40\).

Vậy \(v\left( t \right) = \left\{ \begin{array}{l}\frac{5}{4}t{\rm{ }}\left( {0 \le t \le 8} \right)\\10{\rm{ }}\left( {8 \le t \le 30} \right)\\ - t + 40{\rm{ }}\left( {30 \le t \le 40} \right)\end{array} \right.\).

Do đó, quãng đường ca nô đi được trong 40 giây là

\(s = \int\limits_0^{40} {v\left( t \right)dt} = \int\limits_0^8 {v\left( t \right)dt} + \int\limits_8^{30} {v\left( t \right)dt} + \int\limits_{30}^{40} {v\left( t \right)dt} = \int\limits_0^8 {\frac{5}{4}tdt} + \int\limits_8^{30} {10dt} + \int\limits_{30}^{40} {\left( { - t + 40} \right)dt} \)

\( = \frac{5}{4}\left. {\left( {\frac{{{t^2}}}{2}} \right)} \right|_0^8 + 10\left. {\left( t \right)} \right|_8^{30} + \left. {\left( { - \frac{{{t^2}}}{2} + 40t} \right)} \right|_{30}^{40} = \frac{5}{4}.32 + 10.22 + 50 = 310\) (m).

Đáp án đúng là C

Tự tin bứt phá Kỳ thi THPT Quốc gia môn Toán! Đừng bỏ lỡ Giải bài tập 10 trang 29 SGK Toán 12 tập 2 - Chân trời sáng tạo đặc sắc thuộc chuyên mục giải sgk toán 12 trên nền tảng soạn toán. Với bộ bài tập lý thuyết toán thpt được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình Toán 12, đây chính là "chiến lược vàng" giúp các em tối ưu hóa ôn luyện. Học sinh sẽ không chỉ làm chủ mọi dạng bài thi mà còn nắm vững chiến thuật làm bài hiệu quả, sẵn sàng tự tin chinh phục điểm cao, vững bước vào đại học mơ ước nhờ phương pháp học trực quan, khoa học và hiệu quả học tập vượt trội!

Giải bài tập 10 trang 29 SGK Toán 12 tập 2 - Chân trời sáng tạo: Tổng quan

Bài tập 10 trang 29 SGK Toán 12 tập 2 thuộc chương trình Chân trời sáng tạo, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế liên quan đến tốc độ thay đổi của một đại lượng. Bài tập này thường yêu cầu học sinh phải hiểu rõ các khái niệm như đạo hàm, quy tắc tính đạo hàm, và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.

Nội dung bài tập 10 trang 29 SGK Toán 12 tập 2 - Chân trời sáng tạo

Bài tập 10 thường bao gồm các dạng bài sau:

Dạng 1: Tính đạo hàm của hàm số: Yêu cầu tính đạo hàm của một hàm số cho trước, có thể là hàm số đơn giản hoặc hàm số phức tạp.
Dạng 2: Tìm cực trị của hàm số: Yêu cầu tìm điểm cực đại, điểm cực tiểu của hàm số bằng cách giải phương trình đạo hàm bằng 0 và xét dấu đạo hàm.
Dạng 3: Khảo sát sự biến thiên của hàm số: Yêu cầu xác định khoảng đồng biến, khoảng nghịch biến của hàm số dựa vào dấu của đạo hàm.
Dạng 4: Ứng dụng đạo hàm để giải quyết bài toán thực tế: Yêu cầu sử dụng đạo hàm để giải quyết các bài toán liên quan đến tốc độ thay đổi, tối ưu hóa, hoặc các bài toán vật lý.

Lời giải chi tiết bài tập 10 trang 29 SGK Toán 12 tập 2 - Chân trời sáng tạo

Để giúp các bạn học sinh giải quyết bài tập 10 trang 29 SGK Toán 12 tập 2 một cách hiệu quả, chúng tôi xin trình bày lời giải chi tiết cho từng dạng bài:

Ví dụ 1: Tính đạo hàm của hàm số f(x) = x³ - 2x² + 5x - 1

Lời giải:

f'(x) = 3x² - 4x + 5

Ví dụ 2: Tìm cực trị của hàm số g(x) = x⁴ - 4x² + 3

Lời giải:

g'(x) = 4x³ - 8x

Giải phương trình g'(x) = 0, ta được x = 0, x = √2, x = -√2

Xét dấu g'(x), ta thấy:

x < -√2: g'(x) < 0 (hàm số nghịch biến)
-√2 < x < 0: g'(x) > 0 (hàm số đồng biến)
0 < x < √2: g'(x) < 0 (hàm số nghịch biến)
x > √2: g'(x) > 0 (hàm số đồng biến)

Vậy hàm số đạt cực đại tại x = -√2 và x = √2, đạt cực tiểu tại x = 0.

Ví dụ 3: Khảo sát sự biến thiên của hàm số h(x) = x² - 6x + 9

Lời giải:

h'(x) = 2x - 6

Giải phương trình h'(x) = 0, ta được x = 3

Xét dấu h'(x), ta thấy:

x < 3: h'(x) < 0 (hàm số nghịch biến)
x > 3: h'(x) > 0 (hàm số đồng biến)

Vậy hàm số nghịch biến trên khoảng (-∞, 3) và đồng biến trên khoảng (3, +∞).

Mẹo giải bài tập đạo hàm hiệu quả

Để giải các bài tập về đạo hàm một cách hiệu quả, bạn nên:

Nắm vững các công thức tính đạo hàm cơ bản.
Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
Sử dụng các công cụ hỗ trợ như máy tính bỏ túi hoặc phần mềm giải toán.
Kiểm tra lại kết quả sau khi giải xong.

Kết luận

Hy vọng rằng với lời giải chi tiết và các mẹo giải bài tập trên, các bạn học sinh sẽ tự tin hơn khi giải bài tập 10 trang 29 SGK Toán 12 tập 2 - Chân trời sáng tạo. Chúc các bạn học tập tốt!