Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập Toán 12 tập 2. Bài viết này sẽ hướng dẫn bạn giải bài tập 5 trang 27 SGK Toán 12 tập 2 theo chương trình Chân trời sáng tạo.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi đã biên soạn lời giải một cách dễ hiểu, kèm theo các bước giải chi tiết để giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
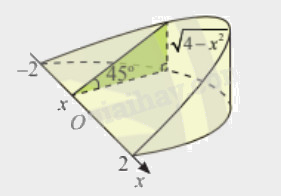
Khi cắt một vật thể hình chiếc nêm bởi mặt phẳng vuông góc với trục (Ox) tại điểm có hoành độ (x) (left( { - 2 le x le 2} right)), mặt cắt là tam giác vuông có một góc ({45^o}) và độ dài một cạnh góc vuông là (sqrt {4 - {x^2}} ) (dm). Tính thể tích của vật thể.
Đề bài
Khi cắt một vật thể hình chiếc nêm bởi mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ \(x\) \(\left( { - 2 \le x \le 2} \right)\), mặt cắt là tam giác vuông có một góc \({45^o}\) và độ dài một cạnh góc vuông là \(\sqrt {4 - {x^2}} \) (dm). Tính thể tích của vật thể.
Phương pháp giải - Xem chi tiết
Tính diện tích mặt cắt \(S\left( x \right)\), sau đó tính thể tích vật thể bằng công thức \(V = \int\limits_a^b {S\left( x \right)dx} \).
Lời giải chi tiết
Vì mặt cắt là một tam giác vuông có một góc \({45^o}\), nên mặt cắt là tam giác vuông cân. Do đó diện tích mặt cắt là \(S\left( x \right) = \frac{{{{\left( {\sqrt {4 - {x^2}} } \right)}^2}}}{2} = \frac{{4 - {x^2}}}{2}\).
Thể tích vật thể là:
\(V = \int\limits_{ - 2}^2 {\frac{{4 - {x^2}}}{2}dx} = \frac{1}{2}\int\limits_{ - 2}^2 {\left( {4 - {x^2}} \right)dx} = \frac{1}{2}\left. {\left( {4x - \frac{{{x^3}}}{3}} \right)} \right|_{ - 2}^2 = \frac{{16}}{3}\)
Bài tập 5 trang 27 SGK Toán 12 tập 2 thuộc chương trình Chân trời sáng tạo tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế liên quan đến tốc độ thay đổi của một đại lượng. Bài tập này thường yêu cầu học sinh phải hiểu rõ các khái niệm như đạo hàm, quy tắc tính đạo hàm, và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.
Bài tập 5 thường bao gồm các dạng bài sau:
Để giúp bạn hiểu rõ hơn về cách giải bài tập 5 trang 27, chúng tôi sẽ trình bày lời giải chi tiết cho từng dạng bài:
Ví dụ: Tính đạo hàm của hàm số f(x) = x3 + 2x2 - 5x + 1.
Lời giải:
f'(x) = 3x2 + 4x - 5
Ví dụ: Tìm cực trị của hàm số f(x) = x3 - 3x2 + 2.
Lời giải:
Ví dụ: Khảo sát sự biến thiên của hàm số f(x) = x4 - 4x2 + 3.
Lời giải:
(Tương tự như dạng 2, cần tính đạo hàm, giải phương trình đạo hàm bằng 0, xét dấu đạo hàm và kết luận khoảng đồng biến, nghịch biến)
Ví dụ: Một vật chuyển động với vận tốc v(t) = 3t2 - 6t + 2 (m/s). Tính gia tốc của vật tại thời điểm t = 2s.
Lời giải:
Gia tốc a(t) là đạo hàm của vận tốc v(t): a(t) = v'(t) = 6t - 6
Tại t = 2s: a(2) = 6(2) - 6 = 6 (m/s2)
Hy vọng rằng với lời giải chi tiết và các mẹo giải bài tập trên, bạn đã có thể tự tin giải quyết bài tập 5 trang 27 SGK Toán 12 tập 2 - Chân trời sáng tạo. Chúc bạn học tập tốt!