Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 tập 1 của giaitoan.edu.vn. Chúng tôi xin giới thiệu lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1, trang 68, 69, 70 sách giáo khoa Toán 12 tập 1 chương trình Chân trời sáng tạo.
Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi cam kết cung cấp những lời giải chính xác, đầy đủ và giúp các em nắm vững kiến thức.
Khoảng biến thiên
Trả lời câu hỏi Khám phá 1 trang 68 SGK Toán 12 Chân trời sáng tạo
Bảng sau thống kê cân nặng của 50 quả xoài Thanh Ca được lựa chọn ngẫu nhiên sau khi thu hoạch ở một nông trường.

Có ý kiến cho rằng: “Trong 50 quả xoài trên, hiệu số cân nặng của hai quả bất kì không vượt quá 200 g”. Ý kiến đó đúng hay sai? Giải thích.
Phương pháp giải:
Quan sát bảng số liệu
Lời giải chi tiết:
Ý kiến đó đúng. Vì: ta thấy trong bảng số liệu, cân nặng lớn nhất quả xoài có thể đạt được là 450g, còn cân nặng bé nhất quả xoài có thể đạt được là 250g. Do đó, bất kì hai quả nào cũng có hiệu số cân nặng không vượt quá 200g
Trả lời câu hỏi Thực hành 1 trang 70 SGK Toán 12 Chân trời sáng tạo
Bạn Trang thống kê lại chiều cao (đơn vị: cm) của các bạn học sinh nữ lớp 12C và lớp 12D ở bảng sau.
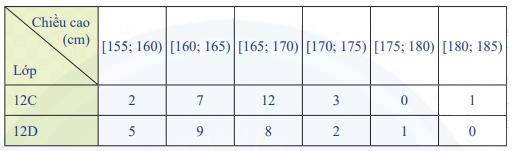
Nếu so sánh theo khoảng biến thiên thì chiều cao của học sinh lớp nào có độ phân tán lớn hơn?
Phương pháp giải:
Khoảng biến thiên của mẫu số liệu ghép nhóm là hiệu số giữa đầu mút phải của nhóm cuối cùng và đầu mút trái của nhóm đầu tiên có chứa dữ liệu của mẫu số liệu.
Lời giải chi tiết:
Khoảng biến thiên của chiều cao của các bạn học sinh nữ lớp 12C là: 185 – 155 = 30(cm)
Khoảng biến thiên của chiều cao của các bạn học sinh nữ lớp 12D là: 180 – 155 = 25(cm)
Vậy nếu so sánh theo khoảng biến thiên thì chiều cao của học sinh lớp 12C có độ phân tán lớn hơn
Trả lời câu hỏi Khám phá 1 trang 68 SGK Toán 12 Chân trời sáng tạo
Bảng sau thống kê cân nặng của 50 quả xoài Thanh Ca được lựa chọn ngẫu nhiên sau khi thu hoạch ở một nông trường.

Có ý kiến cho rằng: “Trong 50 quả xoài trên, hiệu số cân nặng của hai quả bất kì không vượt quá 200 g”. Ý kiến đó đúng hay sai? Giải thích.
Phương pháp giải:
Quan sát bảng số liệu
Lời giải chi tiết:
Ý kiến đó đúng. Vì: ta thấy trong bảng số liệu, cân nặng lớn nhất quả xoài có thể đạt được là 450g, còn cân nặng bé nhất quả xoài có thể đạt được là 250g. Do đó, bất kì hai quả nào cũng có hiệu số cân nặng không vượt quá 200g
Trả lời câu hỏi Thực hành 1 trang 70 SGK Toán 12 Chân trời sáng tạo
Bạn Trang thống kê lại chiều cao (đơn vị: cm) của các bạn học sinh nữ lớp 12C và lớp 12D ở bảng sau.
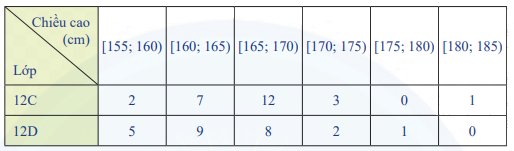
Nếu so sánh theo khoảng biến thiên thì chiều cao của học sinh lớp nào có độ phân tán lớn hơn?
Phương pháp giải:
Khoảng biến thiên của mẫu số liệu ghép nhóm là hiệu số giữa đầu mút phải của nhóm cuối cùng và đầu mút trái của nhóm đầu tiên có chứa dữ liệu của mẫu số liệu.
Lời giải chi tiết:
Khoảng biến thiên của chiều cao của các bạn học sinh nữ lớp 12C là: 185 – 155 = 30(cm)
Khoảng biến thiên của chiều cao của các bạn học sinh nữ lớp 12D là: 180 – 155 = 25(cm)
Vậy nếu so sánh theo khoảng biến thiên thì chiều cao của học sinh lớp 12C có độ phân tán lớn hơn
Mục 1 của chương trình Toán 12 tập 1 Chân trời sáng tạo tập trung vào việc ôn tập và mở rộng kiến thức về giới hạn. Đây là nền tảng quan trọng để học sinh tiếp cận các khái niệm phức tạp hơn trong chương trình. Việc giải các bài tập trong SGK là cách tốt nhất để củng cố kiến thức và rèn luyện kỹ năng giải toán.
Bài tập này yêu cầu học sinh vận dụng định nghĩa giới hạn của hàm số để tính giới hạn tại một điểm. Các em cần nắm vững các bước sau:
Ví dụ, để tính giới hạn của hàm số f(x) = (x^2 - 1)/(x - 1) tại x = 1, ta có thể rút gọn hàm số thành f(x) = x + 1, sau đó thay x = 1 vào để được giới hạn là 2.
Bài tập này yêu cầu học sinh tính giới hạn của hàm số khi x tiến tới vô cực hoặc trừ vô cực. Các em cần nắm vững các quy tắc tính giới hạn của hàm đa thức, hàm phân thức và các hàm số khác.
Ví dụ, để tính giới hạn của hàm số f(x) = (2x^2 + 1)/(x^2 + 3) khi x tiến tới vô cực, ta có thể chia cả tử và mẫu cho x^2 để được f(x) = (2 + 1/x^2)/(1 + 3/x^2). Khi x tiến tới vô cực, 1/x^2 và 3/x^2 tiến tới 0, do đó giới hạn của f(x) là 2.
Bài tập này yêu cầu học sinh sử dụng khái niệm giới hạn để tính đạo hàm của hàm số tại một điểm. Đạo hàm là một khái niệm quan trọng trong giải tích, được sử dụng để nghiên cứu sự thay đổi của hàm số.
Ví dụ, để tính đạo hàm của hàm số f(x) = x^2 tại x = 2, ta có thể sử dụng công thức đạo hàm: f'(x) = 2x. Thay x = 2 vào, ta được f'(2) = 4.
Ngoài SGK Toán 12 tập 1 Chân trời sáng tạo, các em có thể tham khảo thêm các tài liệu sau:
Hy vọng với lời giải chi tiết và những lưu ý trên, các em học sinh sẽ tự tin giải các bài tập trong mục 1 trang 68, 69, 70 SGK Toán 12 tập 1 Chân trời sáng tạo. Chúc các em học tập tốt!