Giải bài tập 2 trang 42 SGK Toán 12 tập 2 - Chân trời sáng tạo

Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập Toán 12 tập 2 theo chương trình Chân trời sáng tạo. Bài viết này sẽ giúp bạn hiểu rõ cách giải bài tập 2 trang 42, từ đó nắm vững kiến thức và tự tin hơn trong quá trình học tập.

Chúng tôi luôn cố gắng trình bày lời giải một cách dễ hiểu, logic, kèm theo các ví dụ minh họa cụ thể để bạn có thể áp dụng vào các bài tập tương tự.

a) Lập phương trình của các mặt phẳng toạ độ \(\left( {Oxy} \right)\), \(\left( {Oyz} \right)\), \(\left( {Oxz} \right)\). b) Lập phương trình của các mặt phẳng đi qua điểm \(A\left( { - 1;9;8} \right)\) và lần lượt song song với các mặt phẳng toạ độ trên.

Đề bài

a) Lập phương trình của các mặt phẳng toạ độ \(\left( {Oxy} \right)\), \(\left( {Oyz} \right)\), \(\left( {Oxz} \right)\).

b) Lập phương trình của các mặt phẳng đi qua điểm \(A\left( { - 1;9;8} \right)\) và lần lượt song song với các mặt phẳng toạ độ trên.

Phương pháp giải - Xem chi tiết Giải bài tập 2 trang 42 SGK Toán 12 tập 2 - Chân trời sáng tạo 1

a) Xác định một điểm đi qua và một vectơ pháp tuyến lần lượt của các mặt phẳng \(\left( {Oxy} \right)\), \(\left( {Oyz} \right)\), \(\left( {Oxz} \right)\).

b) Các mặt phẳng \(\left( P \right)\), \(\left( Q \right)\), \(\left( R \right)\) đi qua \(A\left( { - 1;9;8} \right)\) và lần lượt song song với các mặt phẳng toạ độ \(\left( {Oxy} \right)\), \(\left( {Oyz} \right)\), \(\left( {Oxz} \right)\) nên sẽ có các vectơ pháp tuyến theo thứ tự là vectơ pháp tuyến của \(\left( {Oxy} \right)\), \(\left( {Oyz} \right)\), \(\left( {Oxz} \right)\)

Lời giải chi tiết

a) Các mặt phẳng toạ độ \(\left( {Oxy} \right)\), \(\left( {Oyz} \right)\), \(\left( {Oxz} \right)\) đều đi qua điểm \(O\left( {0;0;0} \right)\).

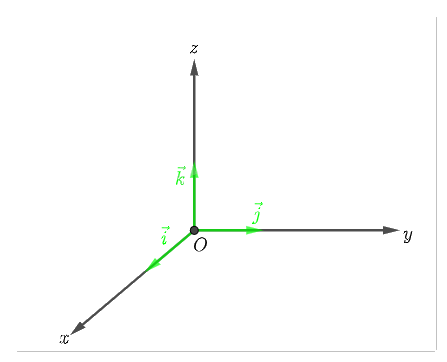
Giải bài tập 2 trang 42 SGK Toán 12 tập 2 - Chân trời sáng tạo 2

Mặt phẳng \(\left( {Oxy} \right)\) có một vectơ pháp tuyến là \(\vec k = \left( {0;0;1} \right)\) nên phương trình mặt phẳng \(\left( {Oxy} \right)\) là \(0\left( {x - 0} \right) + 0\left( {y - 0} \right) + 1\left( {z - 0} \right) = 0 \Leftrightarrow z = 0\).

Mặt phẳng \(\left( {Oyz} \right)\) có một vectơ pháp tuyến là \(\vec i = \left( {1;0;0} \right)\) nên phương trình mặt phẳng \(\left( {Oyz} \right)\) là \(1\left( {x - 0} \right) + 0\left( {y - 0} \right) + 0\left( {z - 0} \right) = 0 \Leftrightarrow x = 0\).

Mặt phẳng \(\left( {Oxz} \right)\) có một vectơ pháp tuyến là \(\vec j = \left( {0;1;0} \right)\) nên phương trình mặt phẳng \(\left( {Oxz} \right)\) là \(0\left( {x - 0} \right) + 1\left( {y - 0} \right) + 0\left( {z - 0} \right) = 0 \Leftrightarrow y = 0\)

b) Gọi \(\left( P \right)\), \(\left( Q \right)\), \(\left( R \right)\) đi qua \(A\left( { - 1;9;8} \right)\) và lần lượt song song với các mặt phẳng toạ độ \(\left( {Oxy} \right)\), \(\left( {Oyz} \right)\), \(\left( {Oxz} \right)\).

Mặt phẳng \(\left( P \right)\) song song với \(\left( {Oxy} \right)\), nên \(\left( P \right)\) có một vectơ pháp tuyến là \(\vec k = \left( {0;0;1} \right)\). Phương trình mặt phẳng \(\left( P \right)\) là \(0\left( {x + 1} \right) + 0\left( {y - 9} \right) + 1\left( {z - 8} \right) = 0 \Leftrightarrow z - 8 = 0\)

Mặt phẳng \(\left( Q \right)\) song song với \(\left( {Oyz} \right)\), nên \(\left( Q \right)\) có một vectơ pháp tuyến là \(\vec i = \left( {1;0;0} \right)\). Phương trình mặt phẳng \(\left( Q \right)\) là \(1\left( {x + 1} \right) + 0\left( {y - 9} \right) + 0\left( {z - 8} \right) = 0 \Leftrightarrow x + 1 = 0\)

Mặt phẳng \(\left( R \right)\) song song với \(\left( {Oxy} \right)\), nên \(\left( R \right)\) có một vectơ pháp tuyến là \(\vec j = \left( {0;1;0} \right)\). Phương trình mặt phẳng \(\left( R \right)\) là \(0\left( {x + 1} \right) + 1\left( {y - 9} \right) + 0\left( {z - 8} \right) = 0 \Leftrightarrow y - 9 = 0\)

Tự tin bứt phá Kỳ thi THPT Quốc gia môn Toán! Đừng bỏ lỡ Giải bài tập 2 trang 42 SGK Toán 12 tập 2 - Chân trời sáng tạo đặc sắc thuộc chuyên mục toán lớp 12 trên nền tảng toán math. Với bộ bài tập lý thuyết toán thpt được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình Toán 12, đây chính là "chiến lược vàng" giúp các em tối ưu hóa ôn luyện. Học sinh sẽ không chỉ làm chủ mọi dạng bài thi mà còn nắm vững chiến thuật làm bài hiệu quả, sẵn sàng tự tin chinh phục điểm cao, vững bước vào đại học mơ ước nhờ phương pháp học trực quan, khoa học và hiệu quả học tập vượt trội!

Giải bài tập 2 trang 42 SGK Toán 12 tập 2 - Chân trời sáng tạo: Tổng quan

Bài tập 2 trang 42 SGK Toán 12 tập 2 chương trình Chân trời sáng tạo thường xoay quanh các chủ đề về đạo hàm của hàm số, ứng dụng đạo hàm để khảo sát hàm số và giải các bài toán liên quan đến cực trị, giá trị lớn nhất, giá trị nhỏ nhất của hàm số. Việc nắm vững kiến thức về đạo hàm là nền tảng quan trọng để giải quyết bài tập này.

Phân tích đề bài và xác định yêu cầu

Trước khi bắt đầu giải bài tập, điều quan trọng nhất là phải đọc kỹ đề bài, xác định rõ yêu cầu của đề bài là gì. Ví dụ, đề bài yêu cầu tính đạo hàm, tìm cực trị, hay giải phương trình, bất phương trình. Việc xác định đúng yêu cầu sẽ giúp bạn lựa chọn phương pháp giải phù hợp.

Các bước giải bài tập 2 trang 42 SGK Toán 12 tập 2

Bước 1: Tính đạo hàm của hàm số. Sử dụng các quy tắc tính đạo hàm đã học để tính đạo hàm cấp một của hàm số.
Bước 2: Tìm tập xác định của hàm số. Xác định khoảng xác định của hàm số, loại bỏ các điểm mà hàm số không xác định.
Bước 3: Tìm các điểm tới hạn. Giải phương trình đạo hàm bằng 0 để tìm các điểm mà đạo hàm bằng 0 hoặc không xác định. Các điểm này được gọi là các điểm tới hạn.
Bước 4: Khảo sát dấu của đạo hàm. Lập bảng xét dấu của đạo hàm trên các khoảng xác định. Dựa vào dấu của đạo hàm, ta có thể xác định khoảng hàm số đồng biến, nghịch biến.
Bước 5: Xác định cực trị của hàm số. Dựa vào bảng xét dấu của đạo hàm, ta có thể xác định các điểm cực đại, cực tiểu của hàm số.
Bước 6: Giải quyết yêu cầu của đề bài. Dựa vào kết quả đã tìm được, giải quyết yêu cầu của đề bài, ví dụ như tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số.

Ví dụ minh họa

Giả sử đề bài yêu cầu tìm cực trị của hàm số y = x³ - 3x² + 2.

Tính đạo hàm: y' = 3x² - 6x
Tìm tập xác định: Hàm số xác định trên R.
Tìm điểm tới hạn: 3x² - 6x = 0 => x = 0 hoặc x = 2
Khảo sát dấu của đạo hàm:
x -∞ 0 2 +∞
y' + - +
y NB ĐB NT
Xác định cực trị: Hàm số đạt cực đại tại x = 0, y_CĐ = 2. Hàm số đạt cực tiểu tại x = 2, y_CT = -2.

x	-∞	0	2	+∞
y'	+	-	+
y	NB	ĐB	NT

Lưu ý khi giải bài tập

Luôn kiểm tra lại kết quả sau khi giải bài tập.
Sử dụng máy tính cầm tay để kiểm tra lại các phép tính.
Tham khảo các tài liệu tham khảo khác để hiểu rõ hơn về kiến thức.
Luyện tập thường xuyên để nâng cao kỹ năng giải bài tập.

Ứng dụng của đạo hàm trong thực tế

Đạo hàm có rất nhiều ứng dụng trong thực tế, ví dụ như trong vật lý, đạo hàm được sử dụng để tính vận tốc, gia tốc. Trong kinh tế, đạo hàm được sử dụng để tính chi phí biên, doanh thu biên. Trong kỹ thuật, đạo hàm được sử dụng để tối ưu hóa các thiết kế.

Kết luận

Bài tập 2 trang 42 SGK Toán 12 tập 2 chương trình Chân trời sáng tạo là một bài tập quan trọng giúp bạn củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm. Hy vọng với hướng dẫn chi tiết này, bạn sẽ tự tin hơn trong quá trình giải bài tập và đạt kết quả tốt trong môn Toán.