Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài tập 12 trang 60 SGK Toán 12 tập 2 - Chân trời sáng tạo. Bài viết này cung cấp phương pháp giải bài tập, đáp án chính xác và giải thích rõ ràng từng bước để giúp học sinh hiểu sâu kiến thức Toán học.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, hỗ trợ học sinh ôn tập và làm bài tập hiệu quả. Hãy cùng giaitoan.edu.vn khám phá lời giải bài tập này ngay nhé!
Trong không gian (Oxyz), cho hình lăng trụ đứng (OBC.O'B'C') có đáy là tam giác (OBC) vuông tại (O). Cho biết (Bleft( {3;0;0} right)), (Cleft( {0;1;0} right)), (O'left( {0;0;2} right)). Tính góc giữa: a) hai đường thẳng (BO') và (B'C). b) hai mặt phẳng (left( {O'BC} right)) và (left( {OBC} right)). c) đường thẳng (B'C) và mặt phẳng (left( {O'BC} right)).
Đề bài
Trong không gian Oxyz, cho hình lăng trụ đứng OBC.O'B'C' có đáy là tam giác OBC vuông tại O. Cho biết B(3;0;0), C(0;1;0), O'(0;0;2). Tính góc giữa:
a) Hai đường thẳng BO' và B'C.
b) Hai mặt phẳng (O'BC) và (OBC).
c) Đường thẳng B'C và mặt phẳng (O'BC).
Phương pháp giải - Xem chi tiết
a) Chỉ ra \(\overrightarrow {BO'} \) và \(\overrightarrow {B'C} \) lần lượt là các vectơ chỉ phương của các đường thẳng \(BO'\) và \(B'C\), sau đó sử dụng công thức \(\cos \left( {BO',B'C} \right) = \left| {\cos \left( {\overrightarrow {BO} ',\overrightarrow {B'C} } \right)} \right|\).
b) Với mặt phẳng \(\left( {O'BC} \right)\), ta cần chỉ ra một cặp vectơ chỉ phương, rồi tính tích có hướng để lần lượt tìm ra vectơ pháp tuyến \(\vec n\).
Với mặt phẳng \(\left( {OBC} \right)\), chỉ ra rằng \(\overrightarrow {OO'} \) là một vectơ pháp tuyến của mặt phẳng đó.
Từ đó suy ra \(\cos \left( {\left( {O'BC} \right),\left( {OBC} \right)} \right) = \left| {\cos \left( {\overrightarrow {OO'} ,\vec n} \right)} \right|\).
c) Từ câu a và b, ta có \(\overrightarrow {B'C} \) là một vectơ chỉ phương của \(B'C\), \(\vec n\) là một vectơ pháp tuyến của mặt phẳng \(\left( {O'BC} \right)\). Suy ra \(\sin \left( {B'C,\left( {O'BC} \right)} \right) = \left| {\cos \left( {\overrightarrow {B'C} ,\vec n} \right)} \right|\).
Lời giải chi tiết
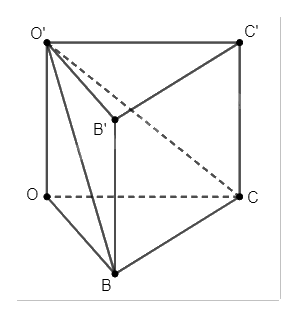
a) Ta có toạ độ các điểm \(O\left( {0;0;0} \right)\), \(B\left( {3;0;0} \right)\), \(C\left( {0;1;0} \right)\), \(O'\left( {0;0;2} \right)\). Suy ra \(B'\left( {3;0;2} \right)\).
Ta có \(\overrightarrow {BO'} = \left( { - 3;0;2} \right)\) là một vectơ chỉ phương của đường thẳng \(BO'\) và \(\overrightarrow {B'C} = \left( { - 3;1; - 2} \right)\) là một vectơ chỉ phương của đường thẳng \(B'C\). Suy ra:
\(\cos \left( {BO',B'C} \right) = \left| {\cos \left( {\overrightarrow {BO} ',\overrightarrow {B'C} } \right)} \right| = \frac{{\left| {\left( { - 3} \right).\left( { - 3} \right) + 0.1 + 2.\left( { - 2} \right)} \right|}}{{\sqrt {{{\left( { - 3} \right)}^2} + {0^2} + {2^2}} .\sqrt {{{\left( { - 3} \right)}^2} + {1^2} + {{\left( { - 2} \right)}^2}} }} = \frac{5}{{\sqrt {182} }}\)
Từ đó \(\left( {BO',B'C} \right) \approx {68^o}15'\).
b) Mặt phẳng \(\left( {O'BC} \right)\) có cặp vectơ chỉ phương là \(\overrightarrow {BC} = \left( { - 3;1;0} \right)\) và \(\overrightarrow {BO'} = \left( { - 3;0;2} \right)\). Suy ra một vectơ pháp tuyến của \(\left( {O'BC} \right)\) là \(\vec n = \left[ {\overrightarrow {BC} ,\overrightarrow {BO'} } \right] = \left( {2;6;3} \right)\).
Mặt phẳng \(\left( {OBC} \right)\) có \(OO' \bot \left( {OBC} \right)\) nên \(\overrightarrow {OO'} = \left( {0;0;2} \right)\) là một vectơ pháp tuyến của \(\left( {OBC} \right)\).
Suy ra
\(\cos \left( {\left( {O'BC} \right),\left( {OBC} \right)} \right) = \left| {\cos \left( {\overrightarrow {OO'} ,\vec n} \right)} \right| = \frac{{\left| {2.0 + 6.0 + 3.2} \right|}}{{\sqrt {{2^2} + {6^2} + {3^2}} .\sqrt {{0^2} + {0^2} + {2^2}} }} = \frac{3}{7}\).
Vậy \(\left( {\left( {O'BC} \right),\left( {OBC} \right)} \right) \approx {64^o}37'\).
c) Ta có \(\overrightarrow {B'C} = \left( { - 3;1; - 2} \right)\) là một vectơ chỉ phương của đường thẳng \(B'C\).
Ta có \(\vec n = \left( {2;6;3} \right)\) là một vectơ pháp tuyến của mặt phẳng \(\left( {O'BC} \right)\). Suy ra
\(\sin \left( {B'C,\left( {O'BC} \right)} \right) = \left| {\cos \left( {\overrightarrow {B'C} ,\vec n} \right)} \right| = \frac{{\left| {\left( { - 3} \right).2 + 1.6 + \left( { - 2} \right).3} \right|}}{{\sqrt {{{\left( { - 3} \right)}^2} + {1^2} + {{\left( { - 2} \right)}^2}} .\sqrt {{2^2} + {6^2} + {3^2}} }} = \frac{{3\sqrt {14} }}{{49}}\)
Vậy \(\left( {B'C,\left( {O'BC} \right)} \right) \approx {13^o}15'\).
Bài tập 12 trang 60 SGK Toán 12 tập 2 - Chân trời sáng tạo thuộc chương trình học Toán 12, tập trung vào kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Bài tập 12 thường xoay quanh các chủ đề sau:
Để giải quyết bài tập 12 trang 60 SGK Toán 12 tập 2 - Chân trời sáng tạo một cách hiệu quả, học sinh cần nắm vững các bước sau:
Bài tập: Cho hàm số y = x3 - 3x2 + 2. Tìm khoảng đồng biến của hàm số.
Giải:
Để đạt kết quả tốt nhất khi giải bài tập 12 trang 60 SGK Toán 12 tập 2 - Chân trời sáng tạo, học sinh cần:
Giaitoan.edu.vn là địa chỉ tin cậy dành cho học sinh, sinh viên và những người yêu thích môn Toán. Chúng tôi cung cấp:
Hãy truy cập giaitoan.edu.vn ngay hôm nay để khám phá thêm nhiều tài liệu học tập hữu ích và nâng cao kiến thức Toán học của bạn!
| Hàm số y | Đạo hàm y' |
|---|---|
| y = c (hằng số) | y' = 0 |
| y = xn | y' = nxn-1 |
| y = sinx | y' = cosx |
| y = cosx | y' = -sinx |