Chào mừng các em học sinh đến với lời giải chi tiết bài 10 trang 90 Sách bài tập Toán 8 Cánh Diều. Bài viết này sẽ cung cấp đáp án, phương pháp giải và giải thích rõ ràng từng bước để giúp các em hiểu bài và làm bài tập một cách hiệu quả.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán, cung cấp tài liệu học tập chất lượng và hỗ trợ giải đáp mọi thắc mắc.
Thả diều là một trò chơi dân gian của nhiều trẻ em ở Việt Nam cũng như ở nhiều nước trên thế giới.
Đề bài
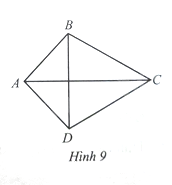
Thả diều là một trò chơi dân gian của nhiều trẻ em ở Việt Nam cũng như ở nhiều nước trên thế giới. Một tứ giác \(ABCD\) với \(AB = AD,BC = CD\) gọi là hình “chiếc diều” (Hình 9)
a) So sánh \(\widehat B\) và \(\widehat D\).
b) Tìm mối liên hệ giữa hai đường chéo \(AC\) và \(BD\)
Phương pháp giải - Xem chi tiết
Áp dụng các trường hợp bằng nhau của tam giác để tìm các góc bằng nhau tương ứng.
Lời giải chi tiết
Gọi \(O\) là giao điểm của hai đường chéo \(AC\) và \(BD\)
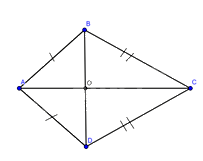
a) \(\Delta ABC = \Delta ADC\) (c-c-c). suy ra \(\widehat {ABC} = \widehat {ADC}\)
b) \(\Delta ABC = \Delta ADC\) nên \(\widehat {BAO} = \widehat {DAO}\)
\(\Delta ABO = \Delta ADo\). Suy ra \(\widehat {AOB} = \widehat {AOD}\)
Mà \(\widehat {AOD} + \widehat {AOB} = 180^\circ \) nên \(\widehat {AOB} = \widehat {AOD} = 90^\circ \)
Vậy \(AC \bot BD\).
Bài 10 trang 90 Sách bài tập Toán 8 Cánh Diều thuộc chương trình học Toán 8, tập trung vào việc vận dụng các kiến thức đã học về hình học, cụ thể là các tính chất của hình thang cân để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh phải nắm vững các định lý, tính chất liên quan đến hình thang cân, đồng thời rèn luyện kỹ năng phân tích đề bài, lập luận logic và trình bày lời giải một cách rõ ràng, mạch lạc.
Bài 10 bao gồm một số câu hỏi nhỏ, yêu cầu học sinh thực hiện các thao tác như:
Để xác định các yếu tố của hình thang cân, học sinh cần dựa vào định nghĩa và các tính chất của hình thang cân. Ví dụ, nếu một tứ giác có hai cạnh song song và hai cạnh bên bằng nhau thì đó là hình thang cân. Học sinh cần phân tích kỹ đề bài để xác định các yếu tố đã cho và từ đó suy ra các yếu tố còn lại.
Để tính độ dài các cạnh, đường cao của hình thang cân, học sinh có thể sử dụng các định lý và công thức liên quan. Ví dụ, độ dài đường trung bình của hình thang cân bằng nửa tổng độ dài hai đáy. Đường cao của hình thang cân có thể được tính bằng cách sử dụng định lý Pitago trong tam giác vuông tạo bởi đường cao, cạnh bên và một phần của đáy lớn.
Để chứng minh một tứ giác là hình thang cân, học sinh cần chứng minh tứ giác đó có hai cạnh song song và hai cạnh bên bằng nhau. Có thể sử dụng các định lý về tam giác đồng dạng, tam giác bằng nhau để chứng minh hai cạnh bên bằng nhau.
Ví dụ: Cho hình thang cân ABCD (AB // CD), AB = 5cm, CD = 10cm, AD = BC = 6cm. Tính đường cao AH của hình thang.
Giải:
Để học tốt môn Toán 8, các em có thể tham khảo thêm các tài liệu sau:
Bài 10 trang 90 Sách bài tập Toán 8 Cánh Diều là một bài tập quan trọng giúp các em củng cố kiến thức về hình thang cân. Hy vọng với lời giải chi tiết và hướng dẫn giải bài tập trên, các em sẽ tự tin hơn trong việc giải quyết các bài toán tương tự. Chúc các em học tập tốt!