Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài 34 trang 64 sách bài tập Toán 8 Cánh Diều. Bài viết này sẽ giúp bạn nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi luôn cố gắng trình bày lời giải một cách rõ ràng, logic, kèm theo các ví dụ minh họa để bạn dễ dàng tiếp thu và áp dụng vào thực tế.
Cho hai hàm số \(y = x + 5;y = - x + 1\).
Đề bài
Cho hai hàm số \(y = x + 5;y = - x + 1\).
a) Vẽ đồ thị của hai hàm số đó trên cùng một mặt phẳng tọa độ.
b) Gọi \(A\) là giao điểm của hai đường thẳng \(y = x + 5;y = - x + 1\); \(B,C\) lần lượt là giao điểm của hai đường thẳng đó với trục \(Ox\). Tính diện tích của tam giác \(ABC\) (đơn vị đo trên các trục tọa độ là centimet).
Phương pháp giải - Xem chi tiết
Vẽ đồ thị của hai hàm số trên cùng một mặt phẳng tọa độ và áp dụng công thức tính diện tích của tam giác để tính diện tích của tam giác \(ABC\) (đơn vị đo trên các trục tọa độ là centimet).
Lời giải chi tiết
Xét đồ thị hàm số \(y = x + 5\), ta có:
Chọn \(x = 0\) suy ra \(y = 5\)
Chọn \(y = 0\) suy ra \(x = - 5\)
Vậy đồ thị của hàm số \(y = x + 5\) là đường thẳng đi qua hai điểm \(A\left( {0;5} \right),B\left( { - 5;0} \right)\).
Xét đồ thị hàm số \(y = - x + 1\), ta có:
Chọn \(x = 0\) suy ra \(y = 1\)
Chọn \(y = 0\) suy ra \(x = 1\).
Vậy đồ thị của hàm số \(y = - x + 1\) là đường thẳng đi qua hai điểm \(C\left( {0;1} \right)\), \(D\left( {1;0} \right)\)
Vẽ đồ thị hàm số trên mặt phẳng tọa độ:
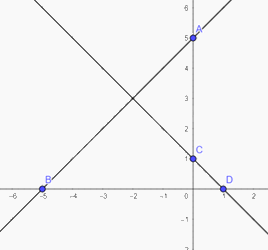
a) Gọi \(H\) là hình chiếu của \(E\) trên trục \(Ox\)
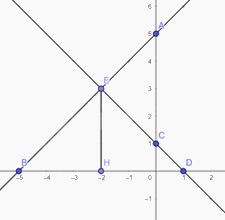
Ta có: \(E\left( { - 2;3} \right),B\left( { - 5;0} \right),C\left( {1;0} \right),H\left( { - 2;0} \right)\). Khi đó \(EH = 3cm\), \(BD = 6cm\)
Vậy diện tích của tam giác \(EBD\) là: \(\frac{1}{2}.3.6 = 9\left( {c{m^2}} \right)\).
Bài 34 trang 64 sách bài tập Toán 8 Cánh Diều thuộc chương trình học Toán 8, tập trung vào việc ôn tập và củng cố kiến thức về các dạng bài tập liên quan đến hình học, cụ thể là các tính chất của hình thang cân. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Bài 34 bao gồm một số câu hỏi và bài tập khác nhau, yêu cầu học sinh:
Một hình thang cân là một hình thang có hai cạnh đáy song song và hai cạnh bên bằng nhau. Các tính chất của hình thang cân bao gồm:
Để chứng minh một tứ giác là hình thang cân, ta cần chứng minh tứ giác đó là hình thang và hai cạnh bên bằng nhau. Ví dụ, nếu ta có tứ giác ABCD với AB song song CD và AD = BC, thì ABCD là hình thang cân.
Các phương pháp chứng minh thường được sử dụng bao gồm:
Để tính độ dài các cạnh của hình thang cân, ta có thể sử dụng các công thức và định lý liên quan đến hình thang cân. Ví dụ, nếu ta biết độ dài hai đáy và một cạnh bên, ta có thể sử dụng định lý Pitago để tính độ dài cạnh bên còn lại.
Ngoài ra, ta cũng có thể sử dụng các tính chất của hình thang cân để thiết lập các phương trình và giải phương trình để tìm ra độ dài các cạnh.
Kiến thức về hình thang cân có ứng dụng rộng rãi trong thực tế, đặc biệt trong các lĩnh vực như kiến trúc, xây dựng, thiết kế và đo đạc. Ví dụ, hình thang cân thường được sử dụng trong thiết kế mái nhà, cầu đường và các công trình xây dựng khác.
Để củng cố kiến thức về hình thang cân, bạn có thể luyện tập thêm các bài tập tương tự trong sách bài tập Toán 8 Cánh Diều hoặc các tài liệu tham khảo khác. Ngoài ra, bạn cũng có thể tìm kiếm các bài tập trực tuyến trên các trang web học Toán uy tín.
Bài 34 trang 64 sách bài tập Toán 8 Cánh Diều là một bài tập quan trọng giúp học sinh ôn tập và củng cố kiến thức về hình thang cân. Hy vọng rằng với lời giải chi tiết và các mẹo giải bài tập hiệu quả mà chúng tôi đã cung cấp, bạn sẽ tự tin hơn trong việc giải quyết các bài toán liên quan đến hình thang cân.