Bài 41 trang 75 sách bài tập Toán 8 Cánh Diều là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về các định lý, tính chất của hình học để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho bài 41 trang 75, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
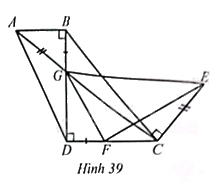
Hình thang (ABCD) ở Hình 39 có (AB//CD,AB < CD,widehat {ABD} = 90^circ ). Hai đường chéo (AC) và (BD) cắt nhau tại (G).
Đề bài
Hình thang \(ABCD\) ở Hình 39 có \(AB//CD,AB < CD,\widehat {ABD} = 90^\circ \). Hai đường chéo \(AC\) và \(BD\) cắt nhau tại \(G\). Điểm \(E\) nằm trên đường vuông góc với \(AC\) tại \(C\) thỏa mãn \(CE = AG\) và đoạn thẳng \(GE\) không cắt đường thẳng \(CD\). Điểm \(F\) nằm trên đoạn thẳng \(DC\) và \(DF = GB\). Chứng minh:
a) \(\Delta FGD\backsim \Delta ECG\);
b) \(\Delta GDC\backsim \Delta GFE\);
c) \(\widehat {GFE} = 90^\circ \).
Phương pháp giải - Xem chi tiết
Áp dụng trường hợp đồng dạng thứ hai của tam giác: cạnh – góc – cạnh
Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đó đồng dạng.
Lời giải chi tiết
a) Do \(AB//CD\) nên \(\frac{{BG}}{{AG}} = \frac{{GD}}{{GC}}\).
Mặt khác \(AG = CE,BG = DF\) nên \(\frac{{DF}}{{CE}} = \frac{{GD}}{{GC}}\).
Mà \(\widehat {GDF} = \widehat {GCE}\) nên \(\Delta FDG\backsim \Delta ECG\).
b) Vì \(\Delta FDG\backsim \Delta ECG\) nên \(\widehat {DGF} = \widehat {CGE}\) và \(\frac{{DG}}{{GF}} = \frac{{GC}}{{GE}}\).
\(\widehat {DGF} = \widehat {CGE} = > \widehat {DGF} + \widehat {FGC} = + \widehat {FGC}\).
Hay \(\widehat {DGC} = \widehat {FGE}\).
Từ đó, ta có \(\Delta GDC\backsim \Delta GFE\) vì \(\frac{DG}{GF}=\frac{GC}{GE}\) và \(\widehat{DGC}=\widehat{FGE}\).
c) Vì \(\Delta GDC\backsim \Delta GFE\) nên \(\widehat {GFE} = \widehat {GDC} = 90^\circ \).
Bài 41 trang 75 sách bài tập Toán 8 Cánh Diều thuộc chương trình học Toán 8, tập trung vào việc vận dụng các kiến thức về hình học, đặc biệt là các định lý liên quan đến tam giác đồng dạng và các tính chất của đường thẳng song song. Việc nắm vững kiến thức nền tảng và kỹ năng giải toán là yếu tố then chốt để giải quyết bài tập này một cách hiệu quả.
Trước khi bắt đầu giải bài, học sinh cần đọc kỹ đề bài, xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Thông thường, bài toán sẽ cung cấp một hình vẽ hoặc một mô tả về một tình huống hình học, và yêu cầu tính toán một độ dài, góc, diện tích hoặc chứng minh một mối quan hệ nào đó.
Để giải bài 41 trang 75, học sinh cần nắm vững các kiến thức sau:
(Ở đây sẽ là lời giải chi tiết của bài 41, bao gồm các bước giải, các phép tính và giải thích rõ ràng. Lời giải sẽ được trình bày một cách logic và dễ hiểu, kèm theo hình vẽ minh họa nếu cần thiết.)
Để giúp học sinh hiểu rõ hơn về cách giải bài 41, chúng ta sẽ xem xét một số ví dụ minh họa và bài tập tương tự:
(Giải thích chi tiết cách giải từng ví dụ, áp dụng các kiến thức đã học.)
Để giải các bài toán hình học một cách hiệu quả, học sinh nên lưu ý những điều sau:
Các kiến thức và kỹ năng giải toán trong bài 41 trang 75 có ứng dụng rộng rãi trong thực tế, ví dụ như trong kiến trúc, xây dựng, đo đạc, và các lĩnh vực kỹ thuật khác.
Bài 41 trang 75 sách bài tập Toán 8 Cánh Diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về hình học và rèn luyện kỹ năng giải toán. Hy vọng với hướng dẫn chi tiết và dễ hiểu trên đây, các em học sinh sẽ tự tin giải quyết bài tập này và đạt kết quả tốt trong môn Toán.
Lưu ý: Bài giải trên chỉ mang tính chất tham khảo. Học sinh nên tự mình giải bài tập để hiểu rõ hơn về kiến thức và rèn luyện kỹ năng giải toán.