Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 8 Cánh Diều. Bài viết này sẽ hướng dẫn bạn từng bước giải bài 13 trang 92, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, đồng thời giúp bạn hiểu rõ bản chất của từng bài toán.
Cho hình thang cân (ABCD) có (AB//CD,AB = 3mc,CD = 6cm,AD = 2.5cm). Gọi (M,N) lần lượt là hình chiếu của (A,B) trên đường thẳng (CD).
Đề bài
Cho hình thang cân \(ABCD\) có \(AB//CD,AB = 3mc,CD = 6cm,AD = 2.5cm\). Gọi \(M,N\) lần lượt là hình chiếu của \(A,B\) trên đường thẳng \(CD\). Tính độ dài các đoạn thẳng \(DM,DN,AM\).
Phương pháp giải - Xem chi tiết
Áp dụng các trường hợp bằng nhau của tam giác vuông và tính chất của hình thang cân để tính độ dài các đoạn thẳng \(DM,DN,AM\).
Lời giải chi tiết
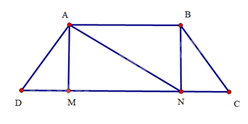
Xét tam giác ADM và tam giác ACM có:
AD = BC (vì ABCD là hình thang cân)
\(\widehat{D} = \widehat{C}\) (vì ABCD là hình thang cân)
Suy ra \(\Delta ADM = \Delta BCN\) (cạnh huyền – góc nhọn)
Do đó \(AM = BN;DM = CN\)
Xét tam giác ABN và tam giác NMA có:
AN chung
\(\widehat{BAN} = \widehat{MNA}\) (hai góc so le trong)
Suy ra \(\Delta ABN = \Delta NMA\) (cạnh huyền – góc nhọn)
nên \(AB = NM\). Do đó, \(NM = 3cm\)
Ta có: \(DM + NM + CN = CD\) và \(DM = CN\) nên \(2DM + 3 = 6\)
Suy ra \(DM = 1,5\)
Mà \(DN = DM + NM\), suy ra \(DN = 4,5cm\)
Trong tam giác \(ADM\) vuông tại \(M\), ta có:
\(A{D^2} = A{M^2} + D{M^2}\)
Suy ra \(A{M^2} = A{D^2} - D{M^2} = 4\).
Vậy \(AM = \sqrt 4 = 2\left( {cm} \right)\).
Bài 13 trang 92 sách bài tập Toán 8 Cánh Diều thuộc chương trình học Toán 8, tập trung vào việc vận dụng các kiến thức về hình học, cụ thể là các tính chất của hình thang cân. Bài tập này yêu cầu học sinh phải hiểu rõ các định nghĩa, định lý liên quan đến hình thang cân để có thể giải quyết một cách chính xác.
Bài 13 trang 92 sách bài tập Toán 8 Cánh Diều thường bao gồm các dạng bài tập sau:
Để giải bài 13 trang 92 sách bài tập Toán 8 Cánh Diều một cách hiệu quả, bạn cần thực hiện theo các bước sau:
Bài toán: Cho hình thang cân ABCD (AB // CD), AB = 6cm, CD = 10cm, AD = BC = 5cm. Tính chiều cao của hình thang.
Giải:
Kẻ AH và BK vuông góc với CD (H, K thuộc CD). Khi đó, AH = BK là chiều cao của hình thang.
Vì ABCD là hình thang cân nên DH = KC = (CD - AB) / 2 = (10 - 6) / 2 = 2cm.
Xét tam giác vuông ADH, ta có: AH2 = AD2 - DH2 = 52 - 22 = 21.
Vậy, AH = √21 cm. Do đó, chiều cao của hình thang ABCD là √21 cm.
Khi giải bài tập về hình thang cân, bạn cần lưu ý những điều sau:
Để củng cố kiến thức và kỹ năng giải bài tập về hình thang cân, bạn có thể tham khảo các bài tập sau:
Bài 13 trang 92 sách bài tập Toán 8 Cánh Diều là một bài tập quan trọng giúp bạn hiểu rõ hơn về hình thang cân và các tính chất của nó. Hy vọng rằng, với hướng dẫn chi tiết và ví dụ minh họa trong bài viết này, bạn sẽ tự tin hơn trong quá trình giải bài tập và học tập môn Toán 8.
Giaitoan.edu.vn luôn đồng hành cùng bạn trên con đường chinh phục kiến thức Toán học. Chúc bạn học tập tốt!