Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 8. Bài viết này sẽ hướng dẫn bạn giải bài 25 trang 97 sách bài tập Toán 8 - Cánh Diều một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, đặc biệt là với những bài tập đòi hỏi sự tư duy và vận dụng kiến thức. Vì vậy, chúng tôi luôn cố gắng cung cấp những lời giải rõ ràng, chi tiết, kèm theo các giải thích cụ thể để bạn có thể hiểu rõ bản chất của bài toán.
Cho tam giác \(ABC\) vuông cân tại \(A\). Lấy điểm \(M\) thuộc cạnh huyền \(BC\). Gọi \(D,E\) lần lượt là hình chiếu của điểm \(M\) trên đường thẳng \(AB,AC\).
Đề bài
Cho tam giác \(ABC\) vuông cân tại \(A\). Lấy điểm \(M\) thuộc cạnh huyền \(BC\). Gọi \(D,E\) lần lượt là hình chiếu của điểm \(M\) trên đường thẳng \(AB,AC\).
a) Tứ giác \(ADME\) là hình gì? Vì sao?
b) Gọi \(I\) là trung điểm của \(DE\). Chứng minh ba điểm \(A,I,M\) thẳng hàng
c) Chứng minh khi điểm \(M\) thay đổi vị trí trên cạnh \(BC\) thì chu vi của tứ giác \(ADME\) không đổi.
Phương pháp giải - Xem chi tiết
Dựa vào tính chất của hình chữ nhật:
- Hai cạnh đối song song và bằng nhau
- Hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường
Và dựa vào định lí Pythagore: trong một tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
Lời giải chi tiết
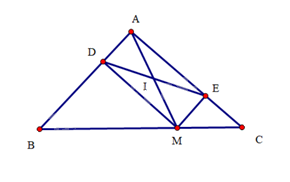
a) Tứ giác \(ADME\) có \(\widehat {DAE} = \widehat {AEM} = \widehat {MDA} = 90^\circ \) nên \(ADME\) là hình chữ nhật.
b) Do \(ADME\) là hình chữ nhật nên hai đường chéo \(DE\) và \(AM\) cắt nhau tại trung điểm của mỗi đường.
Mà \(I\) là trung điểm của \(DE\), suy ra \(I\) là trung điểm của \(AM\). Vậy ba điểm \(A < I,M\) thẳng hàng.
c) Do \(ADME\) là hình chữ nhật nên \(DM//AC\). Suy ra \(\widehat {BMD} = \widehat {ACB}\) (hai góc so le trong). Mà \(\widehat {ABC} = \widehat {ACB} = 45^\circ \) (vì tam giác \(ABC\) vuông cân tại \(A\), suy ra \(\widehat {BMD} = \widehat {ABC} = 45^\circ \). Do đó, tam giác \(BDM\) cân tại \(D\). Suy ra \(BD = DM\).
Chu vi hình chữ nhật \(ADME\) là: \(2\left( {AD + DM} \right) = 2\left( {AD + BD} \right) = DM\)
Mà \(AB\) không đổi nên chu vi của tứ giác \(ADME\) không đổi.
d)
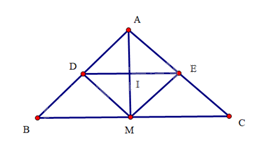
Do \(ADME\) là hình chữ nhật nên \(AM = DE\)
Suy ra \(DE\) có độ dài nhỏ nhất khi \(AM\) có độ dài nhỏ nhất. vậy \(M\) là hình chiếu của \(A\) trên đường thẳng \(BC\).
Trong tam giác \(ABC\) vuông cân tại \(A\) ta cóL
\(AC = AB = 2cm\) và \(B{C^2} = A{B^2} + A{C^2} = 8\)
Suy ra \(BC = \sqrt 8 cm\)
\(\Delta ABM = \Delta ACM\) (cạnh góc vuông – góc nhọn). Suy ra \(BM = CM = \frac{{BC}}{2} = \sqrt 2 cm\)
Tam giác \(ABM\) vuông tại \(M\) có \(\widehat {ABM} = 45^\circ \) nên \(\widehat {BAM} = \widehat {ABM} = 45^\circ \). Suy ra tam giác \(ABM\) vuông cân tại \(M\). Do đó \(AM = BM = \sqrt 2 cm\). Vậy \(DE = \sqrt 2 cm\).
Bài 25 trang 97 sách bài tập Toán 8 - Cánh Diều thuộc chương trình học Toán 8, tập trung vào việc ôn tập và củng cố kiến thức về các dạng bài tập liên quan đến hình học, cụ thể là các bài toán về tứ giác. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học về tính chất của các loại tứ giác (hình bình hành, hình chữ nhật, hình thoi, hình vuông) để giải quyết các bài toán thực tế.
Bài 25 trang 97 sách bài tập Toán 8 - Cánh Diều thường bao gồm các dạng bài tập sau:
Để giải bài 25 trang 97 sách bài tập Toán 8 - Cánh Diều một cách hiệu quả, bạn cần nắm vững các kiến thức sau:
Bài tập: Cho tứ giác ABCD có AB = 4cm, BC = 6cm, CD = 4cm, DA = 6cm. Chứng minh rằng ABCD là hình bình hành.
Giải:
Xét tứ giác ABCD, ta có:
Vậy, tứ giác ABCD có các cặp cạnh đối diện song song nên ABCD là hình bình hành (dấu hiệu nhận biết hình bình hành).
Khi giải bài tập về tứ giác, bạn cần lưu ý những điều sau:
Để học tốt môn Toán 8, bạn có thể tham khảo các tài liệu sau:
Bài 25 trang 97 sách bài tập Toán 8 - Cánh Diều là một bài tập quan trọng giúp bạn củng cố kiến thức về tứ giác. Hy vọng với hướng dẫn chi tiết và các ví dụ minh họa trên, bạn sẽ giải bài tập này một cách dễ dàng và hiệu quả. Chúc bạn học tốt!