Bài 27 trang 99 sách bài tập Toán 8 Cánh Diều là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về các định lý, tính chất của hình học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 27 trang 99 sách bài tập Toán 8 Cánh Diều, giúp các em học sinh hiểu rõ bản chất của bài toán và tự tin làm bài.
Cho một hình thoi có độ dài hai đường chéo là (frac{{18}}{5}) m và (frac{{27}}{{10}}) m. Tính chu vi và diện tích của hình thoi đó.
Đề bài
Cho một hình thoi có độ dài hai đường chéo là \(\frac{{18}}{5}\) m và \(\frac{{27}}{{10}}\) m. Tính chu vi và diện tích của hình thoi đó.
Phương pháp giải - Xem chi tiết
Dựa vào tính chất của hình thoi:
Trong một hình thoi:
- Các cạnh đối song song
- Các góc đối bằng nhau
- Hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường
- Hai đường chéo là các đường phân giác của các góc ở đỉnh.
Và dựa vào định lí Pythagore: trong một tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
Lời giải chi tiết
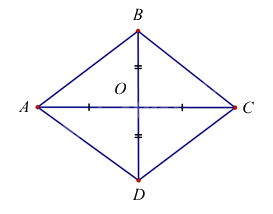
Xét hình thoi \(ABCD\) có \(AC = \frac{{18}}{5}m\), \(BD = \frac{{27}}{{10}}m\).
Gọi \(O\) là giao điểm của hai đường chéo \(AC\) và \(BD\).
Do \(ABCD\) là hình thoi nên \(AC \bot BD,O\) là trung điểm của \(AC\) và \(BD\).
Ta tính được:
\(OA = \frac{{AC}}{2} = \frac{9}{5}m\)
\(OB = \frac{{BD}}{2} = \frac{{27}}{{20}}m\).
Trong tam giác \(OAB\) vuông tại \(O\), ta có: \(A{B^2} = O{A^2} + O{B^2}\). Suy ra \(AB = \frac{9}{4}m\)
Chu vi của hình thoi \(ABCD\) là: \(4.\frac{9}{4} = 9\left( m \right)\)
Diện tích của hình thoi \(ABCD\) là: \(\frac{1}{2}.\frac{{18}}{5}.\frac{{27}}{{10}} = \frac{{243}}{{50}}\left( {{m^2}} \right)\).
Bài 27 trang 99 sách bài tập Toán 8 Cánh Diều thuộc chương trình học về tứ giác. Để giải bài tập này, học sinh cần nắm vững các kiến thức sau:
Bài tập 27 thường yêu cầu học sinh:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ đi vào giải chi tiết từng phần của bài tập. (Lưu ý: Nội dung giải chi tiết sẽ được trình bày cụ thể cho từng câu hỏi trong bài tập 27, giả sử bài tập có nhiều câu hỏi. Ví dụ dưới đây chỉ mang tính minh họa)
Cho tứ giác ABCD có góc A = 80 độ, góc B = 100 độ, góc C = 120 độ. Tính góc D.
Giải:
Áp dụng tính chất tổng các góc trong một tứ giác, ta có:
Góc A + Góc B + Góc C + Góc D = 360 độ
80 độ + 100 độ + 120 độ + Góc D = 360 độ
Góc D = 360 độ - (80 độ + 100 độ + 120 độ)
Góc D = 60 độ
Vậy, góc D của tứ giác ABCD bằng 60 độ.
Ngoài bài tập 27, các em học sinh có thể gặp các bài tập tương tự về tứ giác. Để giải quyết các bài tập này, các em cần:
Để củng cố kiến thức và kỹ năng giải bài tập về tứ giác, các em học sinh nên luyện tập thêm các bài tập khác trong sách bài tập và các tài liệu tham khảo. Giaitoan.edu.vn sẽ cung cấp thêm nhiều bài tập và lời giải chi tiết trong các bài viết tiếp theo.
Bài 27 trang 99 sách bài tập Toán 8 Cánh Diều là một bài tập quan trọng giúp các em học sinh hiểu rõ hơn về tứ giác và các tính chất của nó. Hy vọng với lời giải chi tiết và các phương pháp giải được trình bày trong bài viết này, các em học sinh sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn Toán.
| Khái niệm | Định nghĩa |
|---|---|
| Tứ giác | Hình có bốn cạnh |
| Tứ giác lồi | Tứ giác mà tất cả các góc trong đều nhỏ hơn 180 độ |
| Tứ giác lõm | Tứ giác có ít nhất một góc trong lớn hơn 180 độ |