Chào mừng các em học sinh đến với lời giải chi tiết bài 6 trang 60 sách bài tập Toán 8 Cánh Diều. Bài viết này sẽ cung cấp đáp án, phương pháp giải và giải thích rõ ràng từng bước để giúp các em hiểu bài và làm bài tập một cách hiệu quả.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán, cung cấp tài liệu học tập chất lượng và hỗ trợ giải đáp mọi thắc mắc.
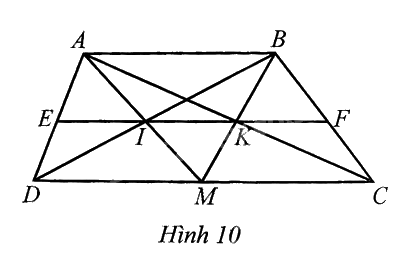
Trong Hình 10, cho biết \(ABCD\) là hình thang, \(AB//CD\left( {AB < CD} \right)\); \(M\) là trung điểm của \(DC\); \(AM\) cắt \(BD\) ở \(I\); \(BM\) cắt \(AC\) ở \(K\); \(IK\) cắt \(AD,BC\) lần lượt ở \(E,F\). Chứng minh:
Đề bài
Trong Hình 10, cho biết \(ABCD\) là hình thang, \(AB//CD\left( {AB < CD} \right)\); \(M\) là trung điểm của \(DC\); \(AM\) cắt \(BD\) ở \(I\); \(BM\) cắt \(AC\) ở \(K\); \(IK\) cắt \(AD,BC\) lần lượt ở \(E,F\). Chứng minh:
a) \(IK//AB\)
b) \(EI = IK = KF\)
Phương pháp giải - Xem chi tiết
Dựa vào định lí Thales: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
Lời giải chi tiết
a) Do \(DM//AB\) nên \(\frac{{IM}}{{IA}} = \frac{{DM}}{{AB}} = \frac{{MC}}{{AB}}\) (1) (do \(DM = MC\)).
Mặt khác, do \(MC//AB\) nên \(\frac{{MK}}{{KB}} = \frac{{MC}}{{AB}}\) (2)
Từ (1) và (2) suy ra \(\frac{{IM}}{{IA}} = \frac{{MK}}{{KB}}\)
Vì thế \(IK//AB\) (định lí Thales đảo)
b) Áp dụng định lí Thales lần lượt cho các tam giác \(ADM\) với \(EI//DM\), tam giác \(MAB\) với \(IK//AB\) và tam giác \(BMC\) với \(KF//MC\), ta có:
\(\frac{{EI}}{{DM}} = \frac{{AI}}{{AM}} = \frac{{BK}}{{BM}} = \frac{{KF}}{{MC}}\)
Suy ra \(EI = KF\) (do \(DM = MC\)). Mặt khác, áp dụng định lí Thales lần lượt cho các tam giác \(ADM\) với \(EI//DM\) và tam giác \(AMC\) với \(IK//MC\), ta có:
\(\frac{{EI}}{{DM}} = \frac{{AI}}{{AM}} = \frac{{IK}}{{MC}}\)
Suy ra \(EI = IK\) (do \(DM = MC\)). Do \(EI = KF\) và \(EI = IK\) nên \(EI = IK = KF\).
Bài 6 trang 60 sách bài tập Toán 8 Cánh Diều thuộc chương trình học Toán 8, tập trung vào việc ôn tập và củng cố kiến thức về các phép biến đổi đại số, đặc biệt là các biểu thức chứa biến. Mục tiêu chính của bài tập là giúp học sinh rèn luyện kỹ năng biến đổi biểu thức, rút gọn biểu thức và giải các bài toán liên quan đến biểu thức đại số.
Bài 6 bao gồm một số câu hỏi và bài tập khác nhau, yêu cầu học sinh thực hiện các thao tác sau:
Đề bài: Rút gọn biểu thức: (x + 2)(x - 2) + (x - 1)^2
Giải:
Đề bài: Tìm giá trị của biểu thức: 3x^2 - 5x + 2 khi x = -1
Giải:
Thay x = -1 vào biểu thức: 3(-1)^2 - 5(-1) + 2 = 3(1) + 5 + 2 = 3 + 5 + 2 = 10
Vậy, giá trị của biểu thức 3x^2 - 5x + 2 khi x = -1 là 10.
Đề bài: Chứng minh đẳng thức: (x + y)^2 - (x - y)^2 = 4xy
Giải:
Hy vọng với lời giải chi tiết và hướng dẫn giải bài tập trên, các em học sinh đã hiểu rõ cách giải bài 6 trang 60 sách bài tập Toán 8 Cánh Diều. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!