Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 8. Bài viết này sẽ hướng dẫn bạn giải bài 14 trang 55 sách bài tập Toán 8 Cánh Diều một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, đặc biệt là với những bài tập đòi hỏi sự tư duy và vận dụng kiến thức. Vì vậy, chúng tôi luôn cố gắng cung cấp những lời giải rõ ràng, chi tiết, kèm theo các giải thích cụ thể để bạn có thể hiểu rõ bản chất của bài toán.
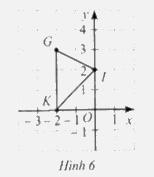
Cho tam giác \(GIK\) như Hình 6.
Đề bài
Cho tam giác \(GIK\) như Hình 6.
a) Xác định tọa độ các điểm \(G,I,K\)
b) Xác định tọa độ điểm \(H\) để tứ giác \(KOIH\) là hình vuông
c) Ba điểm \(G,H,K\) có thẳng hàng hay không? Vì sao?
d) Tính tỉ số \(\frac{{GH}}{{HK}}\)
Phương pháp giải - Xem chi tiết
Áp dụng cách xác định tọa độ các điểm trên mặt phẳng tọa độ để trả lời các câu hỏi.
Lời giải chi tiết
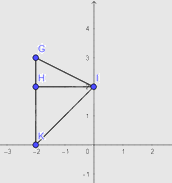
Ta vẽ điểm \(H\) như Hình.
a) \(G\left( { - 2;3} \right),I\left( {0;2} \right),K\left( { - 2;0} \right)\)
b) \(H\left( { - 2;2} \right)\)
c) Ba điểm \(G,H,K\) thẳng hàng vì ba điểm đều thuộc đường thẳng đi qua điểm -2 trên trục \(Ox\) và vuông góc với trục \(Ox\)
d) Ta có: \(\frac{{GH}}{{HK}} = \frac{1}{2}\)
Bài 14 trang 55 sách bài tập Toán 8 Cánh Diều thuộc chương trình học Toán 8, tập trung vào việc vận dụng các kiến thức về hình học, cụ thể là các tính chất của hình thang cân. Bài tập này yêu cầu học sinh phải hiểu rõ các định nghĩa, định lý liên quan đến hình thang cân, cũng như khả năng áp dụng chúng vào giải quyết các bài toán thực tế.
Bài 14 trang 55 sách bài tập Toán 8 Cánh Diều thường bao gồm các dạng bài tập sau:
Để giúp bạn giải bài 14 trang 55 sách bài tập Toán 8 Cánh Diều một cách dễ dàng, chúng tôi sẽ cung cấp lời giải chi tiết cho từng phần của bài tập. Dưới đây là hướng dẫn giải:
Để chứng minh một tứ giác là hình thang cân, bạn cần chứng minh:
Ví dụ, nếu đề bài yêu cầu chứng minh tứ giác ABCD là hình thang cân, bạn cần chứng minh AB // CD và AD = BC.
Khi đã chứng minh được một hình là hình thang cân, bạn có thể sử dụng các tính chất sau để tính toán:
Ví dụ, nếu bạn cần tính độ dài cạnh AD của hình thang cân ABCD, bạn có thể sử dụng định lý Pitago hoặc các tam giác đồng dạng.
Khi giải các bài toán thực tế, bạn cần:
Để giải bài tập hình thang cân một cách hiệu quả, bạn có thể áp dụng một số mẹo sau:
Để học tập và ôn luyện kiến thức về hình thang cân, bạn có thể tham khảo các tài liệu sau:
Hy vọng rằng với lời giải chi tiết và các mẹo giải bài tập mà chúng tôi đã cung cấp, bạn sẽ có thể giải bài 14 trang 55 sách bài tập Toán 8 Cánh Diều một cách dễ dàng và hiệu quả. Chúc bạn học tập tốt!